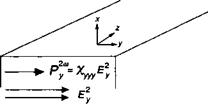
Режим с входящей ТЕ-модой и выходящей ТЕ-модой
В этом случае будем предполагать, что одиночная волноводная ТЕ-волна взаимодействует сама с собой таким образом, что амплитуда дается соотношением:
Я™ (*, ^ 0= - [л;{7.)е;{х)^(м-^) + к. С.] (9.В.2)
2
Здесь: Еесть решение волноводного уравнения (9.13), А®(?) учитывает изменение амплитуды пучка накачки (с частотой со) вдоль волновода, а ТЕ есть константа распространения 77:-волны с частотой со в волноводе, определяемая решением (9.13). При устранении членов по со — со (что соответствует оптическому выпрямлению) нелинейная поляризация на частоте 2со в (9.В.1) принимает вид:
(*> г, /)= -[/»ДГ(х, г)е-фм-2^"г) + к. с.] (9.В. Зл)
2
С использованием (9.В.2) получаем:
/£(*, г)= е^[А;(г)£;(х)]2 (9.В.36)
Анализируя следствия, которые влечет за собой введение нелинейной поляризации в уравнение связанных мод (9.23), мы видим, что член источника 2со обуславливает генерацию волн с частотой 2со. Уравнение (9.39) позволяет рассчитать изменение амплитуды волны 2со в волноводе. При рассмотрении только тех волн, которые распространяются направо, формула (9.39) приобретает вид:
- — - к. с. =
^ (9.В.4)
=----- -{еа%Г(х) к(^;(х)]2е'(2“'-2/,-™г) + к. с)Е^{х)йх
2сор0 Эг2 12
|
|
Рис. 9.В.1. Конфигурация генерации второй гармонизации ТЕ—ТЕ.
Здесь Р2(о ТЕ есть константа распространения волны 2со в волноводе. Используя обозначение для эффективного коэффициента преломления, мы видим, что Pico, те =ncfr(2co)2co /с. Е2а}(х) есть волноводная мода на частоте 2со. Функция f(x) представляет изменение нелинейной восприимчивости по всему волноводу. Например, в том случае, когда нелинейным является только материал сердцевины, f{x) является ступенчатой функцией. В этом случае уравнение (9.В.4) приобретает упрощенный вид:
|
Dz Р* |
(9.В.5)
Здесь: Буу есть интеграл перекрытия мод Еу с самими собой, определяемый формулой:
|
|
(9.В.6)
В то же время S/3 представляет собой рассогласование фаз:
|
(9.В.7) |
![]() TI: а. ТЕ ~ ^ [Weff (^®) Ис«Г (®)]
TI: а. ТЕ ~ ^ [Weff (^®) Ис«Г (®)]
![]()
|
ISPL |
![]() Уравнение (9.В.5) описывает перенос энергии между фундаментальной волной и ее гармониками. Для упрощения предстоящего обсуждения предположим, что эффективность преобразования мала. Тогда можно предполагать, что амплитуда А (у} (г) постоянна поперек волновода и равна своей величине на входе волновода (А**). В этом случае уравнение (9. В.5) может быть проинтегрировано:
Уравнение (9.В.5) описывает перенос энергии между фундаментальной волной и ее гармониками. Для упрощения предстоящего обсуждения предположим, что эффективность преобразования мала. Тогда можно предполагать, что амплитуда А (у} (г) постоянна поперек волновода и равна своей величине на входе волновода (А**). В этом случае уравнение (9. В.5) может быть проинтегрировано:
Вспоминая, что условия нормировки (9.20)—(9.22) устанавливают, что квадрат модуля амплитуды А2 мод в волноводе есть ничто иное, как мощность излучения, введенного в моду на единицу ширины волновода, мы получаем эффективность преобразования в волноводе в виде:
(9.В.9)
|
|
|
Я |
![]()
|
(9.В.10) |
![]()
|
Рт 4 [/?cff (2 со ) - ле|Г (a )J |
![]()
|
Длина согласования фаз в волноводе Эта величина возрастает (так же, как и максимальная эффективность) по мере уменьшения дисперсии волновода. Позже мы увидим, что для искусственного получения согласования фаз могут быть использованы определенные методы. В этом случае функция главного синуса (sine) в (9.В.9) равна единице, при этом преобразование частоты может происходить конструктивно по всей длине волновода, что приводит к параболической зависимости (по L2) эффективности преобразования. Теперь мы придадим более физический вид выражению (9. В.9). Для этого мы должны рассчитать интеграл перекрытия S. С этой целью сделаем несколько упрощающих аппроксимаций: |
 В этой последней формуле уровни мощности Р выражены в Вт на единицу ширины волновода. Рассмотрим изменение эффективности преобразования по длине волновода Ь. Нелинейная среда извлекает энергию из пучка накачки и передает ее второй гармонике, при этом периодически по длине волновода имеет место обратный процесс. В результате этого максимально достижимая эффективность достигается на конце длины взаимодействия, которую называют (правда, не совсем уместно) длиной когерентности и которую мы называем длиной согласования фаз:
В этой последней формуле уровни мощности Р выражены в Вт на единицу ширины волновода. Рассмотрим изменение эффективности преобразования по длине волновода Ь. Нелинейная среда извлекает энергию из пучка накачки и передает ее второй гармонике, при этом периодически по длине волновода имеет место обратный процесс. В результате этого максимально достижимая эффективность достигается на конце длины взаимодействия, которую называют (правда, не совсем уместно) длиной когерентности и которую мы называем длиной согласования фаз:
• Только материал сердцевины является нелинейным, а функция Дх) является ступенчатой.
• Волноводы являются бесконечно ограничивающими, а моды — синусоидальными, как в (9.23), т. е.:
|
(9.В.12 я) (9.В.126) (2*у). Подставляя это последнее уравнение в (9.В.9), мы, в конце концов, получаем величину эффективности преобразования частоты для абсолютно ограничивающего нелинейного волновода для случая без обеднения пучка накачки (т. е. для Аш = const): |
|
-2 № ь |
|
-ilЈE>PoSin™ dpm d |
|
Е:{х) |
|
(9.В.11) |
|
Ґ 32 л2 |
|
І мГро3 |
|
С2 _ Ьуу - |
|
Зл - |
|
В этом случае интеграл перекрытия может быть записан в виде: Х чЗ/2 . <1 |
|
32 VI 1 (юЦоРоУ |
|
/2 |
|
Н?>- |
|
1 |
|
S„= 8V2 |
|
Зл 4d рв№ |
|
РЖІ2 |
|
Или: |
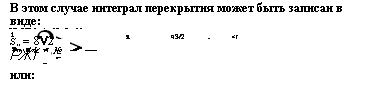 |
|
|
|
{(оед^ь)2 |
|
S0L) |
|
Sm с4 |
|
Dl |
|
Ру1т(Й |
|
/і со П |
|
||
|
||
Эффективность преобразования в нелинейном волноводе
Здесь: Z0 есть вакуумный импеданс величиной 377 Ом. Обратите внимание! В последнем уравнении уровни мощности Р выражены в Вт м-1 по ширине волновода, а / есть ширина волновода. В случае согласования фаз эффективность преобразования определяется соотношением:
|
(L) |
|
D 2а> У |
|
= 4,3x10' |
|
|||||||
|
|||||||
Это уравнение вскрывает существенное препятствие (порядка 10~20 для типичных значений %2(0 и уровней мощности) для достижения разумного значения эффективности и одновременно объясняет привлекательность волноводов с точки зрения их использования при преобразовании частоты. Благодаря оптическому ограничению в волноводах электромагнитные поля могут быть значительными даже при сравнительно невысоких уровнях мощности, что приводит к осязаемой эффективности преобразования.
Пример--------------------------------------------------------------------------------------------------------------
Предполагая, что задача согласования фаз решена, рассмотрим волновод на основе ОаАБ (х2 * 100 пм В-1 и пе№ * 3) длиной 2 мм, толщиной 0,5 мкм и шириной 2 мкм. При введении в волновод оптического излучения мощностью 10 мВт на длине волны Л0 = 2 мкм эффективность преобразования составит:
4,3х Ю"20 (2х 10+3 мкм/2 мкм)(ю2 пм В"1)(ю-2 Вт/(0,5х 10-6 х м2 ))/33, т. е.16%
Квазифазовое согласование
Мы видели, что условия согласования по фазе выполняются, когда есть дисперсия между волной накачки на частоте со и гармоникой на частоте 2со (т. е. Рсо * Р2(о).
Однако, мы знаем, что в полупроводниках зонная структура приводит к существенной дисперсии и что эта дисперсия существенно усиливается в волноводах (смотрите рис. 9.7). Могло бы показаться, что согласование фаз по своей природе невозможно в объемных полупроводниках. Однако, как оказывается, можно прибегнуть к услугам технологии, чтобы пространственно свойства этих материалов могли бы достичь такого состояния, которое называется квазифазовым согласованием.
|
Л |
![]() При первом интуитивном подходе предположим, что мы можем модулировать величину нелинейной восприимчивости периодическим образом вдоль волновода:
При первом интуитивном подходе предположим, что мы можем модулировать величину нелинейной восприимчивости периодическим образом вдоль волновода:
(2 к
Л ^ (9.В.14)
В этом случае уравнение связанных мод (9.В.4) изменяется незначительно: член в экспоненте под знаком интеграла становится равным i2cot — (2ТЕ ± 2/Л)г). При этом
Все теоретические выкладки для эффективности преобразования остаются прежни
Ми за исключением того, что член фазового рассогласования становится равным:
# = А». ТЕ - 2А, ТЕ ±— (9. В. 15)
Л
Условие, приводящее к квазифазовому согласованию может быть записано в виде:
Л
Условие квазифазового согласования
Рисунок 9.В.2 дает интерпретацию этого условия. Волновой вектор решетки (2я/А) добавляет к этому волну накачки, что приводит к эквивалентности с волновым вектором гармоники.
|
У2& ж— 2 у2й} 2о) _ Лууу ^Лууу • ^«-"2 4- пп 1 П нечетное |
![]() С технологической точки зрения это может быть осуществлено за счет использования пространственного разрушения оптической нелинейности периодическим образом с использованием ионной имплантации, методов кристаллического роста, примесной диффузии и т. д. В этом случае выражение для нелинейности может быть записано в следующем виде:
С технологической точки зрения это может быть осуществлено за счет использования пространственного разрушения оптической нелинейности периодическим образом с использованием ионной имплантации, методов кристаллического роста, примесной диффузии и т. д. В этом случае выражение для нелинейности может быть записано в следующем виде:
-^*1 (9.В.17)
Л )
В уравнении связанных мод (9.В.4) лишь один член, соответствующий условию квазифазового согласования будет давать ненулевой вклад:
(9.В.18)
А
Таким образом, фазовое согласование может быть получено при длине гофра, равной А (п = 1, первый порядок), ЗА (п = 3, третий порядок) и т. д. Очень простой расчет показывает, что для фазового согласования первого порядка эффективность преобразования частоты остается той же самой, что величина, определяемая (9.В.13я):
ТЕ ТЕ
^2о>,ТЕ
Рис. 9.В.2. Интерпретация условий квазисогласования фазы с использованием вол - 2л
Новых векторов. Д
|
|
|
|
Гофрирование, обеспечивающее фазовое согласование более высокого порядка, приводит к еще меньшей эффективной нелинейной восприимчивости.
Рисунок 9.В. З. иллюстрирует физический принцип, лежащий в основе квази - фазового согласования. В пределах последовательных интервалов, каждый из которых перекрывает Лрт, нелинейные диполи устраняются, при этом подавляется механизм, ответственный за деструктивную интерференцию.
|
|
|
|
|
К ^ /' : /Т |
1 1 1 1 1 Без фазового согласования / і / і |
|
|
/ 1 / 1 / 1 / і і |
||
|
Длина когерентности ; < ►: |
Г расстояние і і • |
|
|
Х2 Х2 |
Хг |
|
|
Рис. 9.В. З. Метод квазифазового согласования для оптического преобразования частоты в нелинейном волноводе. Оптическая нелинейность попеременно устраняется или оставляется неизменной в пределах последовательных интервалов, каждый из которых перекрывает одну длину когерентности. |