Оптоэлектроника

Распределение носителей В фотовозбужденном полупроводнике

Сложность механизмов фотовозбуждения обусловлена множеством различных ха­рактеристических длин, управляющих электрон-фотонным взаимодействием в сре­де. Во-первых, эти процессы зависят от глубины поглощения, которая по порядку величины составляет несколько а~1 (смотрите разделы 7.3 и 7.4). Затем, важную роль играют диффузионные длины неосновных носителей (глава 10), определяю­щие расстояние, на котором носители эффективно участвуют в механизмах детек­тирования. И, наконец, есть еще и размеры области пространственного заряда, имеющие особое значение в фотовольтаических приемниках. Все эти характерис­тические длины имеют практически тот же порядок величины — от нескольких микрометров до нескольких десятков микрометров. Таким образом, ни одним из этих механизмов нельзя пренебрегать в пользу каких-либо других. В большинстве случаев для описания механизмов детектирования необходимо прибегать к полным уравнениям для полупроводников (уравнения (6.60) и (6.61)). В этом разделе мы опишем эти уравнения, не прибегая к их решению во всей их полноте — такая работа была бы возможна, но утомительна и привела бы к результатам ограничен­ной полезности. В то же время они будут полезны для читателя при условии их соответствующего упрощения применительно к особенностям решаемой задачи. Мы ограничимся одномерной трактовкой (вдоль оси Ог распространения света) и пренебрежем проблемами, возникающими из-за неоднородной засветки и т. д.

Для начала отметим, что световой поток в среде убывает экспоненциально в соответствии с соотношением:

Ф(*)=Ф0е-аг (ил)

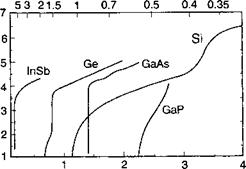
Здесь Ф0 есть поток фотонов, падающий на поверхность. В свою очередь, коэффи­циент поглощения является функцией энергии фотонов, как это уже объяснялось в главах 7 и 8. Рисунок 11.2 демонстрирует спектральные зависимости коэффициента поглощения а (И у) для ряда полупроводников, имеющих особое значение для опто­электроники. Отметим различный характер спектральной зависимости а (Ну) для прямозонных (ваАБ, 1пА$, 1п5Ь) и непрямозонных полупроводников подобно 51, ко­торый проявляет менее резкий край оптического поглощения по сравнению с пря­мозонными материалами.

Длина волны (мкм)

Фотоны, поглощенные полупроводниками, генерируют электронно-дырочные пары с концентрацией Ап = п — п0и Ар = р — р0 при скорости генерации, определя­емой соотношением:

(11.2)

После рождения носители заряда ожидают два варианта дальнейшего развития событий. Либо они рекомбинируют друг с другом с характеристическим временем жизни г (г для электронов и г для дырок), либо они будут удалены электрическим

Полем или диффузией к омическим контактам. Уравнения (6.60) и (6.61), которые

Описывают эти механизмы, имеют вид:

(МЛ

Здесь плотности тока электронов (У) и дырок (/) составляют:

— = Оп—п + п/лЕ (11.4а)

Я Эг

— = - й -^-Р + РМ, Е (Н.46)

Я Ъг

При этом коэффициенты /1И О есть подвижности и коэффициенты диффузии для соответствующих типов носителей. В таблице 1.1. приведены характеристики переноса этих материалов, а именно: типичные рекомбинационные времена жизни (которые, естественно, могут зависеть от засветки), подвижности, значения шири­ны запрещенной зоны и диэлектрические постоянные.

К этим уравнениям мы должны добавить уравнение Пуассона, позволяющее нам рассчитать электрическое поле в функции постоянной плотности заряда, обус­ловленного легирующими примесями, а также концентрации фотогенерированных носителей, т. е.:

^=7 (/»+*;-"-*;) (11.5)

Здесь е есть диэлектрическая постоянная материала (при этом £ = е0£г, а ег — отно­сительная диэлектрическая проницаемость), а И/ и УУ“ есть концентрации легиру-

Ющих примесей. В состоянии равновесия (т. е. в отсутствие засветки) и в объеме материала И/ + р0 = N “ + п0.

Уравнение (11.5) позволяет понять, каким образом эффективность фотодетек­тирования фотодиода изменяется при больших уровнях засветки, когда, например, Ал ~ Л^. Важно отметить, что характеристическое время, называемое диэлектричес­ким временем релаксации, в течение которого материал сохраняет электрическую нейтральность, достаточно мало (г1.с1 = е/а « 10“12 с, где а есть проводимость мате­риала). Таким образом, среда будет электрически нейтральной, т. е.:

Д«(г, г)= ДР(г, 0

Последнее уравнение, несмотря на свой простой вид, имеет очень важные след­ствия с точки зрения динамики фотоприемника. Во-первых, поскольку носители рекомбинируют парно, это означает, что рекомбинационные времена должны быть равными (г = г = т). В свою очередь, это возможно только, если механизмы зави­сят тем или иным образом от п и р. Другим следствием равенства (11.6) является то, что внутреннее поле должно установиться прежде, чем это условие может быть наложено на (11.3), (11,4) и (11.5). Мы могли бы еще более усложнить приведенную выше таблицу за счет введения механизмов захвата для каждого типа носителей, пространственной неоднородности и т. д.

Начнем с упрощения системы, которую пытаемся исследовать. Предположим, что материал фотоприемника имеет преимущественно р-тип проводимости (р » р0, при этом, как мы увидим дальше, этот случай представляет интерес с прикладной точки зрения), а также то, что не прикладывается никакое электрическое поле Е(г)- Мы всегда можем пренебречь всеми эффектами, связанными с сохранением нейт­ральности заряда, как, например, возникновением внутреннего поля — эта нейт­ральность гарантируется основной легирующей примесью. Подставляя (11.4д) в (11.3л), мы получаем:

(11.7)

Решением этого уравнения является сумма частных решений, включая член источника, а также общее решение без члена источника, т. е.:

(11.8)

Здесь: Ь0 есть диффузионная длина электронов Ь0 = л/(/)т), а константы Ли В определяются граничными условиями, специфичными для каждой определенной задачи. Эти условия могут быть нескольких типов:

Поверхностная рекомбинация Б (в единицах см с“1) при I = накладывает условие:

(119)

Омический контакт, т. е. граница раздела, где рекомбинация неосновных носи­телей заряда мгновенна (омический р+ контакт к материалу р-типа накладывает усло­вие на концентрацию неосновных носителей п в виде пр = я.2, т. е. п ~ 0) так, что:

Д« и.=0

Область пространственного заряда, начинающаяся при г — т. е. область, из которой удаляются все носители, вновь приводит к:

Проанализируем, например, случай с бесконечно толстым образцом (с1» ьви1 /а). Когда I —> °°, Ая —> 0. Коэффициент А в этом случае получается с использованием граничных условий при I = 0. Предположим, что омический контакт отсутствует и электроны могут свободно рекомбинировать на поверхности (I = 0) со скоростью 50. Уравнения (11.8) и (11.9) сразу дают распределение фотогенерированных носи­телей А я(г):

(11.11)

Как можно было бы ожидать, концентрация носителей на поверхности стано­вится нулевой при скорости рекомбинации, стремящейся к бесконечности (смот­рите рис. 11.3). Если, с другой стороны, поверхность полупроводника пассивирова­на (т. е. плотность поверхностных состояний равна нулю), то 50 = 0 и количество носителей, генерированных во всем объеме, дается интегралом (11.11):

Последнее выражение можно прочитать как Апм/т= Ф0, т. е. полный поток падаю­щих фотонов Р0 преобразуется в поток носителей Ап1о1/т.

О

5

10 15

Расстояние (мкм)

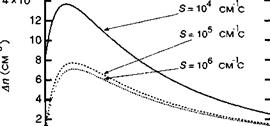
Рис. 11.3. Распределение фотогенерированных носителей при потоке фотонов

Ф0 = 1018 см-2, коэффициенте диффузии 1 см2 с-1, диффузионной длине 10 мкм и коэффициенте поглощения 104 см-1, а также для различных значений ско­рости поверхностной рекомбинации 5.

Другой очень простой случай связан с рассмотрением образца толщиной */, по которому ток не может протекать через поверхности входа и выхода излучения (например, это фотопроводник, в котором направление распространения элект­рического тока перпендикулярно потоку фотонов): в предположении отсутствия внеш­него электрического поля это означает, что / = ВпдАп /дг — 0 при I = 0 и при z-d. Интегрирование (11.7) немедленно приводит к полной поверхностной концентра­ции фотоносителей Апш, генерированных в объеме:

(11.13)

Отношение потока генерированных носителей Ая1о1/ги потока падающих фото­нов Ф0 выражает эффективность преобразования потока фотонов в поток носите­лей. Этот отношение есть внутренняя квантовая эффективность г], фотоприемника, которая в данном случае определяется выражением:

Г), = = -е-ы (11.14а)

Фо

Внутренняя квантовая эффективность фотоприемника

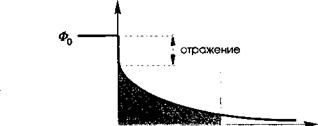
Одновременно с внутренней квантовой эффективностью должны быть учтены и потери. Наиболее важные из них, как правило, связаны с потерями фотонов за счет оптического отражения ОТ поверхности, Т. е. 77ор = 1 — Я. Этот коэффициент оптической эффективности особенно мал в случае границы раздела необработанной полупроводниковой поверхности и воздуха, поскольку коэффициент преломления полупроводника п1с значителен, а Я = (п1с — 1)2/(«1с + I)2. Так, в случае пх = 3,4, что приводит к Я = 0,3 и /7ор = 1 — Я = 0,7. Таким образом, полная эффективность, как правило, близка к:

П = г, Лор = - е-°*) (11.146)

Для уменьшения потерь на отражение на границе раздела полупроводник/воз­дух в широком спектральном диапазоне часто используются антиотражающие по­крытия. Рисунок 11.4 суммирует различные факторы, влияющие на полную эффек­тивность фотоприемника.

Пример--------------------------------------------------------------------------------------------------------------

Найдем распределение носителей в полупроводнике с коэффициентом поглоще­ния аг= 104 см-1. Предположим также, что материал характеризуется подвижностью носителей 40 см2 В"1 с-1 и рекомбинационным временем жизни 10~6 с. Эти парамет­ры приводят к коэффициенту диффузии, определяемому соотношением Эйнштей­на Вп = (кТ/4)/гп величиной в 40 см2 В-1 с-1 х 25,9 мВ или 1 см2 с-1, при этом диффу­зионная длина (Впт)1/2 составляет 10 мкм. Таким образом, понятно, что в соотноше­нии (11.1) яг доминирует над 1/Ь, при этом распределение Ап($ прежде всего зависит от относительной величины и а. Рисунок 11.3 иллюстрирует распределения Адля различных значений скорости поверхностной рекомбинации £0.