Порог прозрачности
Рассмотрим р-п-диод с одиночной квантовой ямой (смотрите рис. 13.19). При прямом смещении этого диода инжектированные носители аккумулируются в квантовой яме. Концентрация носителей на единицу площади ns может быть получена по аналогии с (13.13), т. е.:
Ns = ps= ^2- (13.48)
Я
При достаточно большом токе мы получаем инверсию заселенности, что приводит к прозрачности квантовой ямы (смотрите рис. 13.20). В окрестности прозрачности квазиуровни Ферми начинают проникать в подзоны. При этом в процесс вовлечены только подзоны с п =т = 1, при этом усиление может быть записано просто в виде:
Y(hv)= a1Dfe(hv)- fy(hv)e{hv - Eg-et - hht) (13.49)
Оптическое усиление вследствие первого перехода е1 - hh.
~Fn
Fp
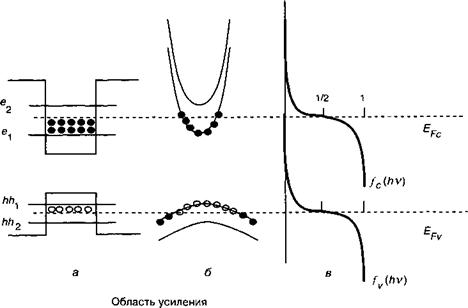
Рис. 13.19. Прямо смещенный р-п-диод с одиночной квантовой ямой.
|
|
|
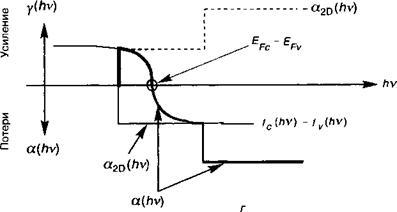
Рис. 13.20. По мере того, как квантовые ямы заполняются электронно-дырочными парами, квазиуровни Ферми поднимаются внутри подзон. Как только энергетический зазор между двумя квазиуровнями Ферми превысит ширину запрещенной зоны, фотоны, удовлетворяющие условию Бернара—Дюрра - фура, начинают усиливаться: зонная диаграмма (а), подзонная структура (б), соответствующие распределения Ферми—Дирака (в) и кривая усиления в квантовой яме (г). |
Понятно, что эффекты уширения могут быть учтены в виде свертки с использованием функции Лоренца:
П. = ]ргВ..(Я)/с'(Е)М
", = }ро,,(£)[! - Л(Е)]*Е
|
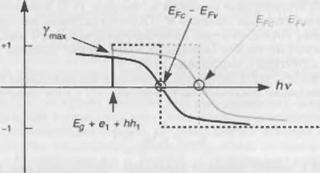
Мы увидим, что концентрации прозрачности и порога могут быть выражены в виде произведения этих двумерных критических концентраций на коэффициент, близкий к 1 (как правило, в интервале от 1 до 5). Такой метод расчета усиления заключается в следующем: при заданной плотности тока / мы находим концентрацию носителей, определяемую (13.48), затем определяем квазиуровни Ферми в соответствии с (13.53) и, наконец, с помощью (13.49) и функций Ферми (13.45) находим усиление. Рисунок 13.21 демонстрирует кривую усиления (13.48) в функции энергии фотонов при возрастающей концентрации носителей. Отметим резкое увеличение усиления при ку > Е + е{ + ккх. Такой характер является более резким по сравнению со случаем регулярного гетероперехода и он связан со ступенчатым профилем плотности состояний в двумерной структуре (в противоположность зависимости ^Е, проявляющейся в трехмерных структурах). Таким образом, максимальное усиление утйХ достигается, когда Ку = Е + е, + /*/*., т. е.: G 1 1 |
|
E. - e |
|
Пс = In |
|
1 + exp |
|
KT R hh{ - E Fv kT |
|
In |
|
1 + exp |
|
MckT лЛ2 |
|
"с = PlD. ekT = |
|
О кт - mhhkT H2D. hhn'i — |
|
Tltl |
|
Уравнения (13.53) и (13.45) позволяют простым образом связать величину функции Ферми с концентрацией носителей п: 1 |
|
1 6 1 1 + exp[(Јft - Et - ех)/кТ] f'(E>+e'} |
|
(13.56а) |
|
1 |
|
Я, = р™екТ ~u^+~u)du = АаД In |
|
(13.52) |
|
1 + |
|
1 |
|
”s = PlV. e J - F л. p 1 |
|
(13.51) |
|
D E |
|
L, 1 + exp [(f - Ef )/ kT ] |
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
|
|
|
 |
|
|
|
 |
|
|
|
|
|
 |
|
|
|
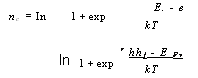Рис. 13.21. Изменение кривой усиления для квантово-размерного лазера при возрастающем уровне накачки. Пунктирные кривые показывают величну усиления при нулевой температуре. Жирная (слабая) линии соответствуют сильным (слабым) уровням накачки. |
Г - = «20 (1 - е-"'/л' - е(13.57)
Максимальное усиление квантовой ямы в функции концентрации носителей (см "1)
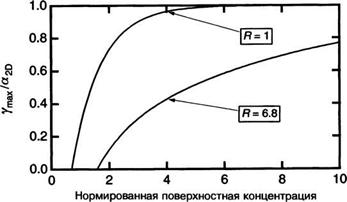
Здесь: Яс}> (= ткк/т) есть отношение эффективных масс носителей в зоне проводимости и валентной зоне. Рисунок 13.22 демонстрирует изменение максимального усиления в функции приведенной поверхностной концентрации п5/пс при Я = 6,8 (для СаАв) и Я = 1. Мы видим, что усиление быстро возрастает, как только достигается условие прозрачности, но оно быстро насыщается. Это происходит из-за двумерного характера состояний. Из (13.57) следует, что порог прозрачности достигается, как только максимальное усиление становится положительным, т. е. когда достигается порог прозрачности п1г:
Е-п«/пе + е= ! (13.58)
|
Рис. 13.22. Нормированное (по отношению к поглощению аю) усиление в функции нормированной (по отношению к двумерной критической концентрации носителей пс) поверхностной концентрации носителей. |
При Ясу = 1 мы имеем п1г = пс 1п(2). Ток прозрачности всегда связан с пс через численный коэффициент, близкий к 1. Это объясняет важность концепции двумерной критической концентрации носителей пс. Рисунок 13.22 демонстрирует условие прозрачности для различных значений Ясу. Отметим важность четкого согласования эффективных масс носителей в зоне проводимости и валентной зоне. Это и является одной из причин мотивации выращивать напряженные лазерные структуры (мы исследуем эти структуры в дополнении 13.Б).
Следует отметить, что в литературе изменение максимального усиления утах в функции концентрации носителей часто принимается в виде логарифмической зависимости:
(13.59)
Здесь константа у0 зависит только от отношения эффективных масс Ясу и получается процедурой подгонки (смотрите ниже). Эта последняя формула приводит к характеру поведения, близкому к предсказываемому формулой (13.57) для величин п, которые приближаются к порогу прозрачности. Это уравнение обладает тем преимуществом, что оно простым образом вводит порог прозрачности в формулу усиления. Заметьте отличие от подобного, но линейного соотношения (13.21) для трехмерных лазерных диодов.
Пример----------------------------------------------------------------------------------------------------------
1. Используем следующую программу МАНЕМАТ1СА для подтверждения эквивалентности (13.57) и (13.59):
Т=1-Ехр[-х] - Ехр[-х/Я]
13=6.8
Р1оМ =Р1оЩ, {х, .5,5} ]
ПпсИЗоо^ =0, {х, 1}] х0=х/.%
Рк*2=Рк*[0.48*д,{х,.5,5}]
8Иол/[р1о11,р1о12]
Рисунок 13.23 дает сравнение этих двух выражений. С использованием процедуры подгонки мы находим, что у0 = 0,48а2В.
2. В случае ваАв плотности двумерных состояний есть:
Рю. е = тс! лЬ1 - 2,8 х 1013 см"2 эВ-1 Аалл = Щи/лЬ2 = 1,9 хЮ14 см2 эВ'1
Критическая двумерная концентрация носителей в зоне проводимости есть пс = Рю или 2,8 х 1013 см~2 эВ1 х 0,0259 эВ =7,25 х 1011 см-2. Рисунок 13.22 показывает, что в GaAs ntr= 1,6 пс = 1,6 х 10 см-2. В квантовой яме толщиной 100 Е это соответствует пороговой концентрации прозрачности 1,16 х 10 см-3. Этот результат очень близок к тому, который получается для объемного материала. В действительности преимущество использования квантовых ям заключается не в уменьшении пороговой концентрации носителей, а скорее в уменьшении плотности тока прозрачности и, следовательно, в уменьшении пороговой плотности тока.
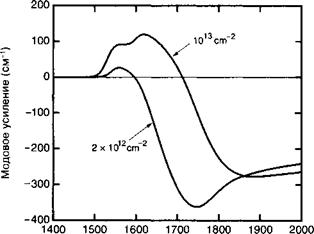
В действительности кривая усиления квантово-размерного лазера очень сложна. По мере того, как в квантовых ямах увеличиваются концентрации носителей, электроны и дырки начинают заселять все более высоко лежащие энергетические состояния в подзонах, что приводит сложным переходам: сначала к е— кк^переходам, затем к е2-кк2-переходам и т. д. Рисунок 13.24 показывает результаты расчета, учитывающего все эти переходы.
|
Энергия (мэВ) Рис. 13.24. Модовое усиление (т. е. произведение усиления на коэффициент ограничения Г) для квантово-размерного лазера при двух различных значениях концентрации носителей. В условиях более высоких уровней инжекции тока могут наблюдаться как так и е2-кк2-переходы (С разрешения А. РПу@ТНАЬЕ8) |
