Оптоэлектроника

Поглощение на свободных носителях

Одним из наиболее поразительных аспектов полупроводников является способ­ность их электронов либо поглощать, либо излучать свет в процессе челночных переходов между зоной проводимости и валентной зоной, которые обычно называ­ются межзонными переходами. В то же время существует другой тип оптических переходов с участием состояний в пределах одной зоны, называемых внутризонны - ми переходами.

Рассмотрим полупроводник с коэффициентом преломления пор (€0П 2ор = е). Поглощение, обусловленное свободными носителями учитывается электропро­водностью а. Пусть полупроводник находится под воздействием электромагнит­ной волны Е с частотой со, распространяющейся вдоль направления г и падающей на поверхность при г =0. Эта волна вызывает протекание в объеме электрическо­го тока с плотностью] = стЕ. В этой первой части предположим, что электропро­водность не зависит от частоты со. В полупроводнике электромагнитная волна

Является решением уравнений Максвелла (смотрите (2.1)):

V х В = ——

Аг (7.В.1)

УхЕ =

С! г

Где Б есть вектор смещения, связанный с электрическим полем Е и поляризацией Р соот­ношением:

Б = е0Е + Р = е0Е + е0^[11]Е = £Е (7.В.2)

Как мы уже видели в главе 2, система уравнений (7.В. 1) дополняется уравнением V • В = О, а также в предположении нейтральности среды — законом Пуассона V • Е = 0. При использовании (7.В.1), (7. В.2) и этих двух нулевых дивергенций уравнения Макс­велла приводят к простому волновому уравнению:

Г7 ~ I? СГЕ /*7 о ЛЧ

V Е = //0ст — + ]и0£—- (7.В. З)

<*>

Дисперсионное соотношение со(к), связывающее волновой вектор и частоту, может быть получено подстановкой волнового уравнения Е= Е^{а)1~к1) (7.В. З), что дает:

К2 = /и0есо2 - [со]и0о (7.В.4)

Таким образом, мы приходим к двум различным режимам, зависящим от относитель­ной амплитуды действительной и мнимой частей (7.В.4).

Сильная проводимость (а» есо)

В этом случае в (7.В.4) доминирует мнимая часть, при этом волновой вектор дается соотношением:

К2 -Асо/цр (7.В.5)

Мы видим также, что амплитуда волны уменьшается экспоненциально с коэффици­ентом поглощения, определяемым двойным корнем квадратным от (7.В.5). Величина, об­ратная этому коэффициенту, приводит к характеристической длине, называемой глубиной скин-эффекта 8, и она корректно отражает расстояние, на котором волна поглощается свободными носителями (рис. 7.В.1):

Скин слои

Кремний

Рис. 7.В.1. Под действием засветки пластина крепления становится сильнопроводя - щей и экранизирующей СВЧ-волну на глубину скин-слоя. Часть сигнала поглощается на этой глубине, а другая — отражается.

Пример

Предположим, что мы хотим сконструировать планарный отражатель для радара на основе кремния (е$. = 13), работающий в т. н. А'-полосе, т. е. в области 10 ГГц (смотрите рис. 7.В.1). В темновых условиях кремниевый обладает очень большим удельным сопротивлением (р > 1000 Ом см). В условиях засветки его проводимость резко возрастает. Неравенство а» ев) удовлетворяется, как только удельное со­противление установится меньше, чем 1/(2ях 1010 с-1 х 13 х 8,85 х 10-14 Ф см-1) или 14 Ом см. Такой величины легко добиться за счет засветки. Говоря более точно, давайте рассмотрим кремниевый слой (с подвижностью р = 1000 см2 В-1 с-1, време­нем жизни носителей г= 1 мс и толщиной 1 мкм), используемый в качестве отра­жающего слоя на частоте 10 ГГц. Во-первых, для того, чтобы отражать радарную волну эффективно, глубина скин-эффекга должна быть меньше толщины слоя крем­ния или а > 1/(2 х 1,2 х 10_6 Гн м-1 х 2жх х 10 с-1 х 10-12 м2), т. е. 6,6 х 106 Ом-1 м-1. Это удельное сопротивление соответствует концентрации фотогенерированных носите­лей п = а/до или 4 х 1020 электронов на см-3. Для этого, в свою очередь, требуется плотность мощности падающего излучения Р (= т//*г/г) на уровне 6,4 Вт см-2 для фотонов с энергией 1 эВ.

Слабая проводимость (а« есо)

В этом случае (7.В.4) приобретает вид:

(7.В.7)

Мы видим, что волна поглощается (£0е К1) и что ее интенсивность / ослабляется с константой ослабления аг(/0е~2,сг =

(7.В.8)

Где есть вакуумный импеданс (2^ = (р0/е^1/2 = 377 Ом). В действительности, в последнем выражении мало пользы, так как оно не учитывает динамики электро­нов, т. е. оно предполагает, что электропроводность является функцией мгновен­ной величины напряженности электрического поля, что, как правило, не имеет места. В связи с этим мы представим более корректную модель, которая учитывает время реакции электронного газа и которая называется моделью Друде.

Рассмотрим газ свободных электронов с концентрацией п, состоящий из элек­тронов с эффективной массой те[Г (смотрите главу 5). В главе 6 мы видели, что

Полная зонная структура материала может быть учтена с использованием понятия эффективной массы и что динамическое поведение электрона может быть описано уравнением:

= ЧЕ(іг) (7.В.9)

Где V есть скорость электрона, а т есть среднее время между столкновениями. Если приложенное поле постоянно £(/) = Е0, скорость также будет постоянной и опреде­ляемой соотношением у0 = qтE0/mefp при этом плотность электрического тока, возни­кающего из-за общего движения газа, составляет у0 = = сг0Е0. Таким образом,

Электропроводность составляет сг0 = пфт/т^ что является тем же результатом, кото­рый мы нашли уже ранее в разделе 6.2. Если поле является электромагнитным типа Е6Ш то в этом случае уравнение (7.В.9) показывает, что проводимость сг(со) зависит от частоты в соответствии с соотношением:

О(а)=-°[12]— (7. В. 10)

1 +1 т

Дисперсионное соотношение (7.В.4), описывающее связь между волновым век­тором к и частотой (о, остается действительным при замене а на приведенное выше выражение для а (со). Таким образом, мы сразу получаем выражение для поглоще­ния (более точное по сравнению с соотношением (7.В.8)):

« = --------- ^7%- (7.В.11)

Иор 1 + (сОТУ

Произведение Z0cг0 по размерности соответствует обратной длине. В кристалли­ческих полупроводниках, время столкновений, как правило, лежит в диапазоне 0,1—10 пс, и произведение (от составляет для оптического диапазона очень боль­шую величину. Таким образом, выражение (7.В.11) может быть упрощено до вида:

А= г0 пдг% (7.В. 12)

Аж пор т.„т

Модель Друде для поглощения на свободных носителях

Пример--------------------------------------------------------------------------------------------------------------

Брусок кремния (пор = 3,6, пгса= 0,321 т0) легирован до концентрации 1020 см-3 или 1026 м_3. При этом уровне легирования среднее время столкновений г составляет 10-14 с. Этот результат приводит к проводимости:

А0=!Н! і = 1.0:>^к6_х10^_к£І1|0^£ = 8,8Х10- 0м-< м-< ли 0,321 х 0,9 х 10-30 кг

Или удельная проводимость составляет величину порядка 1 м Ом см-1. Коэффици­ент поглощения излучения на длине волны 10 мкм (2 х 1014 с-1) дается (7.В. 11) и составляет:

А= г0о0 = 377 0мх8,8х104 Ом'1 м'1 =2,3х106 м"' пж{т)2 3,6x4

Таким образом, ИК-излучение поглощается на глубине порядка 0,4 мкм.

• модель ничего не говорит о микроскопической природе процесса поглощения на свободных носителях (взаимодействие с примесями, акустическими фононами и т. д.).

Для решения этих проблем необходимо обратиться к квантово-механической трактовке. Одновременно мы должны осознавать, что квантово-механический ана­лиз будет сопряжен с рядом трудностей, которые надо преодолеть прежде, чем он сможет предложить удовлетворительное описание поглощения свободным элект­ронным газом. Рисунок 7. В.2 один из таких аспектов рассмотрения.

Сг

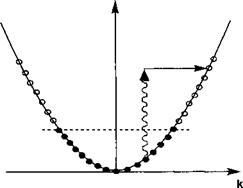Рис. 7.В.2. Поглощение фотона в од­ной зоне возможно только в случае участия механизма рассеяния, который может обеспечить необходимое сохра­нение импульса между начальным и ко­нечным состояниями.

Как мы видели в начале главы, матричный элемент, описывающий связь между зонным электроном и электромагнитной волной является ненулевым только для практически вертикальных переходов, при которых сохраняется волновой вектор к. Поскольку квазисвободные электроны распределены по параболической зоне про­водимости полупроводника, то доступных состояний «над» этой зоной, которые могли бы принять возбужденный электрон не имеется. Другими словами, мы не можем одновременно удовлетворить условия сохранения импульса (к = к') и энер­гии (И2к2 / 2тс{{ + Иу= к2к2/2тс{{). Таким образом, нам необходимо другое взаимо­действие для обеспечения дополнительного импульса с тем, чтобы возвратить воз­бужденный электрон обратно в зону проводимости.

Для этого мы располагаем всеми механизмами, описанными в главе 6 (примеси, оптические фононы и т. д.) В качестве примера рассмотрим взаимодействие с оптичес­кими фононами, описываемое гамильтонианом взаимодействия 1/2(Н + к. с.). Поскольку этот переход требует участия двух одновременных возбуждений, мы дол­жны использовать теорию возмущений второго порядка, к которой мы прикосну­лись в дополнении З. Б. Уравнение (З. Б.26) дало нам скорость перехода в секунду между начальным |/) и конечным |/) состояниями:

Эта формула использовалась в контексте двухфотонного поглощения. Здесь же мы имеем Н

Два другие члена в сумме соответствуют двухфотонному поглощению (в виде членов типа (/|#ор|я) (я|#ор|/)) и двухфононного рассеяния (в виде членов типа (/|#рЬ|л) (я|#рЬ|/)). Естественно, такие переходы не обеспечивают одновременное сохранение энергии и импульса. В интегральном виде закон сохранения энер­гии в процессе различных переходов второго порядка может быть выражен в виде:

) = S(Ef - Е, - hcoop ± ha>ph)

В зависимости от того участвует ли в процессе поглощение или излучение фононов. Хотя принцип, лежащий в основе этих вычислений, понятен, на практике сумми­рование по промежуточным состояниям достаточно утомительно. Этот расчет мо­жет быть изучен по книге Ридли (1988).

С учетом сложности этих квантовых моделей часто используется феноменоло­гические формулы, полученные из эксперимента. Поглощение на свободных носи­телях может быть описано соотношением:

N (см ~3) Я(мкм )

Ю17 JL 9

Где Ка есть параметр, зависящий от материала и приведенный в таблице 7.В.1 для различных полупроводников.

(7.В.16)

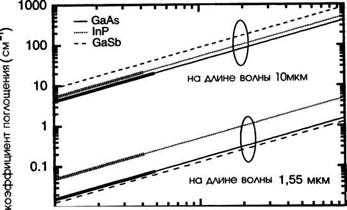
На рисунке 7.В. З представлены коэффициенты поглощения ряда полупровод­никовых материалов, важных для оптоэлектронных применений (ваАБ, 1пР и СаБЬ), в функции концентрации свободных электронов и для двух практически важных длин волн: 1,55 мкм (для телекоммуникационных целей) и 10 мкм (для оптических оборонных применений).

Мы видим, что паразитное поглощение может быть значительным и его следует учитывать при расчетах порогов лазерной генерации.

Поглощение на свободных носителях приводит к изменению Ае в полупровод­никовых материалах. Для определения амплитуды этого эффекта нам необходимо только ввести выражение (7.В. 10) в дисперсионное соотношение (7.В.4) и просум­мировать действительные части к2. В этом случае мы находим:

..2

(7.В.17)

Где сор есть плазменная частота электронного газа, определяемая соотношением:

(7.В.18) Плазменная частота

Это изменение показателя преломления используется в электро-оптических моду­ляторах. Как показано на рис. 7.В.4, электромагнитная волна каналируется облас-

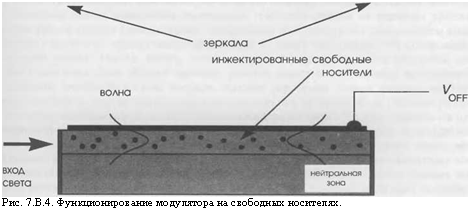Тью пространственного заряда (смотрите главу 10), расположенной между двумя зеркалами, находящимся с двух сторон волновода.

Этот волновод длиной Ь ведет себя как резонатор Фабри—Перо с пропуска­нием, определяемым (9.Г.21). Интуитивно понятно, что волновод пропускает из­лучение с волновым вектором £, когда кЬ = тж (включенное состояние) и блоки­рует излучение, когда кЬ = (2т + )ж/2 (выключенное состояние). Под влиянием приложенного извне напряжения электроны инжектируются в область простран-

Ственного заряда и модулируют е в соответствии с (7.В. 17), что переводит волновод из включенного в выключенное состояние. Напряжение, необходимое для переклю­чения состояния модулятора, дается соотношением:

(7.В.19)

Это соотношение с учетом дисперсионного соотношения к = 0)£/2/с = 2/шор/А0, где Л0 есть длина волны в вакууме, может быть записано в виде:

Д£=-^-у (7.В.20)

Пример--------------------------------------------------------------------------------------------------------------

Рассмотрим волновод на основе 1пР (пор = 3,5, те{{ = 0,077т0). Мы хотим определить длину волновода для его переключения на длине волны Л0 = 1,55 мкм при инжек - ции в область пространственного заряда 1017 носителей/см-3. Плазменная частота сор электронного газа дается (7.В. 18) и составляет:

^■^,86>|0-|-Фм-|х0,077х0.9*10-»кгМ, Х'<)''' - М*'»" <7' »•’■>

На длине волны 1,55 мкм частота составляет 1,2 х 1015 с-1, что приводит к изме­нению е величиной Д£ = — 3 х 10_3. В этом случае необходимая длина прибора в соответствии с (7.В.20) составляет:

Ь = 3,5 х 1,55 х 10~3 мм/(2 х 3 х 10_3) = 0,9 мм