Оптоэлектроника

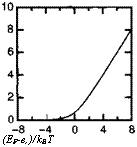
Плотность состояний и статистика системы с квантовой ямой

В каждой подзоне электронные состояния содержат компоненту в виде плоской волны в направлении, параллельном границам раздела. Как это уже неоднократно делалось для трехмерного континуума (смотрите Дополнение 1.А, раздел 5.3, ...) и сейчас включим двумерную квантовую яму в плоскость за счет использования мак­роскопической прямоугольной области с площадью Л = ЬхЬу. Граничные условия на краях этой прямоугольной области (или иначе — «виртуального ящика») вводят квазиквантование допустимых значений импульса й К. В соответствии с цикличны­ми граничными условиями Борна—фон Кармана (смотрите раздел 5.2):

¥{х, У,1)=чг{х+ 1х, у,г) ¥{х, у,г)= у/(х, у+ Ьу^)

Применительно к волновым функциям в (8.26) это условие означает:

К = (кх, к,)-

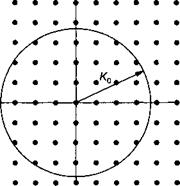Где пх и п являются целыми числами. Если мы будем представлять допустимые значения К в виде точек на плоскости (рис. 8.7), то в этом случае каждое состояние будет занимать площадь (2ж)2/Ьх Ьу, при этом плотность состояний в этом двумер­ном пространстве К будет постоянной, т. е. /)(К) = gA/(2л)2.

Рис. 8.7. Квазиквантованные значения для К = (2япуЬх, 2тту/Ьу) представляются точка­ми в плоскости обратного пространства. Со­стояния, обладающие энергией менее Е0, зак­лючены в круг радиуса К0 (уравнение (8.39)). к

''х

В последнем выражении было учтено вырождение по спину = 2, так как каждое состояние К допускает два решения с противоположными спинами.

Нам часто приходится вычислять суммы функций /, зависящих только от энер­гии состояний:

£/[£(К)]= |^гс12К /[£(К)]= | ДЕ)Оп(Е)йЕ (8.38)

Здесь Оп(Е) представляет собой плотность состояний в я-ной подзоне. В предполо­жении параболичного характера дисперсии, подобного уравнению (8.35), число со­стояний АТп(Е0) с энергией меньше Е0 будет равно числу состояний с волновым вектором К, лежащим внутри окружности радиуса К0 = (2т„(Е0 — £п)/Ь2У/2' как это и показано на рис. 8.7, т. е. при Е0 > е

М„(Е0)=1?Ц-хК02 = (8 39)

2я) яЬ

Таким образом, плотность состояний в подзоне является постоянной:

(840)

При Е< еп не имеется допустимых состояний и Оп(Е) = 0, что отражается функцией Хэвисайда в.

В этом случае плотность состояний в системе дается суммой плотности состоя­ний для каждой подзоны.

В(Е)= £ /)„(£)= *Ш^^е{Е-еп) (8.41а)

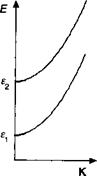
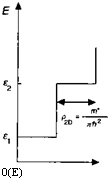Рис. 8.8. Подзоны и плотность состояний для двумерной структуры.

Эта функция имеет ступенчатую форму (рис. 8.8), при этом высота ступеньки явля­ется константой материала. В то же время положение ступенек зависит от конкрет­ной величины ет и, таким образом, от потенциала, ограничивающего электроны в дискретных подзонах. Часто используется двумерная плотность состояний р1Ь в расчете на одну подзону и единицу площади (эВ-1 см-2), которая определяется соот­ношением:

Dn(E).

ПЬ

Двумерная плотность состояний

При термодинамическом равновесии вероятность того, что электрон занимает состояние с энергией ЕпК, по-прежнему определяется статистикой Ферми:

1

Жк) =

1 + exp [(£„к - Ef )/ kBT ]

Где Ef есть энергия Ферми. Поверхностная концентрация пп электронов в подзоне п, таким образом, составляет:

(8.43)

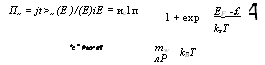Критическая концентрация

Где пс есть критическая концентрация носителей в подзоне. Полная поверхностная концентрация носителей в системе в этом случае определяется соотношением:

(8.44)

Уравнения (8.43)—(8.44) определяют п$ в функции Ер и Т. Они позволяют однозначно определить уровень Ферми, если известна величина п$.

Если энергетический зазор между самыми нижними уровнями превышает тепловую энергию (т. е. е2 — ех » квТ), а концентрация п5 не слишком велика, то заселена будет лишь одна подзона и мы можем выразить пхи ЕР в виде:

F r-1

EF-e 1 kj

Ef = ej + kBT In

Уравнение (8.45) показывает, что в двумерном электронном газе имеет место переход от вырожденного к невырожденному режимам. В том случае, когда п$ » пс, мы получаем условия вырожденного электронного газа, для которого:

Ns — P2d(Ef е) Ef = е, +

PlD

В случае невырожденного режима я « пс, при этом:

£*, - EF

П5 = пс ехр --к~~

(8.47)

Я.

Ef =е, - к„Т п

Я,

V /

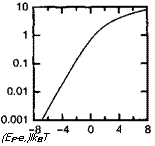
На рис. 8.9 в линейном и логарифмическом масштабах представлены зависимости п (Е' ).

I

Рис. 8.9. Плотность состояний в подзоне в функции положения уровня Ферми ЕрВ линейном (а) и логарифмическом (б) масштабах.

Пример--------------------------------------------------------------------------------------------------------------

Рассчитаем плотность состояний и критическую концентрацию для квантовой ямы ваАБ.

Эффективная масса тс в СзАб составляет 0,067т0, что приводит к плотности рю:

Р2В = 1,6x10^ Кл - 0’0-ухО,9хЮ:30 кг = з зв-, см-2

3, 14x(l,05xl0'34 Дж cj

В этом случае критическая концентрация составляет пс = рт х 25,9 мэВ или 7,2 х 1011 см-2.

Таким образом, квантовая яма, легированная до уровня 1012 см-2, является вырожден­ной. Разность между положением уровня Ферми и энергией ограничения в этом случае составляет:

Ер-е{ = 1012 см 2 /(2,78х1013 эВ-1 см'2)=36мэВ