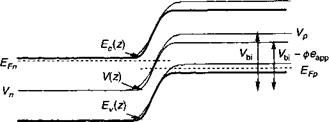
Переход с барьером Шотки
При контактировании металла и полупроводника более не существует барьера между каждым из этих материалов и вакуумом, при этом электрон с энергией, превышающей высоту барьера Ес(0) может перемещаться между металлом и полупроводником. При термодинамическом равновесии концентрация электронов у поверхности, обусловленная полупроводником, описывается классическим выражением:
|
= ехр |
|
Ш - Е, КвТ |
|
|
|
|
|
|
При большой высоте барьера фв по сравнению с квТэта концентрация, естественно, очень мала по сравнению с концентрацией носителей заряда внутри полупроводника:
|
|
|
|
Здесь еУЛ = Ес(0) - £(«>).
Среди поверхностных электронов с концентрацией п (0) половина имеет компоненту скорости, направленную к металлу, а другая половина имеет компоненту скорости, направленную к полупроводнику. Средняя скорость электронов, направленных к металлу, составляет:
|
Ь |
|
Ехр - |
|
2квТ |
|
|
|
|
|
|
Это соответствует плотности тока:
2
|
КвТ |
![]() (10.14)
(10.14)
До тех пор, пока система находится в равновесии, этот ток полностью компенсируется током, протекающим в противоположном направлении от металла к полупроводнику:
J.^m = - У,.,, (Ю.15)
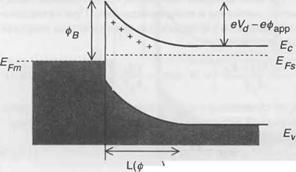
Если мы приложим напряжение фарр, то получим (смотрите рис. 10.3):
ЕР, т = Е^-еф^ (10.16)
Здесь предполагалось, что уровни Ферми располагаются вдали от перехода. В металле проводимость столь велика, что никакое падение напряжения невозможно и, таким образом, Ес(0) остается на уровне ЕР т + ефв. Таким образом, приложенный потенциал ограничен областью полупроводника, которая должна так модифицировать область обеднения, чтобы падение потенциала стало равным Ес(0) — £(°°) = еУ6 — ефйрр.
Примечание: такая модуляция длины обеднения Ь с приложенным напряжением приводит к емкости С, определяемой приращением заряда из-за изменения приложенного напряжения 6фа :
|
А <*Фа, |
|
|
||
|
|||
|
|||
|
Металл |
![]()
|
Полупроводник |
![]()
|
Арр' |
![]()
 Эта емкость есть функция приложенного напряжения — свойство широко используемым в ВЧ-применениях. Таким образом, барьер Шотки действует как варактор, характеризуемый переменным реактивным сопротивлением. Если приложенный сигнал является суммой сигнала с малой амплитудой с частотой со$ и амплитудой У$, а локальный генератор обладает частотой со0 = о)5 — Асо и амплитудой У0 » К, реактивный ток будет обладать компонентой на разностной частоте А со. Этот ток может быть записан в виде (б =
Эта емкость есть функция приложенного напряжения — свойство широко используемым в ВЧ-применениях. Таким образом, барьер Шотки действует как варактор, характеризуемый переменным реактивным сопротивлением. Если приложенный сигнал является суммой сигнала с малой амплитудой с частотой со$ и амплитудой У$, а локальный генератор обладает частотой со0 = о)5 — Асо и амплитудой У0 » К, реактивный ток будет обладать компонентой на разностной частоте А со. Этот ток может быть записан в виде (б =
Рис. 10.3. Переход Шотки при приложении прямого напряжения 0арр. Область обеднения сужается, при этом концентрация электронов со стороны полупроводника возрастает, приводя к потоку электронов из полупроводника в металл.
|
Ае <10арр __ <•/ (10.18) = - с (о Этот ток содержит компоненту с частотой Асо: Й1 (1 ^арр (1/ 2^2 В общем случае, в токе диода содержатся все частоты со0 ± со0, *у0 ± ± *У0.Таким Образом, варактор преобразует высокочастотный сигнал с частотой со5 в сигнал с промежуточной или низкой частотой сох — со0. Следовательно, такой прибор является полезным при гетеродинном детектировании. Подобно другим нелинейным приборам варактор также реализует функции удвоения частоты и выпрямления с частотой со5 — со0. Позже мы возвратимся к этому при рассмотрений концепций нелинейной оптики. |
|
У0 СР5Ц/)+ У$ СОБ^/) |
|
(У0а>0 5тЦ/)+ У^ (а/)) |
|
1 + |
|
2 к, |
|
|
"(о) |
![]()
|
*Фв К»Т |
![]() (10.20)
(10.20)
В то же время со стороны полупроводника происходит изменение барьера. И именно такая асимметричная реакция полупроводника и металла приводит к выпрямительным характеристикам диода. Для упрощения расчетов предположим, что диффузионный перенос (и следовательно подвижность) очень велик в полупроводнике. Кроме того, мы предположим, что перенос электронов приведет лишь к незначительному возмущению равновесного состояния полупроводника. В этом случае концентрация носителей с полупроводниковой стороны перехода составит:
|
ЕЛо)-е,„ К. Т |
|
ЕФв - еК К. Т |
|
= Ме ехр |
|
|
|
|
|
Чер ,)= I |
|
1 |
|
Js-,m =е%1-^—Лсех р В этом случае результирующий ток через структуру составит: ЕФлрр |
|
При этом плотность тока, направленного к металлу, будет равна: 'еф ' ’ аРР |
|
К„Т |
|
К„Т |
|
Ехр |
|
Ехр |
 |
|
|
|
|
|
|
Ж 2 ттс |
![]() Вольт-амперная характеристика диода Шотки При этом плотность тока насыщения у дается выражением:
Вольт-амперная характеристика диода Шотки При этом плотность тока насыщения у дается выражением:
|
( , л еФв |
Аек1птс ~ 2 =------- —-Т ехр |
/ |
1 1 ^ |
= А*Т2 ехр |
Ефв |
|
КвТ V в ) |
К |
Ч |
КвТ J |
КвТ V в У |
|
Ехр |
|
(10.24) |
Постоянная А* называется константой Ричардсона. В предположении эффективной массы тс = т0 ее величина составляет А = 120 А см-2 К-2. Типичный график в соответствии с (10.24) показан на рис. 10.4.
|
0,2 0,025 |
|
= 0,15 мка |
|
/ = /« |
|
-1 |
|
Ехр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
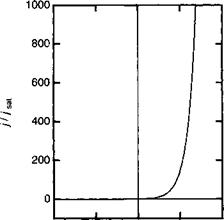
При 0арр = 0,4 В его величина равна / = 0,44 мА. Сопротивление диода при фар = О равно:
|
Vі |
|
Л |
|
К„Т |
|
0,025 |
|
*оА = |
|
0,5x10' |
|
/Ф, рр-0 |
|
Ом см2 =50 кОм см2 |
Для детального учета характеристик реальных диодов Шотки к идеальной модели следует добавить ряд коррекций. Во-первых, электронный перенос в области обеднения может быть ограничен способностью полупроводника переносить электроны, когда коэффициент их диффузии мал. Другими словами, при прямом смещении их концентрация п(0) будет меньше равновесного значения для полупроводника (уравнение (10.21), при этом величина инжектированого в металл потока будет уменьшена. Это должно приводить к модификации коэффициента перед экспонентой уза{ в /— К-характеристиках, в то время как зависимость от ф^ остается неизменной.
Более того, высота барьера может быть уменьшена из-за заряда изображения. Электрон, покидающий металл, поляризует электронный газ в металле. Результирующее при этом сродство электрона к металлу, известное из электростатики, может быть представлено в виде притяжения этого электрона к одиночному виртуальному заряду изображения Кт(г) = —&/(4^(2^)), где г есть расстояние между электроном и поверхностью металла. Это приводит к добавлению члена —ер1 к потенциалу области обеднения, что приводит к уменьшению максимума этого потенциала по отношению к фв Утах = фв — (еР/А£)1/2. Таким образом, полная высота барьера уменьшается, что приводит к увеличению ую1 и проявлению зависимости плотности тока от напряженности поля Р (от приложенного напряжения). К тому же, если напряженность Р очень велика, что имеет место в случае сильно легированного полупроводника даже при малых приложенных напряжениях, электроны могут пересекать переход за счет туннелирования, при этом Вольт-амперные характеристики становятся линейными. В этом случае переход называется омическим контактом.
И наконец, источником дополнительного тока может быть и ряд паразитных процессов (генерация электронно-дырочных пар в области пространственного заряда, токи утечки по периметру контакта и т. д.). Эти процессы сильно зависят от особенностей конкретного процесса изготовления контактов. На практике эти па-
Разитные эффекты учитываются введением коэффициента идеальности п, который всегда >1, что является проявлением природного закона Мэрфи, и который определяется из измерения характеристик контакта:
|
-1 |
|
Ехр |
|
ПккТ |
|
Жрр)= л. Диод Шотки идеален, когда п= 1. |
|
|
10.1. р-п-Переход
Р—«-переход образуется легированным полупроводником р-типа с одной стороны перехода и легированным полупроводником «-типа с другой стороны перехода. /— К-харак - теристика для тока пересекающего такой переход в функции приложенного напряжения, который проявляет выпрямляющий характер подобно тому, как это было в случае диода Шотки. В то же время процесс, ответственный за это, имеет другой характер.
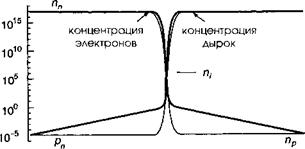
Начнем с рассмотрения резкого р-п-перехода в условиях термодинамического равновесия (т. е. перехода, в котором тип легирования изменяется в пределах очень малого расстояния по сравнению с протяженностью области пространственного заряда — смотрите рисунок 10.5). При I > 0 полупроводник имеетр-тип проводимости с постоянной концентрацией акцепторов Л^. Вдали от перехода уровень Ферми располагается, вблизи валентной зоны, и концентрация дырок в валентной зоне есть рр = ЫА, где
Индекс «р» обозначает /7-сторону перехода. К тому же, вследствие теплового равновесия мы имеем пр = п} и концентрация электронов составляет п = я.2 /ИА, при этом они являются неосновными носителями при условии, что п « Л^. (5 п-стороны перехода (при г < 0) полупроводник легирован донорами до постоянного уровня Л^. Таким образом, вдали от перехода уровень Ферми располагается вблизи зоны проводимости, при этом концентрации основных носителей-электронов и неосновных носителей-дырок составляют соответственно п = Ип и р = п?/Мп « п.
П й Г п I / о п
|
УУ,.7УС |
![]()
|
(10.26) |
![]()
|
Кы = (£, - £,.)„ - (£, - £Д = £, - квТ 1п |
![]()
|
Здесь мы использовали (5.52) и (5.54) для расчета положения уровней Ферми в функции уровней легирования. Физическая причина возникновения потенциального барьера заключается в следующем. Если мы представим себе, что мы приводим в контакт п - и /7-области полупроводника, то основные носители с обеих сторон перехода будут диффундировать в другую область (т. е. в область, где они присутствуют в качестве неосновных носителей), как это и следовало ожидать из закона Фика. В отсутствие какого - либо противодействующего механизма как электроны, так и дырки продолжали бы диффундировать до тех пор, пока их концентрации не стали бы постоянными по |
 Вдоль перехода концентрация дырок не может изменяться скачком от рп до рр. Следовательно, существует область около г = 0, где р(1) < рр = Л^. Аналогичным образом, в случае электронов мы также имеем область, где п(г) < пп = Ы0. В условиях равновесия всегда выполняется я(г)/?(г) = я 2, но сумма концентраций подвижного заряда будет намного меньше концентраций фиксированных ионизированных атомов примеси. Таким образом, область обеднения характеризуется плотностью заряда — еМА с р-стороны перехода и положительным зарядом еЫ0 с «-стороны перехода. Дипольный слой ответственен за формирование электростатического потенциала по обе стороны перехода. В условиях равновесия этот потенциал обеспечивает выравнивание уровней Ферми электронов и дырок. Он всегда существует в условиях равновесия и поэтому называется встроенным потенциалом, при этом его величина определяется выражением:
Вдоль перехода концентрация дырок не может изменяться скачком от рп до рр. Следовательно, существует область около г = 0, где р(1) < рр = Л^. Аналогичным образом, в случае электронов мы также имеем область, где п(г) < пп = Ы0. В условиях равновесия всегда выполняется я(г)/?(г) = я 2, но сумма концентраций подвижного заряда будет намного меньше концентраций фиксированных ионизированных атомов примеси. Таким образом, область обеднения характеризуется плотностью заряда — еМА с р-стороны перехода и положительным зарядом еЫ0 с «-стороны перехода. Дипольный слой ответственен за формирование электростатического потенциала по обе стороны перехода. В условиях равновесия этот потенциал обеспечивает выравнивание уровней Ферми электронов и дырок. Он всегда существует в условиях равновесия и поэтому называется встроенным потенциалом, при этом его величина определяется выражением:
всей структуре. Однако, заряженные атомы легирующей примеси противодействуют этому механизму. По мере того, как все большее число носителей переходит на другую сторону перехода, амплитуда пространственного заряда, сформированного остаточными ионизированными атомами примеси, увеличивается, что создает энергетический барьер, который препятствует и, в конце концов, прекращает дальнейшую диффузию носителей. Таким образом, мы видим, что диффузия носителей будет играть доминирующую роль в работе р-п-диода. Именно по этой причине встроенное поле иногда называют диффузионным потенциалом. Мимоходом еще раз отметим эффективность концепции уровня Ферми. Этот параметр определяет электронное сродство в каждом из материалов и учитывает химические потенциалы, электростатические потенциалы и т. д. Результирующим распределением будет то, которое обеспечивает постоянное положение уровня Ферми по всей структуре.
Теперь мы уже можем идти вперед и рассчитать электростатический потенциал ф(1) или, что проще, рассчитать потенциальную энергию электронов V(г) = Используем аппроксимацию области обеднения, поскольку она существенно упро-
Щает расчеты — т. е. мы пренебрежем влиянием носителей на распределение потенциала в области пространственного заряда.
Таким образом, в интервале — с1 < I < 0, уравнение Пуассона имеет вид:
SHAPE \* MERGEFORMAT ![]()
|
(10.27) (10.28) (10.29) (10.30) |
![]() ^-е-ы ае £ 0
^-е-ы ае £ 0
При этом его решение представляет собой:
Ук^Г' + ^-НоЬ + ё'У
2е
В /^-области при 0 < I < с! уравнение Пуассона имеет вид:
Скг е А
При этом соответствующее решение определяется выражением:
>2
Р ^ г " ' Л V- ~ Р >
У перехода, расположенного при г = 0,физическая непрерывность потенциала и его первой производной, т. е. электрического поля, приводит к следующим условиям:
|
(10.31) |
![]() V + — N (Iі - V - — N Л1
V + — N (Iі - V - — N Л1
• 2е р 2е Ар
Носі, = МАСІР
При этом, поскольку V — К = Уы, решения приобретают вид:
(10.32)
Е2 Мв + {М0/МА) 2е К, 1
</2 =
Р
В2 ЫА 1 + (^/УУ0)
Присутствие потенциала смещает зоны в полупроводнике, поскольку энергия электронов увеличивается вдоль структуры в каждой точке на величину ~еф(?) = К(г):
Е'к)= Ес(- Ю+ У^)- у„ (10-33)
Е,(г)= Ес{7.)~ Ее = Е, К)+ К(г)- Ур
|
(10.34) |
![]() Исходя из этой конфигурации энергетических зон для Ес(1) и £(г), мы можем рассчитать концентрации электронов и дырок:
Исходя из этой конфигурации энергетических зон для Ес(1) и £(г), мы можем рассчитать концентрации электронов и дырок:
|
П(г)= ехр |
Ес{г)- Ег [ квТ |
= N 0 ехр |
Г Ук)-УА КвТ |
|
Р{г)= Аг„ ехр |
Ег-еЛії КвТ |
= ЫА ехр |
У,-уЩ Квт |
В частности, мы находим, что:
|
П(с1р)= Л^ехр Р(-<0 = Ка ехр |
|
= Пп |
|
К. Т Уы Квт |
|
Рп |
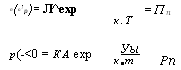 |
|
|
|
|
|
Таким образом, для условий термодинамического равновесия мы определили: вид потенциала У(г), зонную диаграмму для £(г) и ЕДг), ширину областей пространственного заряда и концентрации носителей в каждой точке.
Пример---------------------------------------------------------------------------------------------------------------------------------------------------
Рассмотрим р—л-переход на основе СаА$, каждая область которого легирована до уровня = 1017 см“3. Отыщем диффузионный потенциал Уъ. и электрическое поле в переходе при I= 0. Из уравнения (10.26) мы имеем:
4,7х 1017 х 7,Ох 1018
|
= 1,27 эВ |
![]() Уы = 1,42 эВ - 0,025 эВ 1п
Уы = 1,42 эВ - 0,025 эВ 1п
)
При этом (1п = <1 = 92 нм. Таким образом, слой обеднения очень тонок. Максимальная напряженность поля имеет место при I = 0 и она равна:
„/Лч 1(1 У е кт, 1,6х 10"19 1Л23 1Л_8 В 1<зп п
Л0)=—— = - Дг и = ■ *- ■-—гг-ггЮ" х9,2х 10 8 —= 139 кВ см к ' е е 12х8,84х 10 м
Ясно, что в условиях равновесия через структуру не будет протекать ток. Вне области обеднения не существует ни электрическое поле, ни градиент концентрации носителей. С другой стороны, в области обеднения имеется сильное электрическое поле, а также значительный градиент концентрации носителей. Постоянное положение уровня Ферми по всей структуре гарантирует, что все компоненты тока будут взаимно компенсироваться, если диффузионный профиль будет таким, как он описывается (10.34). Перед тем, как перейти к рассмотрению приложения напряжения к структуре, полезно представлять себе порядок различных параметрических длин, которые характеризуют переход. Область, определяемая z< 0, представляет собой колоссальный резервуар свободных электронов, сдерживаемых потенциалом области обеднения. Лишь незначительная концентрация неосновных электронов может просочиться в /7-область перехода. Подобным же образом область г > 0 образует резервуар для дырок, сдерживаемый потенциалом области обеднения. Наконец, в нейтральных областях увеличенная концентрация основных носителей обеспечивав высокий уровень проводимости, что приводит к нулевому электрическому полю в этой области. Таким образом, потенциал остается постоянным по обе стороны области обеднения даже в условиях не очень сильных токов.
Приложение слабого прямого смещения фарр (т. е. такого, которое уменьшает высоту барьера) приводит к энергетическому зазору между уровнями Ферми по обе стороны области обеднения (смотрите рис. 10.6):
ЕР%, = ЕР"-фш рр (10.36)
В нейтральных областях потенциал остается постоянным, при этом единственной областью, в которой возможно изменение падения напряжения, является сужающийся обедненный слой. Этот эффект может быть учтен заменой в (10.31) К на У — еф, что дает:
Р "арр5
|
(10.37) |
![]() 4,(0)^ = <(о^1 - ^
4,(0)^ = <(о^1 - ^
|
1 - |
![]()
|
2 Уы |
![]() Л„ + <1р = Ь„(0) + (0)]
Л„ + <1р = Ь„(0) + (0)]
В резервуаре электронов потенциал при <1р понижается до уровня V — ефт. Поскольку область обеднения узка, мы можем предположить, что электронный резервуар будет в равновесии вплоть до с! р. Таким образом, концентрация электронов в соответствии с (10.34) и (10.35) есть:
|
|
|
А О Т. О |
(а)
|
=Г 0 А Н- 1 0 =г 1 О |
|
(б) |
|
|
|
|
УЮ-К |
|
= пп ехр |
|
К, Т |
|
ЕФ: |
|
Арр |
|
КвТ Условие Шокли |
|
(10.38) |
|
V,: |
|
КвТ |
 |
|
Мы напоминаем, что п = п?/есть равновесная концентрация неосновных носителей. Уравнение (10.38) имеет фундаментальное значение с точки зрения описания р—я-перехода и оно называется условием Шокли. При I = ^ имеется избыток электронов по сравнению с равновесным значением п. Этот избыток электронов должен быть удален через ^-контакт (при г — IV на рис. 10.5) или за счет рекомбинации с дырками в области (1 < г < IV. В о(юих случаях возникает ток между переходом и р-контактом. Важно помнить, что до тех пор, пока ефарр < Уь. электроны останутся неосновными носителями с концентрацией на несколько порядков меньшей по сравнению с концентрацией дырок и, как следствие, нейтральность заряда в р-области останется сравнительно ненарушенной из-за инжекции электронов. И как результат, отсутствует поле, способное удалить электроны из этой области (т. е. в обратном направлении!). Таким образом, единственной возможностью переноса является диффузия. В этом случае уравнение переноса электронов (смотрите (6.60)) имеет достаточно простой вид:
|
«(г)- пр |
![]()
|
(10.39) |
![]() Эл _ Э Эл Э7 Э? ”ЭГ
Эл _ Э Эл Э7 Э? ”ЭГ
В стационарном состоянии имеет место уравнение:
|
0 |
![]()
|
(10.40) |
![]() „ ъ п л(г)-и,
„ ъ п л(г)-и,
П 2
Здесь йп есть коэффициент диффузии для электронов в р-области, а г есть их время жизни до рекомбинации с дырками. Введем диффузионную длину:
|
В том, что касается второго ограничивающего условия, мы будем моделировать контакт при I = №р временем жизни, которое настолько мало, что электроны и дырки находятся в термодинамическом равновесии с уровнем Ферми-контакта. Так, что: |
|
Дя(^,)-0 |
|
(10.436) |
|
(W. |
|
Sinh |
|
Ди(^)=и, |
|
-1 |
|
Ехр |
|
KJ |
|
Э2Лп An{z) _ Эг2 L] |
|
(10.42) Условие Шокли (уравнение (10.38)) позволяет рассчитать Ап на краю области обеднения: |
|
|
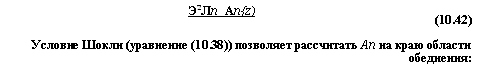 |
|
|
|
 |
|
|
|
|
An(z)= An(dp) |
|
Pt / Sinh |
|
W - d P p |
|
|
|
При этом имеют место два предельных случая: Z-d Л |
|
An(z)= An(dp )ехр |
|
(10.45) |
|
Z~d, К ~dP |
|
An(z)= А «(</,) |
|
1- |
|
Первый предельный случай соответствует ситуации, когда ни один из инжектированных электронов не может достичь контакта, поскольку они уже проре- комбинировали с дырками. В этом случае полный ток должен сохраняться, и по мере того, как мы удаляемся от перехода (т. е. I увеличивается в направлении от й к IV) электронный поток постепенно заменяется дырочным с тем, чтобы поддержать процессы рекомбинации. Во втором предельном случае диффузионная длина достаточно велика настолько, что все электроны, инжектированные при I = с1р достигают ¥р, не рекомбинируя с дырками. Во обоих случаях полный ток, генерируемый инжекцией электронов, является диффузионным током при z= с1р (положительным, если он направлен от /7-области к я-области), т. е.: |
|
W „ - d. |
|
Cosh |
|
W - d P p |
|
Sinh |
|
- 1 |
|
Ехр |
|
= Jn |
|
KRT |
|
Ехр |
|
KRT |
|
J = Jn(dp) = — Dz |
|
= — L. |
|
Z=dp |
|
|
 |
|
|
|
|
|
|
|
ЈAl _ьL К * А wn NД |
|
-1 > л = л* + л* (10.53) Вольт-амперная характеристика р—л-диода |
|
-ехр |
|
N, |
|
КаТ |
|
Аp(z)= Аp(-d„)- |
|
-d + W |
|
Sinh |
|
Л |
|
,)=л |
|
Ехр |
|
КвТ в у |
|
При этом предел диффузионного тока для дырок составляет: |
|
E_D^n[_ L, N0’ _ eDP nf W-d„ ~ W„ Nr |
|
PneD. |
|
Ln « Wu |
|
PneDp |
|
- d. + |
|
Coth |
|
J DS |
|
P eD Г n p |
|
« Ln |
|
Таким образом, ток, обусловленный инжекцией дырок в область я-типа составляет: |
|
^арр К„Т |
|
У, = jP{~d„)= , |
|
(10.51) |
|
-1 |
|
Ехр |
|
При этом уравнение диффузии для неосновных дырок в я-области (— ¥п < г < ~йп) в этом случае имеет вид: (12Ар А |
|
(10.49) |
|
Dz |
|
Здесь: Ь2 = Ортр есть квадрат диффузионной длины дырок в я-области. Решение последнего уравнения с граничными условиями при г ~ ~ №п = ~с1п аналогично (10.44) и приводит к следующему уравнению для концентрации избыточных дырок: |
|
Р(-^„)= р„ ехр |
|
КйТ |
|
||
|
||
|
||
|
||
|
||
|
||
|
||
 |
||
|
||
|
||
 |
||
 |
||
|
||
|
||
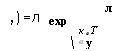 |
|
|
Мы обсудили случай, когда ефарр > 0, при котором инжектируются неосновные носители. При ефйрр < 0 в условиях обратного смещения уравнения остаются теми же самыми за исключением того, что вместо избытка неосновных носителей в данном случае имеет место их дефицит, способствующий генерации электроннодырочных пар в нейтральных областях. Вольт-амперные характеристики по-прежнему описываются уравнением (10.53), но при этом ефйрр < 0.
Пример--------------------------------------------------------------------------------------------------------------
Для перехода на основе СэАб мы имеем = 1017 см-3. Если подвижность элек
Тронов в /7-области составляет /лп = 5000 см2 В-1 с-1 при аналогичном параметре для дырок в я-области // = 800 см2 В-1 с“1, то мы находим с использованием соотношения Эйнштейна £>п = у]свТ/е = 5000 х 0,025 см2 с-1 = 125 см2 с-1 и Бр = 20 см2 с-1. При времени жизни носителей г = т = 1 не диффузионные длины составляют Ьп = 3,5 мкм и Ьр = 1,4 мкм, что явно намного больше области обеднения. Собственная концентрация носителей определяется (5.49) и составляет п. = 1,8 х 106 см“3. Таким образом, диод с большой толщиной обладает следующими пределами диффузионного тока:
|
-18 |
![]() J _ я,2еР„ _ (1,8x1012)2Х 1,6x10-19 X 125x10-4 А _1о;;|0
J _ я,2еР„ _ (1,8x1012)2Х 1,6x10-19 X 125x10-4 А _1о;;|0
NaL„ 10 23 х3,5x10-6 м
N? eDp _ (l,8 х 1012 )2 х 1,6 х 10~19 х 20 х 10~4 _А_ _ q 7 х jq-is А NdLp 1023 х 1,4 х 10~6 м2 ’ см:
Таким образом плотность обратного тока составляет= 2,5 х 10 18 А см 2, а сопротивление диода при фа =0 есть:
|
Э/ |
|
R0A = |
|
Ъфч |
|
= = .°’°25 18 Ом см2 = 1016 Ом см2 А» ^ 2’5х10“ |
Приведенные значения предельных токов очень малы. В действительности же при рассматриваемых условиях в измеряемых токах доминируют токи утечки, связанные с дефектами (смотрите дополнение 10 Б).
Выражение для Вольт-амперной характеристики (уравнение (10.53)) заслуживает нескольких завершающих комментариев:
1. Зависимость от фарр имеет тот же самый характер, что и в случае диодов Шотки. В то же время различие в коэффициентах отражает тот факт, что характеристика определяется одновременным проявлением ряда механизмов. Диод Шотки является униполярным прибором, в котором протекание тока определяется переносом основных носителей. В то же время р-п-диод является биполярным прибором, в котором перенос носителей контролируется неосновными носителями в каждой области.
2. Р-п-диод является лучшим выпрямительным прибором, когда диффузионные токи минимальны. Широкозонные полупроводники (с малой величиной л2) с высоким уровнем легирования и большими временами жизни наиболее благоприятны для решения проблемы, связанной с диффузионными токами.
3. При использовании сильно асимметричной схемы легирования (например, ЫА
Весь ток является результатом инжекции электронов В /7-область в то время, как инжекция дырок минимизирована. Аналогичный эффект может быть также достигнут за счет использования различных материалов для формирования р—п-гетероперехода, в котором я2 изменяется по обе стороны перехода (смотрите дополнение 10.А).