Оже-рекомбинация
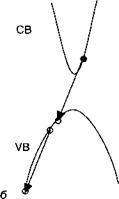
Процессом, обратным ударной ионизации, является Оже-рекомбинация. В этом случае электрон и дырка рекомбинируют, а высвобождаемая энергия передается другому электрону или дырке. Схематично для сильно упрощенной зонной структуры эти процессы иллюстрирует рисунок 6.Г. 1.
Рассмотрение эффекта в случае слегка более реалистичной зонной структуры, включающей зоны легких и тяжелых дырок, привело бы к увеличению числа возможных Оже-процессов за счет того, что второй дыркой могла бы быть либо легкая, либо тяжелая дырка, при этом одновременно возможны были бы процессы как в той же самой зоне, так и между различными валентными подзонами.
Равным образом рис. 6.Г. 1 показывает, каким образом законы сохранения полной энергии и импульса ограничивают комбинации возможных начальных и конечных состояний. Например, рекомбинация электрона на дне зоны проводимости и дырки в вершине валентной зоны не является разрешенным Оже-процессом, так как вторая частица не может совершить вертикальный переход.
Качественно также очевидно, что поскольку в Оже-процессе участвуют 3 частицы, он должен превалировать в условиях повышенной концентрации электронов и дырок. Как правило, это имеет место в случае узкозонных полупроводников или в системах с сильным отклонением от термодинамического равновесия (например, при больших уровнях оптической накачки или инжекции тока, как это имеет место в полупроводниковых лазерах).
 Единственной моделью, которая дает надежду получить аналитическое описание Оже-рекомбинации (и тем самым дать некую физическую интерпретацию), является модель с двумя параболическими зонами, электроны и дырки которых обладают эффективными массами соответственно тс и mv. Предположим, что электроны могут достичь равновесия друг с другом, а дырки могут сделать то же самое в течение времени, меньшего характеристического времени рекомбинации. Мы предположим также, что распределение частиц остается невырожденным. В этом случае концентрация электронов определяется соотношением:
Единственной моделью, которая дает надежду получить аналитическое описание Оже-рекомбинации (и тем самым дать некую физическую интерпретацию), является модель с двумя параболическими зонами, электроны и дырки которых обладают эффективными массами соответственно тс и mv. Предположим, что электроны могут достичь равновесия друг с другом, а дырки могут сделать то же самое в течение времени, меньшего характеристического времени рекомбинации. Мы предположим также, что распределение частиц остается невырожденным. В этом случае концентрация электронов определяется соотношением:
СВ
VB
А
Рис. 6.Г.1. Два возможных процессов Оже-рекомбинации: (а) электрон с импульсом к1 рекомбинирует с дыркой кА, а другой электрон с к2 получает высвобожденную энергию и переводится в состояние к3 (СНСС); (б) аналогичный процесс с участием двух дырок и одного электрона (СННН).
|
)-ц„ + ес(кг)~ М*+М,- £Лк„) |
|
И вновь отметим, что этот процесс должен быть разрешен законом сохранения импульса, т. е.: К. + Ц-к^Ц (6.Г.6) Атакже законом сохранения полной энергии: £,(*,)+ еХк2)-еХкн)= £с (к3) (6.Г.7 а) Таким образом: |
|
М,-Е, |
|
Р = ехр |
|
К„Т |
|
П2к2 |
|
£с(к)=Ес + |
|
2те ЕсЫ-М„ К„Т |
|
/с(к) = ехр |
|
В случае дырок аналогичное выражение имеет вид: Мр-еАк) |
|
/Дк) = ехр |
|
КлТ |
|
П2к2 2т„ |
|
£„ (к ) = Еу - |
|
/>(к1,к2,к3) = ехр |
|
КвТ 2Г 2 2 / 2 Ь кх + к2 + тс /ту)кь |
|
2 П р Лг>. |
|
Ехр |
|
2 тсквТ |
|
( |
|
Ес~Мп |
|
П - Nс ехр |
|
КвТ |
|
|
|
|
|
|
|
|
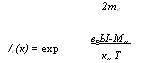 |
|
|
|
 |
|
|
|
|
|
|
|
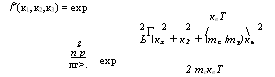 |
|
|
|
— !сх+кг{тс/т№ -кг2]+Ее = 0 2/и,
Таким образом, взаимодействие слабо зависит от кр к2, кЛ, наиболее вероятный процесс определяется максимизацией Р(кр к2, &л), при этом константы определяются законами сохранения.
Для того, чтобы найти максимальное значение, используем ту же процедуру, что и в дополнении 6.В, и используем метод множителей Лагранжа для нахождения максимума функции:
Р = Р(к„ к2, к„)~ Л-^-[[10]1 + *2 + (к / т„)кь - А:32^ 1 — А(б, +кг-кн - к3)
(6.Г.8)
Таким образом:
|
2-(У»-*,Г)-Л = 0 (/> - т*я7’)+ Я = 0 |
|
2 тскпТ Н2к- |
|
Э£ Дк2 Э/7 Дк. |
|
2тсквТ /и, 2тсквТ /я, |
|
■ {р - уквТ)~ Я = 0 ЭЛ, '' ^ |
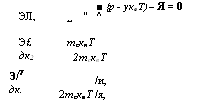 |
|
|
|
|
(6.Г.10) |
![]() При этом оптимальная величина имеет место при:
При этом оптимальная величина имеет место при:
К - к к - -—к т.
Закон сохранения импульса дает:
После того, как &2, &Л, къ определены в функции к{, эта последняя величина получается из закона сохранения энергии, что в результате дает:
|
П2к2 |
![]()
|
(6.Г.12) |
![]() Тс
Тс
> М= —
Таким образом, максимальная вероятность составляет:
|
ДГ2ДГ ^ * С х V |
|
П2р |
|
Р = |
|
Ехр |
|
+ цквТ 1 + 2ц Е% |
|
М„~МР КаТ |
|
П II /■--ехр |
|
Ехр |
|
+ц квТ |
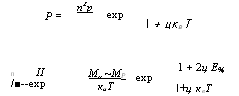 |
|
|
|
|
|
|
|
Вероятность Оже-рекомбинации (СНСС)
Это позволяет определить максимальную вероятность при термодинамическом равновесии в виде:
|
(6.Г.14) |
![]() 1 + 2 М Еі + ц квТ
1 + 2 М Еі + ц квТ
«Зеркальный» процесс, в котором участвуют две дырки и один электрон может быть получен заменой 1///, N <-> N что дает:
|
Мп-Мр КвТ |
|
-ехр |
|
Ехр |
|
N. |
|
1 +цквТ Вероятность Оже-рекомбинации (СННН) |
|
(6. Г. 15) |
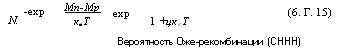 |
|
2 + /* Е8 1 +М квТ |
|
>снн _ Р ° " N. |
|
Ехр |
|
|
|
ОСНСС — Г п2 п Я СННН = Г *27)2 А ^СИССП А '"СНННпР |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сі« А7 |
|
= яс |
|
Пр - я, ^2 |
|
Вс =в0с — пп |
|
|
|
Сложна и не сопровождается особой дополнительной информацией с учетом того, что реальная зонная структура лишь в первом приближении может быть представлена двухзонной моделью. Таким образом, здесь мы не будем ставить себе целью определение этих величин. Тем не менее мы представим уравнение Б. Л. Гельмонта, (ЖЭТФ 48, 268 (1978)) для времени жизни электрона г = п^Я? ясс в условиях термодинамического равновесия: |
|
Оценка коэффициентов С |
|
СНСС’ СННН |
|
|
(4 7ге У Ь.3 |
|
Е'тг |
|
КаТ |
|
1/2 |
|
(1 + 2//) |
|
(6.Г.21) |
|
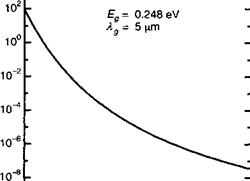
Рисунок 6.Г.2 показывает, что время жизни электрона в собственном полупроводнике с малой шириной запрещенной зоны сильно зависит от температуры из-за вероятности Р0 в уравнении (6.Г.14). Вдали от состояния термодинамического равновесия, как показывает ограниченное расширение (6.Г.20), скорость г”1, связанная с Оже-процессом, характеризуется квадратичной зависимостью от концентрации носителей, т. е. г-1 = САивегя2. При этом коэффициент пропорциональности соответствует коэффициенту Оже. Рисунок 6.Г. З показывает экспериментальные значения коэффициента Оже, определенные при комнатной температуре в двух случаях, важных для инфракрасного де- |
 |
 |
|
|
|
|
|
Со |
|
О |
|
100 150 200 250 300 Температура (К) |
![]()
|
Рис. 6.Г.2. Рассчитанное время жизни электрона в собственном полупроводнике с малой шириной запрещенной зоны £. Использованные параметры относятся к 1пАз(1 _х) с х = 15%. 0 100 200 300 400 500 600 700 Ширина запрещенной зоны (МэВ) |
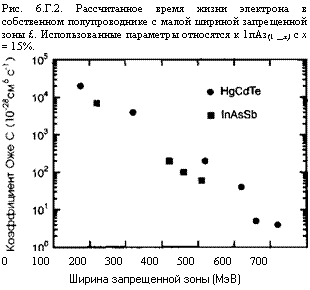 Рис. 6.Г. З. Коэффициент Оже для ЩСсЛГе и 1пА$8Ь при комнатной температуре в функции ширины запрещенной зоны (с вариациями ширины запрещенной зоны, определенными модификацией состава твердого раствора).
Рис. 6.Г. З. Коэффициент Оже для ЩСсЛГе и 1пА$8Ь при комнатной температуре в функции ширины запрещенной зоны (с вариациями ширины запрещенной зоны, определенными модификацией состава твердого раствора).
Тектирования: Н^Сс^ _ хТе и 1п Аб1 _ х8Ьх. Ширина запрещенной зоны в этих двух важных системах твердых растворов является функцией их состава х. Рисунок 6.Г. З подтверждает экспоненциальную зависимость коэффициента Оже от ширины запрещенной зоны.