Оптоэлектроника

Относительная интенсивность шума (RIN) и баланс оптической связи

Для того, чтобы определить амплитуду шума в лазерных диодах, являющегося след­ствием флуктуаций силы Ланжевена проведем разложение (13.Ж.14я) и (13.Ж.14<?) аналогично тому, как это было сделано в дополнении 13.Е (смотрите (13.Е.7). По­скольку нас не интересуют флуктуации тока, мы можем положить в этих уравнени­ях SJ = 0, что приводит к:

0ft> + r„V« + G0Ss = F„

(13.Ж.18)

Г Gns0Sn + (ш + Г5 )& = Fs

Здесь Fn и Fs есть Фурье-образы ланжевеновских сил. Напомним, однако, что эти Фурье-образы не обладают математическим существованием сами по себе, но явля­ются промежуточным шагом в расчете, как это было уже показано в дополнении 4.Г. Лишь параметры

= (г, г;)д/ = 2ДИД/ и (fM) = (ДЛ')л/ = 2Я„„Д/

В действительности определены и представляют собой мощность шума в поло­се А/

Система уравнений (13.Ж.18) может быть сразу решена, что дает:

ЦS = г<^9.£ +2{lь),t (13.Ж.19)

ь)R - О) )+ 2й)Гя

Дисперсия (SsSs*) величины Ss может быть получена в виде:

Здесь релаксационная частота coR и коэффициент затухания Гк уже были введены соответственно в (13.Е.12) и (13.Е.13).

Определим отношение дисперсии (Ss2) и s02 как относительную интенсивность шума (RIN). Величина RIN соотносится с (13.Ж.20) в соответствии с соотношением:

(13.Ж.21)

С учетом выражения для дисперсии (13.Ж. 15) выражение для RIN может быть за­писано в виде:

^spon (<Ц2 + Г„2)+ (ГC'g0s0 У (l + Ns / /?spo„ s„) Д0 (<y* - А>2У + (2а)ГяУ

Относительная интенсивность шума или RIN для лазерного диода

Размерный анализ этого отношения показывает, что RIN выражается в едини­цах Гц, что согласуется с определением (13.Ж.21). Поскольку эта величина, как правило, мала, принято выражать ее в дБ Гц-1. Относительные флуктуации интен­сивности (Ss2)/s2 в полосе А/могут быть получены из формулы:

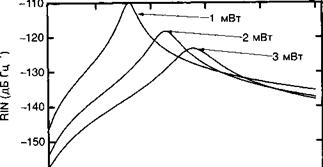
Таким образом, RINdB для — 160дБ Гц-1 соответствует RIN величиной 10-16 Гц-1. Рис. 13.Ж.2 показывает результаты расчета RIN с использованием уравнения (13.Ж.22). Параметры, использованные в этих расчетах для типичного лазерного диода, используемого в телекоммуникационных применениях, представлены в таб­лице 13.Е.1. Несколько моментов, следующих из полученных результатов, заслужи­вают внимания:

• шум максимален в резонансе, что является также и общим результатом теории электрических цепей;

• шум ослабляется по мере возрастания тока инжекции и лазерной мощности;

• уровень шума резко падает при малых частотах модуляции.

Интересное предельное условие для RIN имеет место при очень низких частотах модуляции (со = 0) и больших плотностях фотонов s0 (dg0sQ » ytot и для Rsps0 » nsyiot):

(13.Ж.226)

Мы напоминаем, что здесь г есть время жизни фотонов в резонаторе. Для ти­пичных параметров лазерных диодов, приведенных в таблице 13.Е.1 мы нахо­дим, что при мощности излучения 1 мВт величина RIN составляет 2 х 1,7 х 1012 с-1 х х (1,6 х 10"12 с)2/3,6 х 104 = 2,4 х 10~16 Гц'1 или -156 дБ.

Параметр RIN является существенным для расчета оптического бюджета в те­лекоммуникационных применениях. Ток /(0, генерируемый в фотоприемнике ла­зерным сигналом P(t) дается (11.18) или (11.41):

(13.Ж.23)

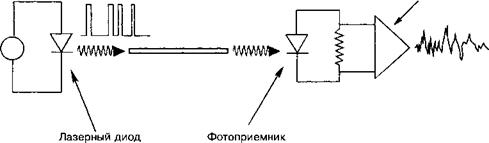
Здесь т/ есть полная эффективность с учетом потерь в оптической линии связи и фотоприемнике (смотрите рис. 13.Ж. З). Флуктуации P(t) также приведут к флукту­ации полного тока диода. С учетом соотношения пропорциональности (13.Ж.23) относительная дисперсия (Ai(t)2)/i02 тока идентична относительной дисперсии сиг­нала (P(t)2)/P2 от лазерного диода. Как мы уже показывали при рассмотрении ряда случаев (смотрите дополнения 4.Г и 11.А), дисперсия временных флуктуаций и частотный спектр флуктуаций Sp(f) (т. е. средняя мощность шума в частотном интервале А/) связаны соотношением:

F+bf

(AP(tj)= jAP(tfdt= J Sp(f)df = Sp(f)Af (13.Ж.24)

/

Это соотношение позволяет связать дисперсию шума фотоприемника с RIN лазер­ного диода:

RIN = <А/(/)2) = МО = = S. if)

In&f in Pi Sn

Таким образом, при расчете оптического бюджета (13.Ж.25) позволяет рассчи­тать шум фотодетектирования при приеме сигнала, обусловленный лазерным дио­дом. RIN лазерного диода следует сравнить с другими компонентами шума, обус­ловленными самим фотоприемником (с использованием концепции обнаружитель - ной способности, рассмотренной в дополнении 11.Б), а также оптическим волокном (поляризационный шум, шум усиления и т. д.)

Рассмотрим лазерный диод с приборными параметрами, приведенными в таблице 13.Е.1. В предположении мощности излучения jP0 = 3 мВт и частоте модуляции 1 ГГц (Д/= 109 Гц) лазерный диод будет обладать RIN, равным —150 дБ (смотрите рис. 13.Ж.2). Если полная эффективность линии связи составляет rj = 0,1, то фото­ток /0 составит:

Р0 Л Зх10‘3Вт

’ JKvJ) ’ ~5ЛГ~ "

При этом относительная амплитуда флуктуаций тока фотоприемника в этом случае составит:

Л/(д7о01) = /„(10-5 X 109)1

Это означает, что величина дисперсии составляет 10~3 х /0 или 3,7 х 10~7 А. Литература

G. P. Agrawal and N. K. Dutta, Long Wavelength Semiconductor Lasers, Van Nostrand Reinhold, New York (1986).

C. H. Henry, IEEE J. Quantum Electron. QE18, 259 (1982).

C. H. Henry, IEEE J. Quantum Electron. QE19, 1391 (1983).

У/2