Оптическое взаимодействие между волноводами: электрооптические переключатели
В разделе 9.3 мы видели, что электромагнитная волна, захваченная слоем сердцевины волновода обладает затухающей компонентой в ограничивающем слое (смотрите рис.
8.4) . Если поблизости от первого волновода располагается второй волновод, способный ограничивать волну той же самой частоты, при этом перекрытие с затухающей компонентой волны значительно, то ограниченная волна будет переходить через ограничивающий слой во второй волновод. Этот эффект аналогичен электронному туннелированию через барьеры в квантовой механике. Формализм связанных мод особенно хорошо приспособлен для описания связи этого типа между волноводами.
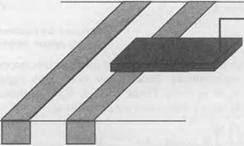
Рассмотрим два волновода (смотрите рис. 9.А.1). Первый (правый) волновод содержит слой сердцевины с показателем преломления пк, помещенный между двумя ограничивающими слоями с коэффициентом преломления п. Второй волновод, расположенный на расстоянии й налево от первого, содержит слой сердцевины с коэффициентом преломления пь, расположенным между слоями того же барьерного материала, что и правый волновод. Два волновода были изготовлены так, что если бы они были разделены бесконечным расстоянием, каждый из них обладал бы единственной основной собственной модой, обладающей компонентой электрического поля вдоль Оу, при этом каждая из компонент Ея(х, я, /) и Е^х, ъ 0 были бы решениями уравнений типа (9.13) вида:
|
2 |
![]()
|
2 |
![]() (9.А.1)
(9.А.1)
При приложении друг к другу каждый из волноводов будет действовать возмущающим образом на другой волновод.
|
Стационарной теории возмущений в квантовой механике (смотрите, например, дополнение 1.Б), мы можем записать новые моды для связанной системы в виде линейной комбинации фун- |
|
Следуя принципам, изложенным в разделе 9.4 и идентичным тем, которые были получены в рамках |
 |
|
|
|
|
|
|
|
![]()
![]()
![]()
![]()
|
В |
![]()
![]()
|
Г |
![]() Рис. 9.А.1. Геометрия связанных волноводов (а). Волна, локализованная исключительно в левом волноводе (б). Волна, связанная в двух волноводах (г).
Рис. 9.А.1. Геометрия связанных волноводов (а). Волна, локализованная исключительно в левом волноводе (б). Волна, связанная в двух волноводах (г).
Даментальных собственных мод для каждого изолированного волновода (так же как это было в случае квантовых ям, мы будем пренебрегать модами более высокого порядка):
Е{х, г, /) = + AL(z)EL(z)e'(M-f‘z) + к. с.] (9.А.2)
2
Если волноводы бесконечно отдалены друг от друга, амплитуды AR(z) и AL(z) являются константами. Приближение двух волноводов до минимального зазора индуцирует обмен энергией между ними, приводя к изменению амплитуд Ar(z) и Al(z).
Для правого волновода возмущением /wper будет поляризация левого волновода из-за синхронного возбуждения нового поля Е(х, z, 0, определяемого (9.2) или:
Z, t)= £•(,[nl (х)- я2 ]Ј(x, г, /) (9.А. З)
Здесь: nL(x) есть функция, равная nL в левом волноводе и я в других точках.
При рассмотрении задачи о распространении волны в одном направлении уравнение связанных мод может быть записано в виде:
_____ ^ _ 1(О£0
Эг 4 р0
J k (*)- n2][AR(z)El (x)ei(“-'fe)]dx +
Левый
Волновод (9.А.4)
+ |к2(^)-«2]к(^К(х)£л(х)е^>]с1х
Левый
Волновод
В формуле (9.А.4) первый член в интеграле с правой стороны не играет особой роли. Его влияние ограничивается малой коррекцией константы распространения @К. В то же время, второй член обеспечивает связь между двумя волноводами. В этом случае уравнение (9.А.4) и его эквивалент для левого волновода приобретают вид:
'ТГ‘АЯ=
Э* (9.А.5)
Здесь мы ввели фазовый сдвиг Д/? между двумя волноводами, определяемый:
(9.А.6)
А также интегралы перекрытия между двумя волнами, определяемые соотношениями:
|
Полновол |
![]() (9.A.7)
(9.A.7)
|
4p, |
![]() J[n2(x)-n2]EL(x)E/t(x)dx
J[n2(x)-n2]EL(x)E/t(x)dx
О правый волновод
Уравнения (9.А.5) являются классическими уравнениями связанных маятников, и они полностью эквивалентны уравнениям Раби, обсуждавшимся в дополнении 1.Д. Эти уравнения могут быть решены при введении пробных функций вида еы'. Предположим, что амплитуды на входе каждого волновода равны А£(0) = А0 и
В случае симметричных волноводов мы предположим, что gRL = gLR = g. Решения (9.А. 5) могут быть записаны в виде:
Ая{і)= Аь—&^Рі,2) вігі уі і?
^/.(0 = Ле~і(л^/2) + І
При этом:
![]()
|
/л(^)= Рйуг*лпг(у1) |
![]()
|
Уровни оптической мощности в волноводах в этом случае равны: |
![]() (9.А.9)
(9.А.9)
(9.А. 10)
= Ро ~ ри(г)
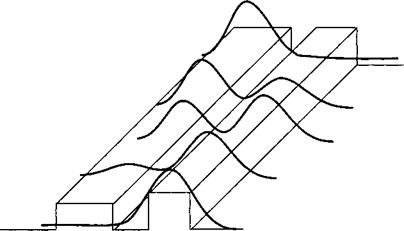
Здесь Р0 мощность излучения, падающего на вход левого волновода. Уравнение (9.А. 10) богато информацией. Во-первых, оно показывает, что энергия волны осциллирует между двумя волноводами по всему расстоянию распространения с пространственным периодом Л1гап5, называемым расстоянием переноса (смотрите рис. 9. А. 2), определяемым соотношением:
(9.А.11)
|
2 п
|
В дополнение к этому максимальная доля энергии, которая может быть перенесена из одного волновода в другой, составляет:
Так же, как это было и в случае осцилляций Раби, нас не удивляет то, что энергия может полностью перераспределяться между волноводами в процессе осцилляции, пока фазы согласованы, т. е. до тех пор, пока:
|
Рис. 9.А.2. Мощность волны распространяется и распределяется между двумя связанными волноводами. Расстояние, на котором осуществляется перераспределение мощности, есть расстояние переноса Лхпт. |
|
|
|
(9.А.13) |
![]() Afi=fiL~fiR = 0
Afi=fiL~fiR = 0
Условие согласования фаз между двумя волноводами
![]() Таким образом, волноводы могут выполнять функцию оптических переключателей (тем более тогда, когда они идентичны). Рассчитаем константу переноса к для двух ТЕ0-волн и случая, когда пк = п1 = я,. Поля Е^х) и Ек(х) определяются (9.16). Интегралы перекрытия (9.А.7) могут быть легко рассчитаны:
Таким образом, волноводы могут выполнять функцию оптических переключателей (тем более тогда, когда они идентичны). Рассчитаем константу переноса к для двух ТЕ0-волн и случая, когда пк = п1 = я,. Поля Е^х) и Ек(х) определяются (9.16). Интегралы перекрытия (9.А.7) могут быть легко рассчитаны:
(9.А.14)
BL есть амплитуда волны в левом волноводе, центр которого принят за точку отсчета (это объясняет, что интеграл берется от —d/2 до d/2), а Лк есть амплитуда затухающей волны, исходящей из правого волновода. Напоминаем, что электрические поля Е(х) изменяются в двух волноводах как cos (ах) и как q~kx — в ограничивающих слоях. Эти амплитуды приведены в (9.21), что дает:
G = A___ У' ___ а_ e-k0 (9.А.15)
Mcff а2 + к2 d + 2/к
Изменение q~kD оправдывает определение константы к как константы фотонного туннелирования между двумя волноводами.
Пример--------------------------------------------------------------------------------------------------------------
Рассмотрим два волновода со слоями сердцевины на основе InGaAs (я, = 3,5) и ограничивающими барьерными слоями на основе InALAs (п2 = 3,3). Ширина волноводов составляет 0,6 мкм. Коэффициенты а и к получаются с использованием программы MATHEMATICA, приведенной ниже:
Lambda = 1.55=0.6;(*micron*))
N1=3.5;n2=3.3;
K=2*N[Pi]/Lambda;
Bet=2*N[Pi]*neff/Lambda; alpha=Sqrt[(n 1 ~2*ВеГ2]; kappa=Sqrt[(-n2~*k''2+Ber2)];
Plot[fct,[neff, n2,n1}]; sol=FindRoot[fct= = 0,[neff,3.43}]; alpha /.sol(microrT-1*) kappa/. sol((microrT-1 *)
Из этих расчетов мы получаем а= 2,97 мкм“1 и к = 3,67 мкм“1. Если два волновода разделены расстоянием 1 мкм, коэффициент связи удается формулой (9.А. 16) и составляет 4,6 х 10_3 мкм-1. Таким образом, длина переноса itrans по порядку величины составляет 27r/g= 1,3 мм.
Этот механизм переноса энергии между связанными волноводами используется в элек - трооптических модуляторах, как это иллюстрируется рис. 9.А. З. В рассматриваемом случае два идентичных волновода изготавливаются с использованием электрооптичес - кой сердцевины с коэффициентом преломления, изменяющимся в зависимости от напряженности приложенного поля в соответствии с соотношением:
|
(9.А.16) |
![]() Д/i = n3rF
Д/i = n3rF
Здесь г — электрооптический коэффициент, в типичном случае равный нескольким пм В“1 в полупроводниках (г = 1,6 пм В“1 и пъг — 59 пм В“1 в СаАБ), при этом изменение Дя величиной 5 х 10“4 может быть легко получено при полевой модуля-
|
|
|
|
|
/ Связанные Волноводы |
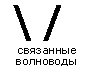 Рис. 9.А. З. Схематическое представление электрооптичес - кого модулятора, основанного на связанных волноводах.
Рис. 9.А. З. Схематическое представление электрооптичес - кого модулятора, основанного на связанных волноводах.
Ции амплитудой 100 кВ см. Длина волновода выбирается таким образом, что при нулевом электрическом поле (два волновода идентичны и А/3 = 0) вся энергия левого волновода передается в правый волновод у конца обоих волноводов, т. е. при gL = л/2. На левый волновод наносится металлический электрод для того, чтобы при приложении электрического поля Р происходило изменение как коэффициента преломления, так и константы распространения /?. Это приводит к фазовому сдвигу между двумя волноводами А/?(/). Мощность выходного излучения на выходе правого волновода в этом случае является функцией электрического поля, определяемой (9.А. 10) или:
|
2 |
Т!1 + |
Г 1 |
Л'/2- |
|
_21 |
К |
1 _ |
|
/,(*■) |
|
(9.А.17) |
![]()
Мощность оптического излучения будет практически полностью перенесена в левый волновод (1К(Ь) = 0) при приложении достаточно сильного электрического поля Р, такого что:
|
Подложка |
|
1пР |
|
1пР (р+) |
|
Полосковый волновод 6а1пАвР (Л = 1,3мкм) |
|
Волновод 6а1пА8Р (Л. = 1.3 мкм) |
|
Усилительная секция 6а1пАвР {Л -1,5 мкм) |
|
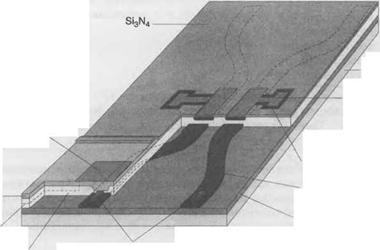
Рис. 9.А.4. Реализация переключателя на связанных волноводах. Это схематичное представление показывает переключатель 2x2, интегрированный с оптическим усилителем. (С разрешения N УосЦёапу @ЬСЯ/ТНАЬЕ5). |
|
Имплонтация н+ 1пР п. Ш. |
|
|
|
|
|
|
|
|
 |
|
|
|
(9.А.18) |
![]() LbЯ{F)=Sn
LbЯ{F)=Sn
Для оценки необходимой напряженности поля мы можем грубо предположить, что изменение коэффициента преломления AnL, определяемое (9.16), влияет на константу распространения как ЯL = 2meffl (мы напоминаем, что Л0 есть вакуумная длина волны и neff есть эффективный коэффициент преломления в волноводе) так, что AЯ = 2яАп/Л^. В этом случае условие (9.18) определяет напряжение переключения при условии, что Anc{f(F) = (V3/2)(A0/L). При длине волновода 2 мм и длине волны 1 мкм нам необходимо обеспечить изменение Ап величиной 4 х 10"4, что соответствует полю переключения 100 кВ см-1 или 10 В для волновода толщиной 1 мкм. Рисунок 9.А.4 иллюстрирует реальную реализацию такого электрооптического модулятора. Поскольку для функционирования этого прибора не требуется перемещения зарядов, емкостные эффекты в действительности дают нулевой вклад, и времена переключения крайне малы. Максимальная частота модуляции для этого типа приборов превышает 10 ГГц.