Оптоэлектроника

Оптическое усиление в квантово-размерной структуре: общий случай

В предыдущем разделе мы видели, что пороговый ток в значительной степени про­порционален толщине активной области лазерного диода (т. е. ширине потенци­альной ямы, сформированной двойным гетеропереходом). Для дальнейшего умень­шения порогового тока, естественно, необходимо еще более уменьшать размер ак­тивной области вплоть до шкалы квантовых размеров (т. е. использовать потенциальные ямы, которые настолько узки, что они способны ограничивать и квантовать движение носителей в направлениях, перпендикулярных границам раз­дела). Какое-то время мы уже посвятили исследованию физики таких квантовых ям в главе 8. Напомним теперь некоторые важные результаты этой главы.

Электронные и дырочные волновые функции в квантовых ямах определяются произведением трех членов: периодической части блоховских волновых функций, обусловленных тем фактом, что носители принадлежат экстремумам конкретной полупроводниковой зоны (нс(г) для электронов, иу(т) для дырок при к = 0 в случае модели с одной валентной подзоной с экстремумом при Г); части, описывающей свободное движение носителей параллельно границам раздела квантовых ям (е{к«г", где Гц и к^есть соответственно положение и волновые векторы волны в плоскости квантовой ямы); части, описывающей квантование движения в направлении, пер­пендикулярном гетерограницам. Таким образом, волновые функции электронных состояний в подзоне п и тяжелые дырочные состояния в подзоне т могут быть записаны в виде:

|еи(к,)> = мс(г)е1к'г>б? п(г)

ИЛЦ)) = мДг)е“‘,г,/г/гт(г)

Огибающие функции еп(г:) и /г/гт(г) описывают одномерные состояния с энерги­ями еп и ккт и являются решениями одномерных уравнений Шредингера:

— + >/Дг)|е„) = е„|е„) 2тг

(13.39)

2ти

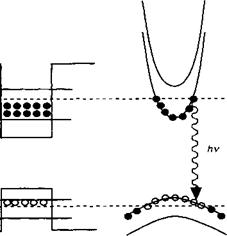
Здесь К(г) и У^(1) есть потенциалы электронов и тяжелых дырок (смотрите рис. 13.18). Напоминаем, что на таких диаграммах увеличению энергии соответствует направление вверх для электронов и вниз — для дырок. Эта концепция может быть расширена на случай подзоны легких дырок спин-орбитальной подзоны, что вызы­вает существенное усложнение необходимых обозначений (в связи с этим в насто-

Е( к)

Плотность состояний

Е.

/7/7

/7/7 2

Рис. 13.18. Зонная структура, подзоны ДЦ) и плотности состояний в квантовой яме.

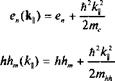Ящей главе мы не будем рассматривать такие подзоны). Уравнения (13.38) и (13.39) показывают, что электроны и дырки распределены по энергетическим подзонам (которые, в дополнение ко всему, смещены параллельно друг к другу для различ­ных типов носителей), Экстремумы этих подзон (еп и ккт) определяются уравнени­ями Шредингера (13.39) и их положение составляет (смотрите рис. 13.18):

(13.40)

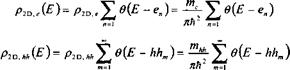Плотность состояний в каждой подзоне постоянна, означая, что концентрации электронов и тяжелых дырок есть (смотрите (8.41а, б):

(13.41)

Здесь 0есть функция Хэвисайда.

Межзонные оптические переходы соединяют СОСТОЯНИЯ С идентичными кц. Та­ким образом, фотон с энергией ку соединяет состояния в подзоне проводимости п с состояниями в валентной подзоне т, связанные соотношением:

(13.42)

Здесь тг есть приведенная эффективная масса, определяемая /тг = 1 /тс + 1 /ткк (смотрите рис. 13.18). В такой системе оптическое усиление для электромагнитной волны с частотой п было рассчитано в разделе 8.7. Оно было получено суммирова­нием вкладов из-за оптических переходов между валентными подзонами т и под­зонами зоны проводимости п с волновым вектором, лежащим в интервале от к до к + йк. Это приводит к плотности инверсии носителей:

Й{Мс - ЛГ, Г = £2^{/ЛеЛ1с)]- f:EM }<!& (13.43)

С/

Усиление ^(/гV) может быть получено интегрированием по к вклада (13.43) в оптическую восприимчивость и суммированием по всем участвующим подзонам. Этот результат получен в виде соотношения (8.86), но здесь мы перепишем его в виде, более пригодном для настоящего обсуждения:

ГМ= «20 X '».Л/ЛМ - /ЛМИа,, - Е'-еК-Ы1т) (13.44)

Здесь / т есть интегралы перекрытия |(л|/я)|2, г/сп и /уш есть распределения Ферми в подзонах пит:

/ЛМ= 1

1 + ехр{[£;^у)-£,с]/*г} Е^у)=Ег+е„+^-(/IV - Е'-ея)

1 + ехр {[£;(Аі/)- Ег<]кТ } Е”(Иу)= - Ег - Мт)

Тг ту

Коэффициент поглощения а20 (см-1) есть поглощение квантовой ямы с ну­левой заселенностью (т. е. в условиях нулевого тока) и он определяется соотно­шением:

_ 2яд'х^т, (13.46а)

Здесь Л0 есть длина волны в вакууме. Как это уже достатоно подробно обсуждалось в разделе 8.7.2, (13.46с) представляет коэффициент ослабления для света при нор­мальном падении, проходящий через квантовую яму толщиной с1. Таким образом,

Коэффициент а2В выражается в единицах см-1. Концепция длины ослабления в кван­товой яме не является особенно удовлетворительной. Поскольку толщина кванто­вой ямы очень мала по сравнению с длиной ослабления 1 /а2Г>, ослабление, опреде­ляемое с1а20, не зависит от толщины квантовой ямы (строго говоря это имеет место, если только в квантовой яме имеется единственный локализованный уровень). В связи с этим используем скорость ослабления в расчете на одну яму (безразмер­ную величину) А20 = (1а20, определяемую (8.866):

А _ 2лд2х1тг (13.466)

20 ~ * +2

Коэффициент ослабления для одной квантовой ямы

Эта формула подразумевает использование впечатляюще больших параметров. Для того, чтобы выразить Ат через параметры близкой величины, введем два следу­ющих энергетических параметра: межзонную энергию Еус = Н ку*/2тг, где кус есть волновой вектор кус = 2л/хус, и электростатическую энергию Ев1а1 = #2/4ле0А0. В этом случае скорость ослабления принимает вид:

Это последнее уравнение позволяет быстро оценить скорости ослабления в кванто­вых ямах с использованием параметров аналогичной величины. Следующий ниже пример иллюстрирует удобство использования указанного выражения.

Пример ---------------------------------------------------------------------------------------------------------

Рассмотрим скорость ослабления для квантовой ямы на основе GaAs. Напомним используемые параметры для GaAs:

Т = 0,067т ; т = 0,46т ; т = 0,058т

TOC o "1-5" h z с ’ e’v ’ е’г ’ е

Xw = 6,14 E/V2 = 4,3 Е (смотрите таблицы 7.1 и 8.1)

П = 3,3

SC 7

Л0 = 0,8 мкм

Уравнение (13.466) приводит к коэффициенту ослабления:

2;r(l,6x 10'19 Кл)2(4,3х 10~'° м)2 х0,058х0,9х Ю~20 кг псо/

A2d — . ч ~ 0,о%

0, 8 хЮ-6 м х 3,3 х 8,85 хЮ"12 Фм‘‘ х (l,05 х 10“34 Дж с2)

Этот расчет, мягко говоря, утомителен! Все, что это в действительности означает, так это то, что единицы системы MKSM не приспособлены идеально для решения по­добных задач. Это, в свою очередь, является еще одним поводом для того, чтобы переписать (13.47) с использованием более легко манипулируемых параметров. Оп­ределив Evc = 3,99 эВ и Estat = 1,8 мэВ, мы легко получаем тот же самый результат.