Оптическое усиление в диодах с гетеропереходами
В разделе 13.3 основное внимание уделялось спонтанному излучению. Однако в главе 7 мы видели, что в том случае, когда полупроводник выводится возбуждением достаточно сильно из состояния термодинамического возбуждения, становится возможным достижение инверсии заселенности между электронами в зоне проводимости и дырками в валентной зоне. Тогда мы даже сумели получить условие прозрачности, т. е. концентрацию заряженных носителей я1гапзр в зонах, необходимую для того, чтобы материал был эффективно прозрачен для излучения, и при превышении которой материал проявляет усиление (смотрите (7.69)). На языке тока электрической инжекции (13.3) это означает, что материал становится прозрачным, когда он возбуждается плотностью тока прозрачности /1п|П5р, определяемой:
|
^ iansp ^101 ] , р Мс 1/2 |
![]()
|
*1/2 |
![]() 1 = 0 (13.18)
1 = 0 (13.18)
Здесь: N и N есть соответственно эффективные плотности состояний в зоне проводимости и валентной зоне. При возбуждении выше этого порога прозрачности усиление будут испытывать фотоны с энергией /гц удовлетворяющей критерию Бернара—Дюррафура:
Е8 < к> <ЕЛ-Е» (13.19)
В контексте оптической восприимчивости усиление среды с усилением у(1гу) было
Рассчитано в разделе 7.3 при обсуждении скоростных уравнений. Эти результаты на
Столько важны, что мы должны воспроизвести их здесь. Усиление дается формулой:
У(ИV) = а0(й>[/,(ЛV)- /„(А V)]) (13.20а)
Здесь а0 есть поглощение пустой зоны проводимости (т. е. в условиях нулевого тока), определяемое выражением:
Напоминаем, что /с и есть функции Ферми—Дирака, определяемые (13.7), а хус есть матричный элемент, определяемый (7.11), тг — приведенная эффективная масса (7.13), я5с — коэффициент оптического преломления полупроводника, а Л0 — длина электромагнитной волны с частотой со в вакууме.
Уравнение (13.20а) может быть также записано в форме, которая лучше напоминает аналогичные уравнения для лазерных атомарных переходов, введенных в главе 4:
У(Л V) = Й1 (А V(Й V)- /,.(А V )] (13.20«)
Понятно, что в (13.20<?) множитель р](Иу)(/с — /) играет роль — Nl)в
Уравнениях для лазера на атомных переходах.
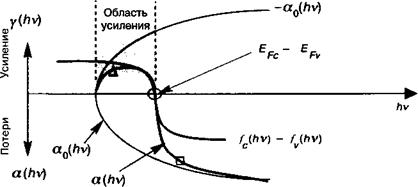
Таким образом, по мере того, как плотность тока /, протекающего через диод становится все более важной, увеличивается и концентрация носителей, определяемая (13.3). Это приводит к тому, что квазиуровни Ферми, определяемые (13.4), все больше и больше проникают в зоны, что приводит ко все большей и более широкой кривой усиления (13.20а) — смотрите рисунок 13.9. Рисунок 13.10 показывает
|
|
|
|
В
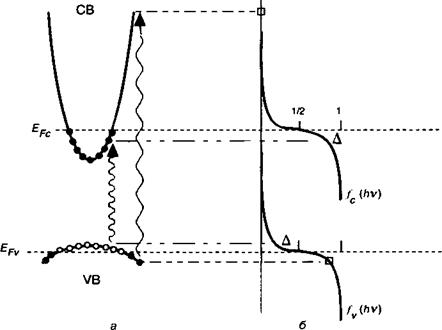
Рис. 13.9. Инверсия заселенности и оптическое усиление в полупроводниковой среде.
Этот рисунок иллюстрирует уравнение( 13.20) и представляет две зоны, участвующие в процессе (а). Рисунок (б) показывает соответствующие распределения Ферми—Дирака для квазиуровней Ферми в зоне проводимости и валентной зоне. Рисунок (в) показывает кривую усиления среды (сплошная жирная линия), являющуюся произведением коэффициента поглощения а0(Иу) (бледная линия) и коэффициента заполнения^ —/у (жирная линия). Символы Д и □ обозначают фотоны с энергией, соответственно удовлетворяющей и не удовлетворяющей условию Бернара—Дюррафура. СВ и УВ — соответственно зона проводимости и валентная зона.
|
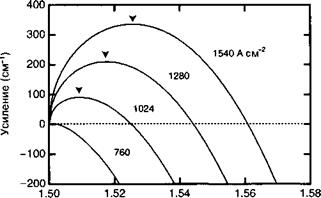
/?у(эВ) Рис. 13.10. Зависимости усиления от плотности тока инжекции для гетероструктуры ОаАБ/АЮаАБ толщиной 100 нм в предположении, что излучательное время жизни составляет 5 не при внутренней квантовой эффективности 0,5, что соответствует = 2,5 не. В данном случае плотность тока прозрачности составляет 760 А см-2. |
Результирующие кривые усиления для разных уровней тока инжекции. Как нам уже известно из раздела 7.7 и рисунка 7.7, максимальное усиление утах (являющееся одним из наиболее важных параметров этих кривых, поскольку лишь ближайшие к утах моды будут генерировать) возрастает практически линейно с увеличением концентрации носителей п в области выше порога прозрачности Общепринятым является использование для сложной зависимости у^ от п линеиной аппроксимации:
|
-1 |
![]()
|
= Го |
![]() (13.21)
(13.21)
Здесь: параметр у0 выбирают методом оптимального подбора. При концентрации п в диапазоне от 0 до я1гап8р среда является поглощающей. При п > п1гапвр материал становится прозрачным и зависимость утах от п хорошо воспроизводится.
Уравнение (13.3) позволяет нам переписать это выражение в виде зависимости от плотности тока Г. В этом случае максимальное усиление у дается выражением:
|
-1 |
|
= Го |
|
*^transp |
|
||
Здесь: плотность тока прозрачности определяется (13.18) и связана с ntransp соотношением:
77/*га d
Пример----------------------------------------------------------------------------------------------------------
Рассмотрим усиление, обеспечиваемое лазерным диодом на основе двойного гетероперехода GaAs/AlGaAs. Из экспериментов установлено, что время жизни из - лучательной рекомбинации tnd составляет 5 не. Из рисунка 7.7 следует, что пороговая концентрация носителей, соответствующая прозрачности «transp, составляет
1,2 х 1018 см-3. Предположим, что диод обладает квантовой эффективностью толщина его активной области й составляет 100 нм, ширина и длина соответственно равны 10 и 300 мкм. В этом случае пороговая плотность тока прозрачности / составляет:
1гапзр
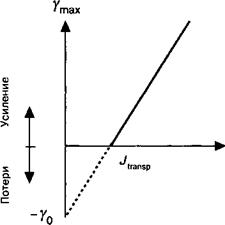
Рис. 13.11. Изменение максимального усиления полупроводникового перехода в функции плотности тока инжекции в рамках модели линейной аппроксимации.
|
J |
![]() •Лгатр = 1,6хЮ"19 КлхЮ"5 смх1,2х1018см 3 /(0,5х5х10~9 с)= 760 Асм 2 или 23 мА
•Лгатр = 1,6хЮ"19 КлхЮ"5 смх1,2х1018см 3 /(0,5х5х10~9 с)= 760 Асм 2 или 23 мА
При концентрации носителей п= 2,4 х 1018 см-3 (что соответствует уровню, вдвое большему порога, и току инжекции 46 мА) максимальное усиление составляет 300 см-1. Это приводит к усилению <7 в структуре величиной ехр(3 X 102 СМ"1 X 3 X 10~2 см) или 8100.
Полупроводниковые оптические усилители (80А) используются в качестве усилительных каскадов на выходе лазерных диодов (в этом случае их обычно называют монолитными оптическими усилителями — МОРА). В рассматриваемом случае одна из проблем заключается в том, чтобы они находились в режиме лазерной генерации. С этой целью для устранения обратной оптической связи на выходные окна наносятся антиотражающие покрытия (Я < 106). Более того для максимального извлечения энергии из этих приборов их резонаторам придается рупорная форма. Это делает резонатор нестабильным, что препятствует формированию стационарных оптических мод в спектральном диапазоне усиления (смотрите рисунок 13.12).