Оптическое ограничение
Представляется важным оценить количество энергии, эффективно каналируемой или захваченной волноводом между точками 0 и — й. Это количество энергии описывается с использованием коэффициента ограничения в, определяемого как:
|
|
Для того, чтобы ознакомиться с этой концепцией, рассчитаем коэффициент ограничения для моды т симметричного волновода. Благодаря симметрии задачи (9.27) может быть записано в виде:
2j|Ј„(xfdx
|
Г =1 |
![]()
|
(9.28) |
![]() О______
О______
Или с учетом (9.16) и (9.22):
|
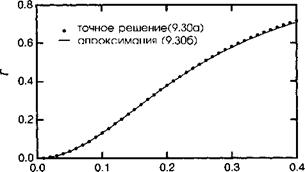
/ «1 V У Здесь X есть соотношение sin вт /sin вс и мы напоминаем, что Nm есть число допустимых мод волновода. Рис. 9.9 представляет изменение коэффициента ограничения для типичного волновода в функции sin вт /sin 0с. Отметим, что эта последняя величина возрастает с увеличением индекса моды, при этом, как видно из рисунка, максимальным ограничением при минимальном порядке моды. Таким образом, ТЕ0 и ТМ0 моды волновода испытывают наиболее эффективное волноводное распространение. Этот факт используется при конструировании многих оптоэлектронных приборов (например, лазеров, модуляторов и т. д.) Естественно, что разработчик волноводов будет предпочитать использование одномодовых волноводов. Ограниченное разложение (9.30я) приводит к крайне полезной аппроксимации для ТЕ0: ^ где D = -^^-д/л,2 - /122 (9.306) |
|
.2 . 2 V Sin 9С - sin ет I |
|
Г° 2+ D2 ’ |
|
(9.30л) |
|
Sin 2 <9 |
|
1 |
|
= 1 |
|
Г =1 |
|
1/2 |
|
1+^ЛГ |
|
1 + к - |
|
Л |
|
|
|
|
|
|
 |
|
|
|
|
|
|
Рассмотрим волновод, состоящий из слоя сердцевины на основе GaSb толщиной 0,2 мкм, а также из ограничивающих слоев AlGaSb. Пренебрежем собственной дисперсией этих материалов и примем я, = 3,837 для коэффициента оптического преломления GaSb и п2 = 3,589 для аналогичного параметра Al; GaSb. Числовая апертура NA волновода составляет, таким образом, 1,36. Число мод на длине волны
1, 55 мкм дается (9.6) и составляет N= Int(2 х 0,2 х 1,36/1,55) +1 = 1. Таким образом, рассматриваемый волновод является одномодовым, и мы можем использовать выражение (9.306) для определения коэффициента ограничения для ТЕ0-моды в волноводе. При этом мы получаем D = 1,10 и Г0 = 0,38.
Программа MATHEMATICA, приведенная ниже, позволяет сравнить значения коэффициентов ограничения, полученные с использованием точного метода (9.30я) и аппроксимации (9.306) применительно к описанной выше системе. Полученные таким образом результаты иллюстрируются рис. 9.9 и они подтверждают действенность аппроксимации (9.30б).
Lamda=1.55;t=.
N1=3.837;n2=3.589;ON=Sqrt{nr2-n2-2};
Ninit=(n1+n2)/2;
K=2*N[Pi]/Lambda;
Bet=2*N[Pi]*neff/Lambda;alpha=Sqrt[(n‘T2*k''2-Ber2)];
Kappa=Sqrt[(-n2''2*k''2+Bet''2)];
Fct=Tan[alpha*t]-2*kappa*alpha/(alpha''2-kapa~2);
Tab=Table[{,sol=FindRoot[fct,{neff, ninit}];
Gamma=Abs[1 -(n1 ~2-nefr2)/(n1 ~2-r2"2)/
(1+k*t/2*Sqrt[nefT2-n2])/.sol},{t,.01 ,.4,01}];
Plot1=ListPlot[tab]
Dis=2*N[Pi]*t*ON/Lambda;
Plot2=Plot[dis''2/(2+dis~2),{t,0,4}]
Show[plot1,plot2]