Оптоэлектроника

Оптические параметрические генераторы с двойным резонансом (йРОРО)

В рассматриваемом случае дополнительная волна (о2 также испытывает оптическую обратную связь от зеркал и уже не является пренебрежимо малой по сравнению с сигнальной волной сох. Таким образом, мы пришли к подтверждению формализма, представленного в дополнении 9. Г и использованного для описания распростране­ния оптической волны в резонаторе Фабри—Перо. Обозначим как гх и г2 (г. = (Я)112?* для I = 1,2) коэффициенты отражения двух зеркал (которые предполагаются иден­тичными на входе и выходе) соответственно для сигнальной и дополнительной волн. Введем вектор комплексной амплитуды А(г):

SHAPE \* MERGEFORMAT

А* (г)е>м

Распространение дополнительной и сигнальной волн между входным и выход­ным зеркалами, описываемое системой уравнений (12.45), может быть представле­но в матричной форме:

(12.53)

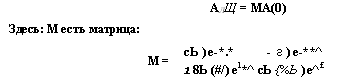Ал обозначает амплитудный вектор, распространяющийся направо. Как только волна приходит к выходному зеркалу, часть излучения отражается, что описыва­ется вектором:

АЛЬ) = КМА(0), при этом И =

Здесь: Аь соответствует комплексной амплитуде, направленной налево. Как и в предыдущем случае, сигнальная и дополнительная волна не могут взаимодейство­вать с волной накачки в этом направлении распространения, так как они не могут удовлетворять условию фазового согласования (12.42). В этом случае амплитудный вектор Аь перед отражением имеет вид:

Наконец, сигнальная и дополнительная волны отражаются у входного зеркала, при этом амплитудный вектор принимает вид:
Условие генерации может быть получено из требования, что сумма всех этих вкла­дов расходится, как это и было в предыдущем случае. Мы могли бы потребовать также, чтобы все эти волны идентично воспроизводились при z = 0 (условие, экви­валентное первому), т. е. что АЛ(0) = А(0). Это требование накладывает условие: (1е1(КЬКМ - И) = 0 (12.57) Здесь: Ы есть матрица тождества формата 2x2. Это последнее условие получается путем перемножения матриц, что приводит к выражению:
= 0	(12.58)
(12.59)
(12.60) Уравнение (12.59) дает нетривиальное решение только в том случае, когда удовлет­воряются следующие три условия:
К{Ь - = тп К2Ь - ф2 = пл
(12.61)
Первые два условия в (12.61) есть ничто иное, как условия стоячей волны в резонаторе для сигнальной и холостой волны. Третье условие показывает, что резо-

Натор устанавливает параметрические колебания для двух волн, как только пара­метрическое усиление для двух волн g превысит потери на зеркалах Я{ и Я'г Как и в случае простого резонатора, мы имеем cosh(gZ) « 1 + (gthresholdЈ)[25]/2 и Ях « « 15 где

^threshold есть параметрическое усиление у порога генерации. Это пороговое усиление дается соотношением:

Г™ L - V0 - Л. XI - ) (12.62)

Порог DROPO

Последнее приведенное выражение следует сравнить с условием (12.50) для резо­натора с простым резонансом. Конфигурация с двойным резонансом уменьшает порог генерации на коэффициент:

Р _ & threshold, простой резонанс & threshold, двойной резонанс

Пример ---------------------------------------------------------

Теперь мы рассчитаем порог генерации ОРО, описанного в разделе 12.6.1, т. е. для кристалла GaAs длиной 5 мм, согласованного по фазе с волной 9 мкм и накачива­емого пучком на длине волны 5 мкм. Оба торца кристалла на этот раз покрыты зеркалами с коэффициентом отражения 98 и 99,8% соответственно для сигнальной и холостой волн. Мы хотим найти пороговую мощность, необходимую, чтобы ини­циировать параметрическую генерацию в структуре.

Порог генерации уменьшается на коэффициент F' определяемый (12.63):

F = [2/(2х10-3)]1/2 илив31раз Таким образом, оптическая мощность у порога генерации есть:

^з, threshold =6/31 МВт см -2 или 190 кВт см _2

Теперь мы обобщим некоторые из особенностей, связанных с явлением пара­метрической генерации:

• Все пары частот (a)v со2), удовлетворяющие условию со{ + со2 = cov где со3 есть частота генерации накачивающего пучка, могут генерироваться ОРО. Конкрет­ный выбор пары частот, которая испытает эффект ОРО, определяется стационар­ными фазовыми условиями (12.49б) и (12.61) (для начала заметим, что резонатор - ные зеркала должны быть тщательно подобраны) и, в особенности, условием со­хранения импульса участвующих в процессе фотонов (12.42). Мы можем изменить пару (cov со2) и, таким образом, длины волн, генерируемых ОРО за счет изменения условий фазового согласования (например, изменяя ориентацию нелинейного кристалла). На практике ОРО используется как перестраиваемый источник излу­чения (смотрите дополнение 12.Б).

• Как это было в случае лазеров, параметрические колебания возникают из шума в резонаторе. Этот шум является следствием не спонтанной эмиссии, а квантового шума в резонаторе (смотрите раздел 2.5).