Оптические фононы и фрелиховское взаимодействие
Рассмотрим теперь, каким образом фононы влияют в материале на динамику носителей. Взаимодействия такого рода чрезвычайно важны как при рассмотрении явлений переноса (т. к. электронная подвижность при комнатной температуре определяется взаимодействием с фононами), так и при рассмотрении релаксационных явлений с участием носителей, которые возбуждаются оптически или сильными электрическими полями.
Фононы представляют собой колебательные волны атомов решетки. Для начала мы начнем с изучения простой модели, представляющей собой линейную цепочку двухатомных молекул. В качестве аппроксимации используем предположение о том, что межатомные силы линейно возрастают с увеличением смещения от состояния равновесия, при этом они направлены таким образом, чтобы возвращать атомы в положение равновесия при й/2 (рис. 6.Б.1).
Такая двухатомная модель очень удачно описывает бинарные полупроводниковые соединения, такие как ваАБ или 1пР.
Предполагается, что смещение атома у по отношению к его равновесному положению для тяжелых атомов (масса М) и легких атомов (масса т).
СУ
М к т к Лллл/Юлллм
Х, УI *уч 1 У у+1 ХуЧ2 У1+2.
Рис. 6.Б.1. Линейная цепочка из атомов с массами М и т. Межатомные силы пред
Ставлены на рисунке пружинками таким образом, что сила между прилегающими атомами составляет к(у] - х). При этом хи у обозначают расстояния смещения атомов от своих равновесных положений.
Классический гамильтониан такой системы представляет собой:
#(*,, Ур У^ = *'2 +тІЇ +к^і~хі) + (6Б1)
При этом сопряженные переменные имеют вид:
ЭЯ
|
(6.Б.2) (6.Б. З) (6.Б.4) |
![]() ЭЯ
ЭЯ
Г’>~~5Г~ т*‘
В этом случае динамическое поведение системы описывается уравнениями: Рх, = А/ *, = = - к(х1 - у,)- к:(*, - УМ)
ЭЯ
Ру, =тУ1 = = -*6о - *іУ кІУі - х/>|)
Таким образом:
М хі = к(уІ + у^-2х;) ту і = к{хі, х+хі-2у])
Приведенные выше выражения представляют собой уравнения Ньютона для смещения каждого атома.
Будем искать решения в виде волн с частотами со (> 0):
|
(6.Б.5) |
![]() Х. = X ехр(і#/</ - ісої) у. = У ехр(і#/</ - їсої)
Х. = X ехр(і#/</ - ісої) у. = У ехр(і#/</ - їсої)
Подставляя (6.Б.5) в (6.Б.4) и полагая со* = 2к/Ми со* = 2к/т, получаем:
|
1 + е" |
![]()
|
-У = 0 |
![]() (б>т ~0)2)Х - О),
(б>т ~0)2)Х - О),
|
+ 1 |
|
Х + {со1-со'У =0 |
|
|
|
|
Условие существования нетривиального решения дает частотные моды:
|
= 0 |
![]()
|
•2 ■ й'2 2 " |
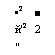 Т4 - (<у,, + а>1 )у2 + ща>1 віп
Т4 - (<у,, + а>1 )у2 + ща>1 віп
2 (ОХ. + сот, (О - — — ±
|
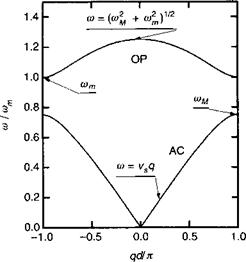
Рис. 6.Б.2. Дисперсионные зависимости для колебательных мод двухатомной цепочки, проявляющие акустические (АС) и оптические (ОР) ветви с их характеристическими пределами. |
Рисунок 6.Б.2 демонстрирует дисперсионные зависимости со (д). Отметим наличие двух ветвей, называемых ветвями оптических и акустических фононов.
В пределе при д —> 0 мы легко получаем:
|
Г~2к~ V, г7гес1 |
|
1 |
|
Ггп |
|
|
|
|
|
|
(6.Б.8)
|
Дсі |
![]() Дсі
Дсі
Т
А при д = к/й мы находим, что (оо^ = сот и соас = сом.
Приведенные выше решения лежат в пределах зоны, определяемой —п/й < д<п/й, поскольку решение для д = д0 +2лп/с1 представляет то же самое смещение, что и решение, соответствующее д0. В самом деле:
|
(6.Б.9) |
![]() Су = X ехр (і^оУ^ + 27rnj - ісоґ) = X ехр (і - і<у/)
Су = X ехр (і^оУ^ + 27rnj - ісоґ) = X ехр (і - і<у/)
Более того, если цепочка не является бесконечно длинной, а имеет конечную длину £ = Л# (см. также уравнение (5.10)), использование периодических граничных условий = х. и ум+. = у. приводит к дискретным значениям для д:
ДИс1 = 2т ■■
2
|
(6.Б.10) |
![]() Л
Л
<7„=Т -
В этом случае плотность мод для каждой ветви составляет Ц2л, а полное число мод равно 2И, т. е. равно числу степеней свободы в системе из 2#атомов.
Уравнение (6.Б.6) дает для каждого решения соотношение амплитуд X(д) и У(д), при этом в особом случае вблизи центра зоны (д ~ 0) для оптических фононов мы имеем:
|
М |
|
X =- |
|
1 + І |
|
Т |
|
|
|
|
А в случае акустических фононов:
|
V / |
(6.Б.12)
Таким образом, оптические фононы характеризуются противонаправленным движением двух типов атомов, что и объясняет их высокие частоты. В то же время акустические фононы не вызывают смещения пружинок при # —> 0 и таким образом не обладают упругой энергией (что и объясняет, почему их частота стремится к нулю в центре зоны).
Мы не будем изучать распространение модели нашей линейной цепочки на случай трехмерной кристаллической решетки. Необходимый в этом случае формализм потребовал бы внушительное число индексов для того, чтобы отследить трехмерные смещения каждого из атомов и их волновые векторы в зоне Бриллюэна. При этом сущность модели и в этом случае осталась бы неизменной. Для бинарной системы типа СаАз полное число мод становится равным 6УУ (где 2УУ есть число атомов в объеме V). Таким образом, решения распределены по трем акустическим ветвям с со(ц) —» 0 для ц —> 0 и трем оптическим ветвям, для которых *у(0) Ф 0.
Основным отличием одномерного и трехмерного случаев является существование мод, для которых смешения не являются параллельными волновому вектору ч — это поперечные моды. Рис. 6.Б. З иллюстрирует различные варианты смещений для волн, распространяющихся направо в симметричном случае (в любой решетке в общем случае смещения, связанные с модами, не являются параллельными или перпендикулярными волновому вектору).
Теперь возвратимся к одномерному случаю, который вплоть до настоящего времени рассматривался чисто классически. Для получения картины, более близкой к реальности, следует рассмотреть систему с точки зрения квантовой механики. Таким образом, мы должны заменить наше выражение для гамильтониана в (6.Б.1) на оператор гамильтониана, получаемый заменой р^ —> (й /ОЭ/Эх. и т. д. и при использовании коммутаторов [х, /?У ] = Ь и т. д. Однако более изящный путь заключается в трансформировании гамильтониана до введения операторов.
С этой целью давайте введем нормальные координаты:
|
|
(6.Б.13)
|
|
При этом обратное преобразование осуществляется с помощью соотношений:
|
Ч |
|
Я |
![]()
![]()
|
При использовании переменных функция Гамильтона приобретает вид: |
![]()
|
V |
![]()
|
-Щ(1 |
![]()
|
2 |
![]()
|
+ 1 |
![]()
|
В этом случае сопряженными переменными являются: |
![]() (6.Б.14)
(6.Б.14)
|
X - У *+ е -ч - Ч Л |
|
°*0»0»0»0»0»0»0* |
^•0»0»0»0»0»0»0<
,0»0«0«0»0»0.0«0
► О •
ТА - фонон
•0[9]0аала*0,0*0*°*о*о*о*о*о*о
0*°*АЛЛА*0*0*0*о*ооо*о*0‘
*0,0АЛЛЛА°*0*0*0*9999*0*0 0*0* А Л Л А *°*0*0*° 9 9 9 °*0*
•°*0А6а6аа6А0-0-0,о‘оУо9о^о-о-о
0*0ААЛЛАА°*0*0*0*999*0*0* *° А А Л А А 0*0*0*9 9 9 9*0*°
° • ° • а а л а * ° * ° * ° * о о о о о * о •
*0,0аллла0*0*0*°*9999*0*0 о. о.о666о. о.о*о*о*0*0*п*ов
°*°»аааа®*ооооо*о
•®*о.666о. о.о*о*о*оооо*о*<
•°-0А6л6А6А0-0-0,°’о-одсо-о-
0*0Аллла0,0*0*0*9999*0*0
•°-0а6аа6а0-0-0,°‘оУо9о9оУо-о-
®?°АААА^°?®*0*0*0000*0*0
5 А А А А • ° • ° * ° * ° * 9 О 0 0*0*0
°*0*АААА*0*0*°*оУодоо*о*
.0 6 6 6.0. о.
.О.00000о. о.о-о*оуоуоуо-0*0 ° * ° • X а. А А • ° * ° * о * о о о о о * о •
”^*°» а а а *0,0*0*0*С ---
>0»°аааа0*0*0*®*0 > *°ДбАбАбАб* О * О * О * о * с
°*0*АААА0*0,0*°*о‘о'о'о'
*0,0А А А А А0*0*0*0‘9 9 д <?'
•0-°46жг)ж6ж0.0-0-0-0У09090УС
Л3АЛЛА°А0*0*0‘09990’°*
,0*ААААА0*9999*0*0
0*0*0А6ААА0*0*0,°,0У0У0У0У0,0'
*0*0АаааА°*0*0*0*9990*0*0
0,0» # д д » »0,0*0*0 0 0 0*0*0*
*0*0АЛЛЛ*0*0*0*°*9999*0*0 о • ° • а а а а * ° * ° * ° * о о о о о * о •
•° • °а а а а а°* ° * ° * ®* о о о о * о * о О.0.0.6.6В6.о. о.о. о'о*оУо ово*о«
ТО - фонон
SHAPE \* MERGEFORMAT ![]()
|
, даются (6.Б.7). |
![]() Собственные моды, обладающие временной зависимостью типа е“ Для каждой моды амплитуды связаны соотношением:
Собственные моды, обладающие временной зависимостью типа е“ Для каждой моды амплитуды связаны соотношением:
|
X* |
|
К* = |
|
+ 1 |
|
031 |
|
А |
|
Л? =• |
|
-'щб |
|
1 + е |
|
0)1 |
|
(о:А |
|
ИМ |
|
V--2 |
|
|
Это позволяет нам устранить У из функции Гамильтона, но приводит к необходимости суммирования по всем модам:
|
(6.Б.19) |
Введение переменных X приводит нас к функции Гамильтона, представляющей собой сумму независимых осцилляторных функций Гамильтона, обладающих собственными частотами о)ц ±. Вместе с сопряженными переменными мы окончательно получаем:
|
|
|
|
При использовании этого уравнения в качестве исходного пункта переход к квантовой механике становится очевидным: каждый классический гармонический осциллятор становится квантово-механическим осциллятором (смотрите Дополнение 1.Г) с собственными энергиями:
|
|
(6.Б.21)
Где «число фононов» пд ± в моде либо равно нулю, либо дается целым положительным числом.
Отметим сильное подобие квантования атомных перемещений в решетке и квантования электромагнитного поля. Да и сам термин фонон отражает близкую аналогию с фотоном. В связи с этим по аналогии с фотонами мы можем говорить
О корпускулярной природе фононов. В рамках такого описания мы можем говорить об эмиссии/создании и поглощении/уничтожении фононов и т. д. Очевидно, что такое описание базируется на операторах рождения и уничтожения гармонического осциллятора (смотрите дополнение 1.Г)
Поскольку число фононов, которые могут существовать в моде п, не является ограниченным, фононная заселенность определяется той же самой статистикой заселенности, которая характеризует фотоны, что делает их бозонами. При термодинамическом равновесии (при температуре 7) среднее число фононов в моде дается таким образом соотношением:
|
|
(6.Б.22)