Оптоэлектроника

Однородное уширение

В этом случае каждая из систем, образующих ансамбль, является идентичной. Все они обладают той же самой боровской частотой колебаний и подвергаются тем же самым ме­ханизмам уширения. Для такого уширения могут быть две причины.

1А. Уширение из-за конечного времени жизни (неупругие соударения)

Особенно изящный метод, позволяющий учесть конечное время жизни заселенно­сти каждого из уровней |1) и |2), заключается в том, чтобы считать, что каждая из собственных энергий обладает мнимой частью:

Еп=Ъсо + (З. АЗя)

2*л

В этом случае вероятность нахождения частицу на уровне |п) равна:

E-iEnt/h - Q-t/in

Форма линии перехода пропорциональна амплитуде Фурье-образа волновой фун­кции, описывающей состоянии частицы |п). В этом случае функция формы линии может быть легко найдена:

А у /2к

(v-O2 +(Av/2)2

Где полуширина составляет:

(З. А.5)

1Б. Уширение из-за упругих соударений: временная когерентность

В этом случае мы рассматриваем каждую квантовую систему как подвергающуюся хаотичным толчкам, которые приводят к потере ее фазы. Таким образом, электро­магнитное поле системы т может быть представлено в виде:

(З. А.6)

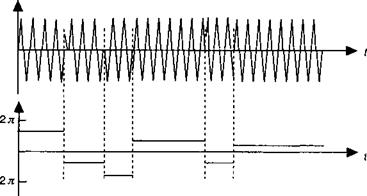
Где фт({) есть результат стохастических процессов. Рисунок З. А. 1 иллюстрирует такой про­цесс. Результирующее электрическое поле, возникающее из вклада каждой из этих иден­тичных систем, не имеющих какую-либо особую связь друг с другом, представляет собой:

E(t) = ^ Em(t) = Е^ cosffiV + <г»т(/)]

Из теории стохастических процессов известно, что частотный спектр для данных про­цессов, получаемый из оценки Фурье-образа электрического поля, есть:

(З. А.8)

Рис. З. А.1. Амплитуда и фаза электрического поля, излучаемого квантовой системой т, подвергнутой воздействию хаотичных «Пуассоновских» толчков. Сред­нее время между толчками (или же время дефазировки) есть тсо]1.

Он не имеет особого значения. Вместо этого понятия следует ввести концепцию спектра автокорреляции:

<7(бу) = |Е*({)Е(/')г ^ |£*(/)£(/ +(З. А.9)

Где мы допустили возможность того, что электрическое поле имеет комплексную компо­ненту. Таким образом, мы вводим автокорреляционную функцию первого порядка СгДт), которая дается соотношением:

7-/2 _________

С,(т)=у - ^Е*{$)Е{1 + т)& = £*(')£(' + <■) (З. А. 10а)

-Т/2

Корреляционная функция первого порядка

Эта формула применима для достаточно больших значений Г, которые обеспечи­вают сходимость статистической суммы. Существование такого предела (что мы не будем демонстрировать) является одним из основных вопросов исследования стохасти­ческих процессов, который называется эргодическим принципом. Этот принцип утверж­дает, что существует эквивалентность между статистическим и временным усреднени­ем. Знак верхней черты означает статистическое усреднение случайного процесса.

Спектр автокорреляции Щсо) и автокорреляционная функция связаны таким образом соотношением:

_ +«о

С(й>) = — Г (?, (г) стйт (ЗА 10 6)

2л 1

Таким образом, спектр автокорреляции имеет форму, близкую к форме Фуре-образа автокорреляционной функции. Для обеспечения нормировки (З. А.106) заметим, что для т - 0 уравнение (3.1 Ой) дает:

Т/2 ________

С, («)=!■ = (ЗА 11)

-7-/2

Что представляет собой среднюю интенсивность. В дополнение к этому, интегрируя (ЗА 106), мы находим, что

+оо

= | ёгС, (г)<?(г) = 6,(0) (ЗА 12)

Введем функцию формы линии g (со) как нормированный вариант (3.10.6) (т. е. без упоминания точного времени усреднения Т)

^О(со)&со

Что может быть записано с учетом (З. А. 12) и (З. А. 11) в следующем виде:

(ЗА 13а)

Форма линии и когерентность первого порядка

Где^(т) представляет собой временную когерентность излучения первого порядка:

Т/2

Еі)Е(і + г)й

Т

----------------- = §й (ЗАІЗб)

/£-«£«)<., Є'(0)

-Т/2

Уравнение (З. А.ІЗя) представляет собой основной результат статистической те­ории излучения. Форма линии спектрального распределения излучения является Фурье-образом когерентности электрического поля первого порядка[7]. Это положе­ние известно под именем теоремы Винера—Хинчина.

Нам все еще необходимо уточнить процесс, описывающий толчки частиц со средним временем между импульсами гсо11. Наиболее общим является процесс Пуассона с вероят­ностью р(т)&т того, что атом не испытает соударение в течение времени г, определяемого:

Р(т)йт = —е”,/ТсоИсіт (ЗА 14)

Гсоїі

В этом случае автокорреляционная функция поля, излучаемого т, приобретает вид:

6,(0= е'{фЛ,+т)~*Л,)) (ЗА 15)

В этом уравнении единственный ненулевой вклад обусловлен атомами, имеющими период между столкновениями, больший г, для которого фт^ + г) = 0т(О, при этом другие члены обладают нулевой средней величиной при оценке с суммированием по т, так что:

(г)= £02е~‘"”г — Те-'/г-а/ = £02е-‘"”г-г/г - (З. А.16)

В этом случае форма линии, показанная на рис. ЗА 12, дается Фурье-образом (ЗА 13а) приведенной выше автокорреляционной функции:

*(®)=7----- Ч^ТГ/---- т <ЗАЛ7>

(й)-ю21; + (1/гсоП;

Возвращаясь к выражению, полученному с использованием матрицы плотности, мы видим согласованность между формализмом матрицы плотности и статистической теори­ей света (сравните уравнения (3.43) и (ЗА 17)).

С учетом уширения из-за конечного времени жизни (3 А5) и упругих соударений (ЗА 17), однородное уширение А V в этом случае дается соотношением:

(ЗА 18)