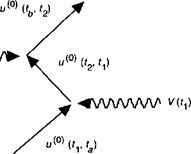
Нестационарные возмущения второго порядка
В главе 1 мы видели, каким образом нестационарный гамильтониан может обусловить переходы между различными состояниями квантовой системы. Чтобы показать это, мы записывали нестационарное уравнение Шредингера в базисе, сформированном собственными состояниями системы и анализировали член за членом все элементы дифференциального уравнения (уравнение (1.70)). Сейчас же мы представим альтернативный и более эффективный подход, обеспечивающий графическую интерпретацию временной эволюции квантовой системы в условиях внешних возмущений. Это позволит нам обобщить результаты на случай квантовых переходов более высокого порядка, таких как двухфотонное поглощение свободными носителями.
Начнем с нестационарного уравнения Шредингера, описывающего эволюцию состояния l'F(O) системы под влиянием нестационарного гамильтониана H(t):
Н(,} чЧОН^ИО) (З. Б.1)
Поскольку последнее уравнение является линейным, состояние системы в момент времени tb связано с состоянием системы в момент времени ta линейным оператором u(tb, ta), определяемым соотношением:
Этот оператор распространения должен удовлетворять уравнению:
(з. б.3)
Если гамильтониан Яне зависит от времени (#(/) = #0), то в этом случае последнее уравнение может быть легко проинтегрировано, что дает:
U(tb, ta)=e-«H°/h*>-'°) (ЗБ.4)
(в этом уравнении экспоненциальный оператор ея соответствует ЪНп/п!).
Введем базис, сформированный собственными состояниями |т) оператора #0, определяемыми Н0т) = Ejm). Используя соотношение свертки:
/ = 5>ХЧ (З. Б.5)
Т
Где / — оператор идентичности, оператор и может быть записан в виде:
При этом сот соответствует боровской частоте Ет/%.
Теперь мы предположим, что гамильтониан системы Н0 возмущен нестационарным взаимодействием V(t) так, что Н= Н0 + V(t). В этом случае оператор распространения является решением дифференциального уравнения:
|
(З. Б.7) |
![]() [#0 + v(tb)]u (ta, t„)= іh-Ј-u (tb, О а h
[#0 + v(tb)]u (ta, t„)= іh-Ј-u (tb, О а h
Беря в качестве образца для подражания замену переменных, которую мы осуществили уже ранее в (1.67), введем оператор и в соответствии с соотношением:
|
(З. Б.8) |
Иногда такую замену переменных называют картиной взаимодействия. Подставляя (З. Б.8) в (З. Б.7), получаем:
|
(З. Б.9) |
![]() І Hщh, ta)=
І Hщh, ta)=
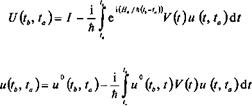
|
Или в другом виде: |
![]() Это уравнение может быть формально проинтегрировано, что дает:
Это уравнение может быть формально проинтегрировано, что дает:
(З. Б. 10)
(З. Б.11)
Уравнение Шредингера для оператора распространения
Где оператор и(0) есть оператор распространения невозмущенной системы, определяемый (З. Б.6). Уравнение (З. Б.11) не имеет практической пользы в том смысле, что это просто интегральная форма дифференциального уравнения Шрединге - ра. В то же время оно предоставляет возможность графической интерпретации и создает основу для итерационных вычислений, которые мы теперь и опишем.
Уравнение (З. Б. 11) может интерпретировано как ограниченный ряд по возмущениям возрастающего порядка, при этом м(0) соответствует первому члену этого многочлена. В этом случае оператор распространения может быть записан в виде:
|
|
(З. Б. 12)
Где:
(З. Б. 13а)
SHAPE \* MERGEFORMAT ![]()
![]()
|
Ta |
![]()
![]()
|
Ta |
![]() (З. Б. 136)
(З. Б. 136)
(З. Б. 13e)
Сейчас мы уже можем интерпретировать графически эти уравнения:
А) В первом порядке и(1): система изменяется с момента времени ta до момента времени без взаимодействия (член г/(0)(^, ^)), взаимодействует с возмущением в момент времени ^ (член К(^)) и продолжает эволюционировать без взаимодействия вплоть до конечного момента времени ^ (член и(0)(^> ^)). Рисунок З. Б.1 дает графическую интерпретацию этой эволюции, известную как Фейнмановская
Рис. З. Б.1. Фейнмановская диаграмма возмущения первого порядка.
|
|
|
|
|
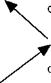
Диаграмма. Поправка первого порядка к оператору распространения в этом случае представляет собой интеграл всех этих элементарных вкладов по всем промежуточным значениям времени Для детального и более углубленного рассмотрения этого вопроса читателю рекомендуется ознакомиться с шедевром Ричарда Фейнмана: The strange Nheory of Light and Matter (1985).
Исходя из (З. Б. 136) мы можем рассчитать поправку первого порядка к состоянию системы:
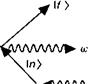
Где [) = |Ч,(0)(/ = 0)) есть начальное состояние системы, а также рассчитать скорость переходов между состояниями |/) и |/'). Затем мы могли бы возвратиться к более ранним результатам раздела 1.6, но оставляем это в качестве упражнения читателю. Теперь мы обратим наше внимание на члены разложения второго порядка. Взаимодействие второго порядка играет принципиально важную роль, когда взаимодействие первого порядка дает нулевую скорость перехода (как это имеет место в случае запрещенных переходов), б) Во втором порядке: интеграл (З. Б. 13 в) может быть интерпретирован следующим образом. Система переходит от ta к tv взаимодействует в момент времени затем переходит от /, к /2, вновь взаимодействует в момент времени /2 и переходит к tb без взаимодействия (рис. З. Б.2).
|
Со |
![]() В (З. Б. 13 в) мы заменяем выражение для невозмущенного оператора м(0) на его точное определение в соответствии с (З. Б.6), что дает:
В (З. Б. 13 в) мы заменяем выражение для невозмущенного оператора м(0) на его точное определение в соответствии с (З. Б.6), что дает:
|
R,=r r:=r,
|
|
|
|
V(t2) ЛЛЛЛЛЛД |
|
А |
![]() Рис. З. Б.2. Фейнмановская диаграмма для возмущения второго порядка.
Рис. З. Б.2. Фейнмановская диаграмма для возмущения второго порядка.
|
Поправка второго порядка к начальному состоянию |/ ) = |Ч/(0)(/ = 0)) есть |¥<2>(/)> = и<2>(/, 0)|і> или: H t,= о /,=0 / ** -- - |
|
(/N*)(*N0 , , Е-Е.-Е, П J I п і I |
|
Мы предположим, ЧТО однофотонные переходы ЯВЛЯЮТСЯ нерезонансными ((O^COj и |
|
(о/п ф (Oj), в то время как двухфотонные переходы близки к резонансу, т. е.: |
|
С/(')=^Х I Xе"" П I J п Где каждый элемент CIJn получается интегрированием (З. Б. 17) или: (<у„((Ofi-COj} __ j |
|
{/Уп)(пУ,1) і(®л, -«/) |
|
-Щ - a>j) і(®/» -®у) |
|
V(t)=Yy, |
|
Е + к. с. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
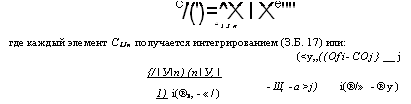 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как и в случае нестационарного возмущения первого порядка, мы узнаем, что возмущение второго порядка обусгцвливает постоянную скорость перехода <7^, которая в этом случае определяется соотношением:
|
У у у (/¥Ап)(пу1‘) |
![]()
![]()
|
4* V V Ел-Е,-Е, |
![]() Д(Ел - Ьсо1 + Нсо;) (З. Б.24)
Д(Ел - Ьсо1 + Нсо;) (З. Б.24)
Второе золотое правило Ферми
Последнее выражение называется вторым золотым правилом Ферми. Каждый член в сумме (З. Б.24) интерпретируется следующим образом: под влиянием колебаний с частотой ^система переходит из состояния |/) в состояние |п) с вероятностью перехода, пропорциональной (я|К7|/). Поскольку энергия при этом не сохраняется, переход может иметь место только в пределах временного интервала Д/, устанавливаемого вторым соотношением неопределенности (Д/= й/ДЕ или Ы(Еп. — £,)), и который проявляется как весовой коэффициент в (З. Б.24). Рисунок З. Б.Зя иллюстрирует двухфотонный процесс поглощения.
|
|||
|
|||
|
|||
|
|
||
|
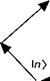
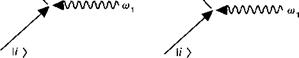
Теперь мы применим второе золотое правило Ферми к проблеме двухфотонного (2со) поглощения. Рассмотрим двухуровневую систему (|1) и |2) с межуровневым энергетическим интервалом Н со21. Эта система подвергается воздействию электромагнитной волны с частотой со. В этом случае гамильтониан возмущения имеет вид:
(З. Б.25)
![]() С учетом того, что в приведенном выражении отсутствует суммирование по индексам /и У, скорость двухфотонного поглощения, определяемая (З. Б.24), дается соотношением:
С учетом того, что в приведенном выражении отсутствует суммирование по индексам /и У, скорость двухфотонного поглощения, определяемая (З. Б.24), дается соотношением:
(З. Б.26)
![]() Поскольку промежуточными состояниями могут быть только |1) или |2), получаем:
Поскольку промежуточными состояниями могут быть только |1) или |2), получаем:
(З. Б.27)
И так как о>21 ~ 2(о:
|
|
|
|
И полагая:
(2|К|2)-(1|К|1) = ^И (З. Б.29)
(2|г|2)-(1|ф) = $2
Находим, что скорость перехода между двумя состояниями системы составляет:
= *И*(Е^'Л 6{р>'= 2(о) (3-Б-30)
8Ь (со21 - со)
Таким образом, даже если переход |1> —> |2> не разрешен в первом порядке, двухфотонный переход разрешен до тех пор, пока элемент 6п не равен нулю (т. е. до тех пор, пока система асимметрична). Осциллирующая волна с частотой со испытывает ослабление интенсивности (= есЕ2/2пор) во время распространения, равное:
-?-1ш = 2Нс>С„(М1-М1) (З. Б.Э1)
О1
Где и Ы2 соответствуют плотности заселенности своих соответствующих уровней. Подставляя (З. Б.ЗО) в (З. Б.31), мы видим, что поглощение может быть записано в виде:
^-К = - РЧ (З. Б.32)
01
Где Р представляет собой коэффициент двухфотонного поглощения, определяемый соотношением:
|
(З. Б.ЗЗ) |
Е с Тг (со,, - со У
Коэффициент двухфотонного поглощения
Эта теория без труда может быть обобщена для трактовки двухфотонных переходов в полупроводниках. В этом случае (З. Б.ЗЗ) должно быть проинтегрировано по всей зонной структуре с использованием процедуры, изложенной в другом контексте в главе 5. В таблице З. Б.1 представлены коэффициенты двухфотонного поглощения в различных материалах. Двухфотонное поглощение имеет очень важное значение, так как оно ограничивает плотность оптической мощности излучения, которое может распространяться в оптоэлектронных компонентах (например в лазерах, модуляторах и т. д.). Двухфотонное поглощение может использоваться также и для оптической защиты от избыточных лазерных пучков.
|
Табл. 3.1. Коэффициенты двухфотонного поглощения для различных полупроводниковых материалов. Показанный разброс по величине /? обусловлен большими экспериментальными трудностями, связанными с измерением этого параметра
|
![]()
|
З. В. Коэффициенты Эйнштейна для двух предельных случаев |
![]() Пример
Пример
А) Рассмотрим лазер на основе ваАз с волноводным слоем с толщиной 0,1 мкм и с шириной 5 мкм. При внутренней мощности излучения 500 мВт плотность мощности /0 излучения составляет 107 Вт см-2, что приводит к двухфотонному поглощению /?/0 (/?= 25 см ГВт“1) или к паразитным потерям амплитудой 0,25 см-1. Это не является пренебрежимо малой величиной, при этом двухфотонное поглощение ограничивает уровни мощности излучения, которое может легко распространяться в волноводах на основе ваАБ.
Б) Брусок 1пБЬ толщиной 1 мм помещен перед фокальной точкой линзы, что обеспечивает диаметр световой точки 0,5 мм или площадь освещенной поверхности 2 х 10-3 см2. Мощность выходного излучения на выходе бруска дается в этом случае интегралом дифференциального уравнения (З. Б.Э2):
|
|
(З. Б.34)
Где /0 — мощность излучения на входе. При мощности 2 МВт (или плотности мощности 1 х 109 Вт см-2) плотность мощности на выходе равна Я/d или 1/(5 х 103 см ГВт-1 х х 10"1 см), что равно 2 х 10_3 ГВт см~2. Это соответствует коэффициенту ослабления 7//0 = 2 х 10~3.