Оптоэлектроника

Насыщение усиления и /С-фактор

В главе 14 (уравнение (4.10)) мы видели, что усиление в газовых или ионных лазе­рах является насыщаемым, т. е. усиление в функции плотности фотонов 5 в резона­торе может быть записано в виде ^(я) = У^/( + где У0 есть усиление холодного

Резонатора (см-1). Это насыщение приводит к стабилизации лазерного усиления до его стационарного значения (смотрите рис. 4.6). В предположении, что потери у порога Ас (= 1 /с? тс) равны приведенному выше уравнению для ^(я) можно получить плотность фотонов в функции тока накачки. Указанное насыщение имеет место вследствие конкуренции между скоростью накачки Я и двумя участвующими меха­низмами обеднения возбужденного уровня, а именно: стимулированной эмиссией и рекомбинацией носителей (излучательной или безызлучательной). Тот же самый эффект имеет место в полупроводниковых лазерах, в которых эти два последние механизма включают в себя межзонные переходы (смотрите рис. 13.Е.1). Мы легко находим, что плотность насыщения фотонов составляет $ Ыег = 1А^, 1п1ег> где ^ есть скорость света в материале, § — дифференциальное усиление и T( Ыег = — время

Жизни внутризонной рекомбинации (смотрите уравнение (13.69)). Сравнивая это

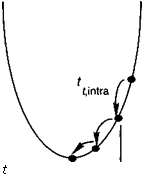
Рис. 13.Е.1. Межзонный и внутризонный ме­ханизмы релаксации, приводящие к временам релаксации /Г. п1ег и 1п1га: СВ-зона проводимос -

ти, VB-валентная зона.

VB

Выражение с (4.9), мы видим подобие того, какую роль играет дифференциальное сечение g в полупроводниковых лазерах и оптическое поперечное сечение стор в атомных лазерах.

Это межзонное насыщение является насыщением только с точки зрения мощно­сти в оптических усилителях (как, например, в МОРА). Однако, в лазерных диодах выходная мощность в рамках этого подхода остается линейной функцией тока на­качки. Принимая типичные значения с' = 1010 см с-1, # = 10-15 см2 и /Ыег = 1 не, мы получаем плотность внутризонного насыщения на уровне 1014 см-3. Имеется еще и другой механизм насыщения, связанный с внутризонной релаксацией (смотрите главу

6 и рисунок 13.Е.1). Характеристические времена релаксации составляют величину порядка пикосекунд (£п1га = 1 пс). С использованием выражения 5 ,п1га = 1 /с'^ Ыга это приводит к плотности внутризонного насыщения порядка 5 Ыга = 1017 см-3. Этот последний тип насыщения может рассматриваться в динамических уравнениях по­лупроводниковых лазеров как мгновенный и он дается другим выражением:

(13.Е.1я)

Или:

Y(N,S)= Y(N)(L-Ss)

Здесь £ есть коэффициент подавления усиления и он составляет величину порядка нескольких 1017 см-3. Таким образом, плотность фотонов всегда мала по сравнению с 1/е. В связи с этим мы будем использовать вторую формулу (13.Е.1 б) так она приводит к более простым результатам.

Для включения этого нового эффекта в описание функционирования лазера вновь возвратимся к (13.69) и включим в эту формулу выражение для насыщенного усиления (13.Е.1 б) т. е.:

(13.E.2)

— = [Г G (n, s)- yc]s

Dt

Здесь: G(n, s) = с'у(п, s) есть скорость эмиссии (с-1) тогда, как ус = 1 /г и yiot = 1 /tiox есть соответственно скорость резонаторных потерь и скорость безызлучатель - ной рекомбинации. Для иллюстрации влияния члена насыщения е на стацио­

Нарные характеристики лазера выберем модель для усиления лазерной среды в виде У(п) = G(n — л1г), где, как мы напоминаем, П1т есть концентрация в режиме прозрачности.

В стационарном состоянии число фотонов 50 определяется нетривиальным ре­шением системы уравнений (13.Е.2), полученным с учетом сЫ/ск = (15/(1/ =0 для

— = — + C'G("O ~ ) (1 - «о >о

Qd ttni

Гc'g(n0 -«„)(• - *»о)= — гг

Устраняя п0 из обоих уравнений, мы получаем уравнение второй степени:

- '-Ј-(j - J )

J V J threshold )

Ttotcg 1 - es0 qd Здесь мы использовали для /threshold выражение:

/ - AtL - SL

Threshold — . ^/threshold . «tr ' - p /

*tot *tot * С с J

В том случае, когда e мало, мы вновь возвращаемся к ситуации, описанной в

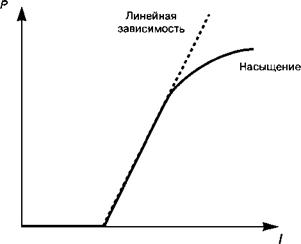
(13.72) , т. е. к линейной зависимости s от плотности тока J, как только / превысит threshold - Когда плотность тока J становится большой настолько, что более нельзя пренебрегать es0 по сравнению с 1, зависимость плотности фотонов sQ становится сублинейной, как это и следует из (легко получаемого) решения уравнения второй степени (13.Е.4). Рисунок 13.Е.2 иллюстрирует результирующую зависимость мощ­ности излучения от тока накачки.

Динамические характеристики лазера могут быть получены из записи п = п0 + 8п, J= JQ + SJh s = s0 + Ss, где изменения параметров а (п, Jили s) являются гармоничес­кими функциями вида ~SaЂuot. Рекомбинационный член G(n, s) = cfg^n — ntr)( 1 — es) может быть представлен в виде разложения:

Здесь члены разложения определяются формулой:

= с'*0; = -£с')о

Таким образом, мы проводим разложение (13.Е.2), удерживая лишь члены пер­вого порядка и используя условия равновесия (13.Е. З), которые могут быть записа­ны здесь в виде С<70 = ус и Цдс1 = умп0 + 6«^,, что дает:

Ц - = 6п(ш + Г„)+ &(б>0 + б») Да

БпТЄ^0 = &(ій>- Г<7550) = б(ісо+ Г5)

В это выражение мы ввели члены затухания:

= 7юі ■*" = ^с? о**о (13.Е.8)

Здесь Гп есть коэффициент затухания, уже полученный в разделе 13.7 (уравнение (13.7Б)), который описывает потери в системе (а именно, утечку фотонов из резо­натора и безызлучательную рекомбинацию носителей). Г5 представляет собой но­вый член, связанный с насыщением. Система уравнений (13.Е.7) может быть про­сто решена подобно (13.75), что приводит к динамической характеристике лазерно­го диода:

Г / Дс!

(13.Е.9)

(о) + Г„)(іа + Г,)+ Г<7„<7050 Здесь мы пренебрегли <7 по сравнению с <70. С учетом того, что нас интересует только амплитудная характеристика лазерного диода, (13.Е.9) может быть пред­ставлено в виде:

В это выражение мы ввели следующие параметры:

• (угловую) частоту релаксации а)я, определяемую:

(13.Е.12) (13.Е.13)

Этот коэффициент мы выражаем как функцию резонансной частоты / в виде:

(13.Е.14)

В это выражение входит коэффициент К, представляющий собой временной (в общем случае) параметр, выражаемый в не и определяемый выражением:

(13.Е.15)

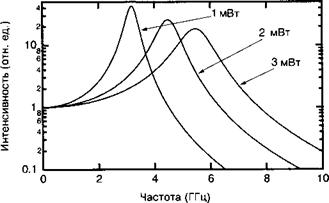
Выражения (13.Е.11)—(13.Е.15) показывают, что кривые резонансной релакса­ции уширяются пропорционально параметру Гл, который, в свою очередь, возрас­

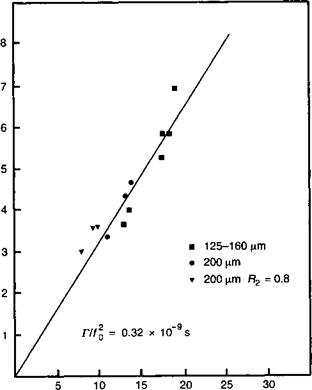
Тает более быстро с внутренней плотностью фотонов 50 (т. е. с внутренней мощно­стью) по сравнению с тем, как это предсказывается простой теорией раздела 13.7 (смотрите рис. 13.Е. Э). Экспериментальный график «ширины резонанса ГЛ в функ­ции резонансной частоты /Л' позволяет определить время жизни носителей и коэффициент подавления усиления е. Экспериментальные данные, приведенные на рис. 13.Е.4 ясно показывают, что на коэффициент к доминирующее влияние оказывает эффект насыщения усиления. В предположении, что типичная величина е составляет 5 х 10"17 см3, e|dg{s равняется 5 х 10-17 см3/(3 х 10"16 см2 х 9 х 109 см с-1) или 18 пс, что явно преобладает над резонаторным временем жизни г (порядка 1—2 пс) в выражении для коэффициента К (13.Е.15).

Продолжение табл. 13.Е.1