Механизмы рассеяния
Механизмы рассеяния абсолютно необходимы для правильного описании электрических свойств материалов. Более того, эти процессы объясняют пропорциональность между индуцированным током и величиной приложенного электрического поля (закон Ома). Среди этих механизмов наиболее важные вклады даются рассеянием носителей заряженными примесями и фононами. Фононы (колебания решетки) и элект - рон-фононное взаимодействие будут рассмотрены в дополнениях в конце этой главы. Здесь же мы рассмотрим рассеяние носителей на примесях, процесс, в котором доминируют остаточные ионы, используемые при легировании основного полупроводникового материала.
С учетом длины волны электронов в зоне проводимости заряженную примесь можно рассматривать как точечный заряд Ze. Поскольку этот заряд располагается в кристалле, содержащем свободные электроны, мы можем ожидать, что концентрация электронов вблизи примесей увеличивается, приводя к значительной экранировке электрического поля дефекта. Наиболее простая возможная (и тем не менее очень эффективная) трактовка этого явления, описываемая далее, приписывается Дебаю. Мы знаем, что в невырожденном полупроводнике зона проводимости характеризуется средней электронной плотностью п0 = УУехр(—(Ес — Е^/квТ) (смотрите
(5.42) и (5.43). Если мы добавим медленно изменяющийся (по сравнению с постоянной решетки) электростатический потенциал К(г), каждый электрон будет обладать в дополнение к своей решеточной энергии £(к) еще и потенциальной энергией — еУ(т) (смотрите рис. 6.4). В этом случае мы можем отобразить полную зону проводимости как будто смещенную вертикально на энергию — еУ (г). При термодинамическом равновесии энергия Ферми постоянна в пределах всей системы, при этом концентрация электронов изменяется в соответствии с соотношением:
|
ЕУ( г) |
![]() І А! ІX - еУ(г) - ЕЛ
І А! ІX - еУ(г) - ЕЛ
|
(6.24 а) |
![]() П(г) = Nc ехр<| - ^ = п0 ехр
П(г) = Nc ехр<| - ^ = п0 ехр
КвТ
В этом случае изменение, обусловленное потенциалом, составляет:
ЕУ( г)
|
Ры(г) = ~е(" ~ по) = - еп0ехр |
![]() ^ = - еЯ20У{т) (6.24б)
^ = - еЯ20У{т) (6.24б)
|
К. Т |
![]() К оТ
К оТ
Где линеаризация заряда определяется дебаевским волновым вектором ^ или дебаев - ской длиной Л0= /я0ъ соответствии с соотношением:
ЕкгТ
|
_ еквТ |
![]() (6.25) Т
(6.25) Т
Дебаевские волновой вектор и длина
|
А |
![]()
|
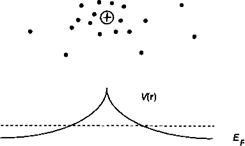
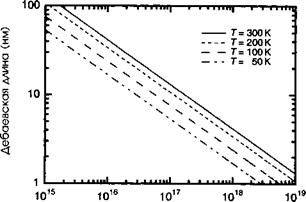
Рис. 6.4. Электроны проводимости аккумулируются вблизи положительно заряженной примеси, таким образом экранируя примесный потенциал на длине, характеризуемой длиной волны Дебая (а). Дебаевская длина экранировки в функции уровня легирования (б) для ваАБ (ек = 12) при различных температурах. |
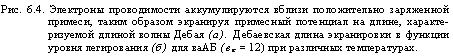
|
,6 Концентрация электронов (см-1) |
![]() Этот параметр важен, так как он описывает характерную длину в пределах которой электронный газ может экранировать внешний потенциал. Этот момент лучше иллюстрируется при рассмотрении электростатического потенциала из-за плотности наведенного заряда /?ех1(г). В этом случае такой потенциал определяется уравнением Пуассона:
Этот параметр важен, так как он описывает характерную длину в пределах которой электронный газ может экранировать внешний потенциал. Этот момент лучше иллюстрируется при рассмотрении электростатического потенциала из-за плотности наведенного заряда /?ех1(г). В этом случае такой потенциал определяется уравнением Пуассона:
У2К = = - Ра* + РтЛ = -&2- + а1У (6.26)
Е е е
Где е есть проницаемость среды (е= ея£0). Этот уравнение может быть решено с использованием Фурье-преобразования:
У(ь — РехДк) _ ^ехДк)
[кг +я1)е 1 + (я1/ к2)
Для точечного заряда р(г) = 2е8(г), такого, что Дк) = находим (после отчасти длинного обратного преобразования) полный и внешний потенциалы:
|
|
7 ~Ч°Т 7
К(г) = ^£-£_, |/м(г) = -^- (6.28)
4 ЯЕ Г 4л£Г
Что, естественно, дает экранированный кулоновский потенциал на расстоянии порядка дебаевской длины.
Пример---------------------------------------------------------------------------------------------------------------------------------------------------
Для ваАБ, легированного до уровня 1017 см-3, находим:
|
НМ |
![]() , _ е(квТ/е) _ 112х8,8хЮ"'2 х0,026 _ ° еп0 1,6х 10_19 х 1023
, _ е(квТ/е) _ 112х8,8хЮ"'2 х0,026 _ ° еп0 1,6х 10_19 х 1023
Рассчитаем теперь вероятность рассеяния электрона, изначально находящегося в кристалле в состоянии к и обладающего волновой функцией:
^к(г) = ~^ик(г)е'кг (6.29)
Распределение рассеивающих примесей, расположенных при г., дается выражением:
У
Возвращаясь к стационарной теории возмущений, рассмотренной в разделе 1.6.2, с учетом стационарного потенциала, вводимого в момент времени I = 0, и с использованием золотого правила Ферми находим вероятность скорости перехода в состояние к':
5(к к') = ^(к'^к^^к') - £(к)] (6.31)
Что с точностью до множителя представляет собой ту же самую формулу, которая дается уравнениями (1.78) и (1.83) для (о = 0. В данном случае множитель в четыре раза больше, так как мы не выделили временную зависимость для положительных и отрицательных частот. Закон сохранения энергии показывает, что такие столкновения являются упругими (смотрите рис. 6.5).
Подставляя волновые функции для состояний к и к7, находим выражение для матричного элемента:
(к1|/»1к>^1“;<гК<г|е"‘",'>'''<г)<1‘г■ -^ТкГГкрТДТ?6""1""-' <6'32>
Где в дополнение к периодичности волновых функций ик мы использовали следующие аппроксимации:
• К^Дг) существенно не изменяется в пределах периода кристалла;
•  Интеграл перекрытия составляет:
Интеграл перекрытия составляет:
©
|
Б |
![]()
|
А |
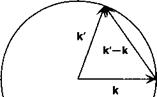
![]() Рис. 6.5. Столкновение электрона с примесью в реальном (а) и обратном (б) пространстве.
Рис. 6.5. Столкновение электрона с примесью в реальном (а) и обратном (б) пространстве.
|
/(к', к) = Гик*(г)ик(г) |
|
|
2п |/(к', к)|: |
|
2 4 Z г |
|
1 |
|
5(к -> к') = пт |
|
ЯЕ(Ю-Е(Ъ)] |
|
|
|
|
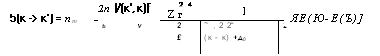 |
|
|
|
|
|
|
||
|
|||
|
|||
|
|||
|
■(*) |
|
При этом интеграл может быть рассчитан с использованием сферических координат (к, в, ф) и соотношения 8((?12/2т*)(к'2 - к2)) = (т*/1г2к)8(к/ — к): |
|
?_ Г Уй3 к' (1 - соб в > [е (А: ’)- Е (к )] Уе У 2 £ (1 _ С08 0 ) + д2в |
|
2 к Z е ~Ь |
|
|
|
|
|
|
|
|
|
2к_ Чо |
|
1п |
|
1 + |
|
||
|
||
|
||
|
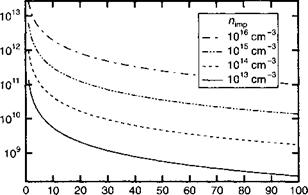
Мы можем убедиться, что скорость переходов по порядку величины составляет 0(к), если к « и составляет величину порядка 0(кЧп(к)), если к » Рисунок 6.6 демонстрирует численную величину 1/гдля различных значений п. тр при комнатной температуре для ваА*. Представленные на рис. 6.7 значения подвижности получены численной оценкой интеграла в (6.16). |
|
|
|
О О А |
|
О О А О * О |
|
Энергия (МэВ) Рис. 6.6. Величина 1 /т(£) для рассеяния на заряженных примесях при Т= 300 К в ваАБ |
|
|
|
О со |
|
2 О |
|
О 0 0 * з: Со < О С= |
|
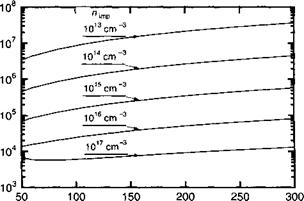
Температура (К) Рис. 6.7. Подвижность, определяемая рассеянием на заряженных примесях. |
В действительности, как мы увидим, что при комнатной температуре рассеяние на фононах доминирует над примесным рассеянием во всех случаях за исключением образцов, обладающих примесной концентрацией выше п. тр = 1017 см-3.