Метод Кейна
Модели почти свободных электронов и жесткой связи очень полезны в дидактических целях, но одновременно они обладают существенным недостатком. На практике чрезвычайно трудно, отправляясь от экспериментально определяемых параметров (например, кристаллическая структура, электронная структура образующих материал атомов, ...), предсказать, какова будет ширина запрещенной зоны, например, в GaAs и т. д. Эта трудность возникает из-за сильно упрощенной природы аппроксимаций, использованных при получении результатов дополнений 5.А и 5.Б. Введение малейших усложнений приводит к необходимости чрезвычайно трудных вычислений. Рассматриваемый к • р-метод представляет собой полуэмпирический подход, использованный Кейном при расчете зонной структуры и использующий экспериментально доступные данные (полученные из оптических измерений и т. д.)
2
|
(5 В.1) |
![]() Я^(г>= Т^+,/<г> ¥.л{г)=Е^¥,л(г),
Я^(г>= Т^+,/<г> ¥.л{г)=Е^¥,л(г),
Где (// k есть блоховские функции:
|
(5.В.2) |
![]() К kW = “п, k(r)e, kr
К kW = “п, k(r)e, kr
Мы видим, что оператор р = — действует на волновые функции Блоха - Фуке следующим образом:
|
|
|
Р2 П2к2 Ь. ч +---------- + —к р + ^(г) 2т 2т т |
|
Ч,.к(г) = Е„ЛипЛ(г) |
|
Р~ Ь2к2 Ь. ч + —----- + — к р + У(г) |
|
(к)и„,0(г) = ^Еіп)(к)сГ(кК„о(г) (5.В.7) |
|
.(») |
|
2т0 2т,, та |
|
Ь2к - л 2тп |
|
(5.В.8) |
|
Это уравнение представляет обычную проблему диагонализации матрицы эффективного гамильтониана. Если все элементы (им 0|р|ит 0) известны, мы можем непосредственно диагонализировать матрицу. Однако, это не всегда возможно. К тому же действительный интерес представляют только области зон вблизи запрещенной зоны. Для к вблизи 0 члены, обусловленные оператором к • р, можно рассматривать как возмущения. Если мы определим: |
|
- к • (им о |р| ит |
|
Н кр = 11 Мт |
|
Т, |
|
СГ(Ю+ £//&^>(к) + £ Я&с^к) = 0 (5.В.11) |
|
Е{"К) |
|
Для пе МхиМе М2 последняя сумма намного меньше первой. Это дает: Н кр г {п) (к^ П МтСт |
|
Г. (») " М |
|
, М є М2 |
|
Е(П)Ф)-ЕМ „ |
|
При пе МхиМе Мх мы подставляем этот результат и находим: £(л)(к) |
|
1 1 2к2 |
|
Ем. о + |
|
2 т, |
|
Т'е М. те М, |
|
Те А/, |
|
•Г(к) + ^Я1сГ(к) = 0 |
|
■~Е{п)( к) |
|
2т, |
|
+ Г(г) |
|
М„ 0(г) = Еп 0и„ 0(г) |
|
2т |
|
||
|
||
|
||
|
||
|
||
|
||
|
||
 |
||
|
||
|
||
|
||
|
||
|
||
 |
||
|
||
|
Ь2к2 2 тп |
|
- Е{пк) |
|
Ем о + |
|
|
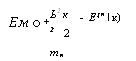 |
|
|
|
|
|
|
? Н»т. нхя 0)- Ет. |
|
Н кр' = 11 Мт |
|
|
|
||
|
|
||
|
|||
|
(5.В.16) Г/0 "‘0 ”’*с 0 _ ^ пи 0 Естественно, что самый важный вклад обусловлен состояниями, ближайшими по энергии — состояниями валентной зоны. Если мы пренебрежем другими членами суммы, то навдем: |
|
-|("с. о|л|"* 0)Г |
|
Ь2 к 2 Ь 2 к 2 Еи)( к) = Ес0+^^ + ^— |
|
2/Ил |
|
Ь2к2 Ь2к2 Р2 |
|
£(°(к) = Ес 0 + |
|
2то Е8 |
|
2 тп |
|
Р2 |
|
1 + |
|
М«.о) |
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В зоне проводимости. Это предсказание экспериментально подтверждается, и тот факт, что /яс//я0 «1 обусловлен сильной связью Р2/Е8 »1 между зоной проводимости и валентной зоной.
|
1-^1 |
![]() Тот же самый метод легко применить и к валентной зоне (которая предполагается невырожденной), при этом в данном случае мы получаем:
Тот же самый метод легко применить и к валентной зоне (которая предполагается невырожденной), при этом в данном случае мы получаем:
(5.В.20)
Тп
Е
Это свидетельствует о том, что эффективная масса дырок должна быть приблизительно равной эффективной массе электронов. К сожалению, ситуация с валентной зоной более сложная, поскольку эта зона вырождена в максимуме.
К сожалению, мы не можем приводить детальные расчеты для валентной зоны, поэтому мы ограничимся качественным описанием результатов.
Кристаллический потенциал К(г) обладает симметрией структуры цинковой обманки. Это означает, что его величина является неизменной при применении операций симметрии по г. С учетом аспектов симметрии можно показать, что такой потенциал приводит к трехкратно вырожденным собственным состояниям в центре зоны Бриллюэна, при этом вырождение не зависит от амплитуды потенциала. Валентная зона как раз и обусловлена такими состояниями.
Три базисные функции могут быть обозначены как |Х), |У), Т), где буквы обозначают свойства симметрии этих волновых функций. Результат действия операций симметрии на любую из этих функций сводится к их отражению в базисе двух других (или обратно самой на себя). Возьмем, например, зеркальное отражение в плоскости (111) (смотрите рис. 5.1), что соответствует изменению координат х -> у, у -> х, I -> I - Базисные функции обладают свойствами:
Х) = их(у, х, г)=иг(х, у, г)
У) = иу{у, х, г)=иЛ(х, у, г) (5.В.21)
Скажем, что эти функции преобразуются между сЪбой как х, у и z С учетом таких свойств симметрии легко показать, что оператор импульса р = Н / IV дает нулевой матричный элемент по этим двум функциям. Возьмем, например, )•
Вращение на к вокруг оси I преобразует ^) в 7), рг в рг и 1^) в — Х). Таким образом, {2 р^Х) = —&ргХ) = 0. Снятие вырождения при к ф 0 за счет к • р взаимодействия не может произойти из-за связи между другими функциями валентной зоны, но в обязательном порядке происходит из-за взаимодействия с другими зонами. С учетом ограниченного базиса, сформированного тремя функциями валентной зоны, кубическая симметрия приводит (смотрите (5.В. 14)) к эффективному взаимодействию в виде:
|
</ |к • Р|У ) |
Х) |
1 Г) |
г) |
|
<* |
Ьк] +М{Ц+к1) |
Мхку |
ЩК |
|
(Г |
Мкукх |
Ьк) + М(к +к2х ) |
Шу кг (5.В.22) |
|
<7 |
Мккх |
Мкку |
Ьк* + М (кх2 +ку2) |
С тремя различными константами Ь, М, N. Теперь мы уже можем диагонализиро - вать эффективный гамильтониан с тем, чтобы получить вид трех валентных подзон для к ф 0 и с учетом этих трех параметров. К сожалению, наши трудности на этом не кончаются, так мы должны все еще учесть спиновое и спин-орбитальное взаимодействие. Если не учитывать последний вид взаимодействия, то влияние спина
Привело бы к удвоению числа возможных состояний в каждой валентной подзоне с полным вырождением 3x2 при к = 0.
Спин-орбитальное взаимодействие обусловлено релятивистским эффектом, который качественно может быть объяснен следующим образом: электрон пересекает электростатический потенциал на огромной скорости. В системе отсчета электрона электрическое поле, связанное с этим потенциалом, преобразуется в магнитную компоненту, которая, в свою очередь, взаимодействует со спином электрона. В результате этого движение электрона и его спин оказываются связанными. Это приводит к тому, что оператор спина более не коммутирует с гамильтонианом. При этом изначально 3x2 — вырожденные уровни расщепляются на два уровня, один из которых четырехкратно вырожден, в то время как второй вырожден двукратно и располагается на Д0 ниже первого уровня. Снятие этого вырождения происходит в полной аналогии с орбиталями рх, ру, р1 в атоме под влиянием спин-орбитального взаимодействия. В результате этого угловой момент / = 1 и спин 5 =1/2 более не являются хорошими квантовыми числами. С другой стороны, новыми стационарными состояниями системы являются собственные векторы наблюдаемых /2 и У , где 3 = Ь + 8. Наблюдаемая /2 имеет собственные значения /2 =у(у + 1) су = 3/2 и 1/2. Состояние у = 3/2 является четырежды вырожденным с 11 = ±3/2, 11 = ±1/2, а состояние 11 = 1/2 является дважды вырожденным с = ±1/2. Новые стационарные состояния являются теперь линейными комбинациями базисных функций ХТ), Х1), |УТ), У1), |гТ>, ^1), а новые состояния обозначаются как [/, уг>, что является общепринятым в атомной физике. Это усложняет вид к • р-матрицы с малой компенсацией, как можно заметить, вблизи к = 0 мы можем ограничиться уровнем у = 3/2, применяя метод Левдина к возникающим матрицам формата 4 х 4. Тот факт, что здесь имеется всего три параметра, обусловлен влиянием кубической симметрии. Достаточно кропотливые расчеты приводят нас к следующему виду эффективного гамильтониана в базисе |3/2, ±3/2) и |3/2, ±1/2):
|
|
|
|
|
|
|
![]()
![]()
![]()
![]()
![]()
С элементами:
Н„ =-^— (г, + ГгХк? +к^)-^—(г1-2у2)к^
2/я„ 2т0
+к})--^—(у1+2у2)1с?
2т0
|
2 тй
|
|
|
Где три параметра Латтинджера уг у2, у3 связаны с параметрами Ь, М, и соотношениями ух — 2т0(Ь + 2М)/3, у2 = 2т0(Ь — М)/ 6, у3 = 2т0М/в. Эти параметры для СаАБ и 1пР приведены в таблице 5.В.1.
|
Табл 5.В.1. Значения различных параметров Кейна—Кона—Латтинджера, используемые при расчете зоной структуры ваАБ и 1пР
|
Диагонализация эффективного гамильтониана (5.В. 14) приводит к дважды вырожденным энергиям:
|
{н„-нЗ 4 |
|
+ ь2 |
|
||
|
||
|
П2 2щ |
|
= Е + |
|
(1 - Г, У - ±^у;к> +2{у: - у;]к;к; + к;к; + к2к; ) |
|
|
Если мы введем вклад свободных электронов в константу уг мы увидим, что знак ± перед квадратным корнем соответствует массе тяжелой дырки (+) и легкой дырки (—). В любом из этих двух случаев имеется зависимость от направления к. В направлении (100) и эквивалентных направлений мы имеем:
|
(5.В.26) |
А в направлении (111):
|
(5.В.27) |
![]() = -71+ 2Гз> — = - Г, ~ 2/:
= -71+ 2Гз> — = - Г, ~ 2/:
Из этого мы можем заключить, что эквипотенциальные поверхности являются сферическими только, если у2 = Уу
Наконец, нам необходимо экспериментально определить параметры Латтинджера для данного полупроводника. На практике измерения с использованием циклотронного резонанса используются для определения формы дырочных эквипотенциальных поверхностей, по которым методом наилучшего подбора варьируемых параметров (5.В25) до наилучшего совпадения с экспериментальными зависимостями и определяются параметры Латтинджера.
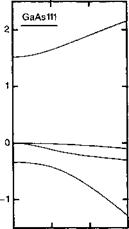
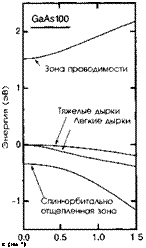
Рисунок 5. В. 1 иллюстрирует зонную структуру СаАБ, рассчитанную к • р-методом с учетом 9x2 зон в (5. В. 10).
Вблизи к = 0 мы видим, что зависимость от к для зон тяжелых и легких дырок близка к (5.В.25), но по мере того, как мы перемещаемся от центра зоны Бриллю - эна, тем менее аппроксимация эффективной массы становится справедливой.
|
|
|
Рис. 5.В.1. Зонная структура GaAs, рассчитанная с использованием к • p-метода и с учетом 9x2 зон в (5.В. 10). Вблизи к = 0 зоны тяжелых и легких дырок изменяются в соответствии с (5.В.25). Однако по мере удаления от центра зоны аппроксимация эффективной массы становится все более неудовлетворительной. |
|
А О |
![]()
|
О |
![]()
|
00 05 1.0 1.5 К (нм ’) |
![]()
|
К (нм ’) |
![]()
SHAPE \* MERGEFORMAT ![]()