Оптоэлектроника

Линейная оптическая восприимчивость: поглощение и оптическое усиление

Материя состоит из отрицательно заряженных частиц (электронов), которые экра­нируют фон положительно заряженных ядер. Когда электромагнитная (ЭМ) волна воздействует на материю, движение электронов (легких частиц) относительно ядер (тяжелые частицы) вызывает эффект осциллирующего диполя, который излучает синхронно с полем. Это и есть атомная поляризация. Излучаемое поле взаимодей­ствует с первичным приложенным полем, что и приводит к уменьшению скорости света в среде. Этот эффект может быть учтен с использованием микроскопического

Подхода, основанного на использовании выражения для осциллирующего диполя (уравнение (2.А.18)). Рекомендуем читателю углубить свои знания по этому поучи­тельному аспекту преломления, прочитав легендарные Фейнмановские лекции.

В то же время, будучи менее проясняющими, уравнения Максвелла предоставля­ют намного более эффективный инструментарий для учета этого эффекта без необхо­димости прибегать к сложным выражениям. С этой целью в уравнение Фарадея - Ампера вводится ток смещения из-за движения связанных зарядов. Это приводит к уравнениям Максвелла для незаряженной, немагнитной и поляризуемой среды:

УхЕ(г,0 = ~В(г,0

(3.29)

(3.30)

И — вектор поляризации системы вблизи резонанса, а Р — вектор поляризации, соот­ветствующий всем нерезонансным вкладам (т. е. вкладам, возникающим из-за ма­териала среды, в которую помещена двухуровневая система). Член є0Е - I - Р являет­ся, по определению, диэлектрической константой, заменяемой на гЕ. Подобным же образом, следуя определению линейной оптической восприимчивости (3.24б), выражение (3.30) может быть переписано в виде:

(3.31)

В качестве решений уравнения Максвелла (3.28) и (3.29) допускают бегущие волны вида:

Е(г, /) = Е0Яе[е-^г-^]

Где на этот раз волновой вектор к и радиальная частота со связаны соотношением:

(3.33)

Где пор — коэффициент оптического преломления равный /е0 . Так как восприимчи­вость может и не быть большой величиной по сравнению с единицей, то:

Действительная часть последнего выражения свидетельствует о том, что скорость света уменьшается на коэффициент в среде. И вновь читателю рекомендуется углубить свои пред­ставления по этому аспеюу, читая Фейнмановские лекции. Подставляя (3.34) в (3.32), мы ви­дим, что амплитуда электромагнитной волны экспоненциально ослабляется с расстоянием:

(3.35)

Где кк дается действительной частью (3.34), а коэффициент а представляет собой коэффициент поглощения, определяемый как:

(3.36)

Коэффициент поглощения и линейная восприимчивость

Или:

(3.37)

Коэффициент поглощения в двухуровневой системе

Электромагнитная волна теряет свою интенсивность в функции расстояния распро­странения как /(г)= /0е_аг, при этом ее энергия превращается в тепло. Представляется принципиальным отметить, что фазовая задержка члена %ы на 90° по отношению к распространяющейся электромагнитной волне в качестве основной причины обус­ловлена именно тепловой диссипацией энергии (и необратимостью этого процесса). Это является общим результатом, приложимым ко всем линейным процессам.

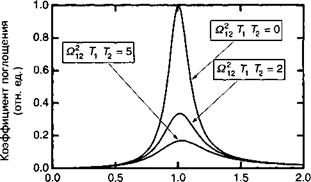
Рисунок 3.1 иллюстрирует изменение формы нормированной частотной зави­симости коэффициента поглощения для различных значений произведения 0?12 Т{Т2. Численные константы в (3.37) были выбраны таким образом, чтобы а(со21) = 1 для О, п = 0. Отметим, что поглощение уменьшается по мере возрастания интенсив­ности электромагнитной волны, при этом ширина пика возрастает как:

(3.38)

Ния £12п Тх Т2.

Это явление называется насыщением поглощения, и мы возвратимся к нему поз­же в главе 4. При малой интенсивности волны — Ы2 = уравнение (3.37) прини­мает вид лоренциана, который сможет быть получен в рамках классической теории упруго связанного электрона:

А(а)*>Ы, д Л /п]а>-(ои)= /21асЫ(со) 1£§тсп0р

Где Цсо) — лоренциан с шириной 1/Г2 и центром в 0:

Форма лоренциана

Где АV — полуширина (Р¥НМ) лоренциана (Ау = 1/Т2 =2Г2). асЫ есть результат классической теории Лоренца, а/^ — безразмерная физическая величина, называ­емая силой осциллятора, которая описывает интенсивность квантового взаимодей­ствия между двумя уровнями |1) и |2):

Л. =^-Еп(1г е2)( (3.40а)

Сила осциллятора для перехода |1)-> |2)

Для системы с несколькими уровнями мы можем показать справедливость пра­вила Томаса—Райха—Куна (Дополнение З. Г):

2/=1 <140<5)

/•*/

Это правило утверждает, что хотя квантовая механика распределяет силы осциллято­ров между несколькими уровнями, сумма этих вкладов поглощения должна быть равна классически определенной величине. Поглощение в системе из-за оптических переходов между основным уровнем |1) и произвольным числом уровней [/) дается обобщением (3.39)[5]:

«(«) = #, 2 Ч Ж /., Цсо - соп) (3.41)

У=1 ^0гпспор