Линейная комбинация атомных орбиталей: модель жесткой связи
В главе 1 мы видели, что собственные состояния двух идентичных, атомов, обладающих идентичными энергетическими уровнями, гибридизируются, когда они сводятся вместе, порождая уровни связи и антисвязи с отличными собственными энергиями. Эти уровни разнесены на энергетической шкале на величину, связанную со степенью перекрытия (в данном случае обратно скоррелированную с физической величиной перекрытия) между собственными состояниями атомов. Теперь мы покажем, каким образом можно распространить эту процедуру на описание всего кристалла и каким образом с использованием данной модели можно подойти к понятию разрешенной и запрещенной энергетических зон. Этот подход полупроводниковой зонной структуры основан на значимости полупроводниковой зонной структуры и называется моделью жесткой связи (рис. 5.Б.1). Целью этой модели является отыскание кристаллических состояний с использованием линейных комбинаций образующих систему атомных орбиталей. Рассмотрим одномерную периодическую последовательность идентичных атомов. Начнем с предположения, что атомы достаточно отдалены друг от друга, чтобы пренебречь влиянием потенциала любого близлежащего атома на соседний атом.
Гамильтониан электрона в поле потенциала атома /, расположенного в решетке при 1а есть:
И, =^1+к(х-м) (5.Б.1)
|
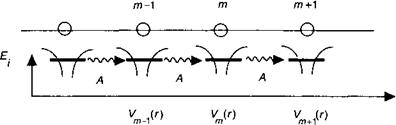
Рис. 5.Б.1. Одномерная модель кристаллического потенциала. Орбитали каждого атома кристалла связаны с соседним интегралом перекрытия, что позволяет электронам переходить от атома к атому за счет туннелирования. |
|
= 0 |
|
V H2(k-G)2 |
|
Е{к)- |
|
2т |
|
|
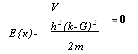 |
|
|
|
Это уравнение допускает два набора решений секулярного уравнения, которые с небольшими усилиями можно получить в виде:
|
E(q) = |
|
2т |
|
2 G Q |
|
2 Л |
|
|
|
|
Где <7 = & — (7/2. Мы вводим еф что представляет собой энергию, которой обладал бы свободный электрон при к = <7/2, т. е. ес = Н 2( <7 /2)2/2т. Для малых значений q уравнение (5.А.9) принимает вид:
|
(5.А.10) |
![]()
|
2т |
![]() + 2h - " V
+ 2h - " V
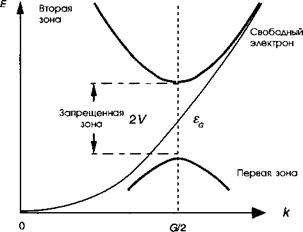
Рисунок 5.А.2 описывает решения уравнения Шредингера в виде (5.А.7). Мы видим, что можем выбрать по нашему желанию либо описание зонной структуры по всем зонам Бриллюэна, либо привести всю зонную структуру в первую зону Бриллюэна с соответствующим индексированием зон. Последний из подходов получил название схемы редуцированных зон, и он используется наиболее часто. На этом рисунке особо следует выделить ряд существенных моментов. Во-первых, вдали от границ зоны Бриллюэна зонная структура приобретает вид, характерный для энергетической дисперсии свободных электронов (что может быть показано). Во - вторых, ширина запрещенной зоны величиной приблизительно 2 ^обусловлена снятием вырождения между волнами &кг и eI(*_G)r. Отметим также, что дисперсионное соотношение E(q) является параболическим по q(~q2), что позволяет найти в рамках этой модели величину эффективной массы в виде:
|
Рис. 5.А.2. Существенные особенности модели почти свободных электронов. Периодическое возмущение кристаллическим потенциалом снимает вырождение вблизи краев зоны Бриллюэна (<7/2 = п/а), что приводит к возникновению запрещенной зоны. Полутоновые кривые получены приведением энергетических кривых Е(к) в первую зону Бриллюэна — это называется схемой зонного редуцирования. |
Таким образом все атомы обладают теми же самыми энергетическими уровнями Еп и теми же самыми смещенными собственными функциями:
1Л>'> = Дх) = ¥п(х ~ 1а) (5.Б.2)
Теперь сблизим атомы и попробуем найти стационарные состояния и собственные энергии Е для гамильтониана электрона в кристалле:
Я =|^ + 5>(*-''я) (5.Б. З)
Поскольку базис волновых функций у/п является полным, мы можем выразить гамильтониан (5.Б. З) в виде матрицы. Для этого внимательно посмотрим на различные
Члены — диагональные члены (/, пН'1, п) даются выражением:
|
(5.Б.4) |
![]() (я, іНп, і) = Е„ + (я, іу{х - х,п, /)
(я, іНп, і) = Е„ + (я, іу{х - х,п, /)
Член в сумме не зависит от / и приводит к сдвигу энергии. Таким образом этот член не имеет особого физического значения и им можно пренебречь.
В том, что касается недиагональных членов, нас интересуют только те члены, которые соответствуют ближайшему соседу:
(я, /|#| л, / ± 1) = £„(л, /| я, / ± 1) + / у{х - •*,) я, / ± 1) = (я, /У(х - х,} л, / ± 1) = - Ап
(5.Б.5)
|
(5.Б.6) |
![]() В выражении (5.Б.5) мы пренебрегли перекрытием между орбиталями вида (я, /|л, / ± 1) и оставили в сумме только члены Ап, соответствующие туннелированию между ближайшими соседями. С учетом этого предположения гамильтониан, описывающий электроны в кристалле, может быть разбит на независимые гамильтонианы для каждого невозмущенного энергетического уровня Е:
В выражении (5.Б.5) мы пренебрегли перекрытием между орбиталями вида (я, /|л, / ± 1) и оставили в сумме только члены Ап, соответствующие туннелированию между ближайшими соседями. С учетом этого предположения гамильтониан, описывающий электроны в кристалле, может быть разбит на независимые гамильтонианы для каждого невозмущенного энергетического уровня Е:
|
Е„ |
-А |
0 |
0 |
|
~А |
-А |
0 |
|
|
0 |
-л |
Е„ |
-А, |
|
0 |
0 |
-К |
|
= |
В этом случае стационарные волновые функции даются выражением:
|
(5.Б.7) |
|
(5.Б.8) |
![]() При этом коэффициенты Сп. даются уравнением Шредингера, т. е. решениями системы уравнений:
При этом коэффициенты Сп. даются уравнением Шредингера, т. е. решениями системы уравнений:
-АЯСЯ',_1 + ЕЯСЙ',-АЯСЯ'М=ЕСЯ'/
~ АпСп і + Е пСп /+1 — АпСя і+2 = ЕСЯшМ
Где £есть энергия новых стационарных состояний. В уравнении (5.Б.8) мы узнаем рекуррентные соотношения для ряда Фибоначчи, которые допускают решения в виде:
(5.Б.9)
Где х. = іа. Таким образом, мы можем обозначать новые собственные состояния кристаллического гамильтониана как у/к п. Легко показать, что эти функции экви
Валентны функциям Блоха—Фуке, полученным в (5.Б.8) (смотрите рис. 5.Б.2). Подставляя (5.Б.9) в (5.Б8) мы находим энергии для блоховских функций у/к :
Еп(к) = Еп - 2Асоь(ка) (5.Б.10)
Таким образом, стационарные состояния располагаются в энергетических зонах и синусоидально зависят от к. Схематически эти зоны изображены на рис. 5.Б. З. По сравнению с другими моделями эта модель дает ряд преимуществ, а именно большую степень предсказуемости.
|
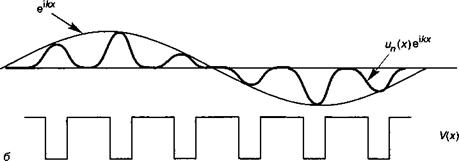
Рис. 5.Б.2. Функции Блоха—Флоке, описывающие стационарные состояния электронов в условиях периодического потенциала, представляют собой линейные комбинации изолированных атомных орбиталей (а), взвешенных на коэффициенты, представляющие бегущую волну в кристалле (б). |
|
Е(к)
|
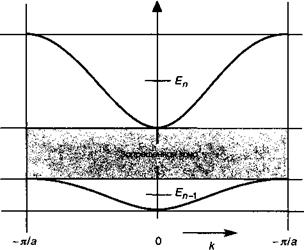
Рис. 5.Б. З. Разрешенные синусоидальные запрещенные зоны, полученные в рамках модели жесткой связи. Наличие запрещенных зон подтверждает тот факт, что разрешенные зоны не перекрываются.
Зоны имеют химическую природу и возникают вследствие гибридизации уровней, расширенных в зоны за счет туннельных эффектов между соседними атомами. Эта картина нас более удовлетворяет (и она ближе к действительности!) по сравнению с использованной в модели почти свободных электронов. Мы более ясно понимаем, почему зона проводимости в кремнии характеризуется синглетными состояниями 8р3 и почему валентная зона обладает свойствами гибридизированных триплетных состояний. К тому же мы лучше понимаем природу вырождения валентной зоны.
Причиной возникновения запрещенных зон является незаполненная область между состояниями Еп, возникающая после снятия вырождения. Если уширение зон превышает энергетический интервал между уровнями Еп, зоны соприкасаются и при этом запрещенные энергетические зазоры не возникают.
Чем более глубоки энергетические состояния (малые п), тем больше потенциальные (или туннельные) барьеры, которые разделяют состояния близлежащих атомов, и тем меньше величина Лп, что следует из интегралов туннелирования. В результате этого более глубоко лежащие энергетические зоны существенно уже (имея ширину 2Ап) по сравнению с более высоко лежащими зонами.
Вблизи экстремумов зон дисперсионные соотношения Е(к) являются параболическими, и они приводят к эффективной массе:
(5.Б.11)
|
|
И вновь мы обнаруживаем, что эффективная масса mcff обратно пропорциональна ширине разрешенной зоны.