Лазеры с распределенной обратной связью (ОРВ-лазеры)
Как это уже обсуждалось в разделе 13.8, полупроводниковые лазеры могут генерировать одновременно на большом количестве продольных мод. Однако, такое многомодовое функционирование нежелательно в целом ряде применений, поскольку оно приводит к: временному уширению в оптических волокнах, проблемам коллимации пучка и т. д. Таким образом, в таких случаях за счет использования зеркал с большой спектральной селективностью выгодно выбрать одиночную моду, которая испытает лазерное усиление. Такие зеркала могут быть реализованы за счет использования распределенной обратной связи. В данном случае идея заключается в том, чтобы встроить в лазерный резонатор модулированную волноводную структуру с периодом А (смотрите рис. 13.А.1). Такое периодическое возмущение, аналогичное брэгговскому зеркалу (смотрите дополнение 9. Г), действует подобно фильтру с очень большой селективностью. Формализм для описания оптической моды в пространственно модулированном волноводе был представлен в дополнении 9. Б. Сейчас же мы напомним основные результаты.
Обозначим соответственно как и ^"(^амплитуды оптических мод /с кон
Стантой распространения Д, распространяющихся направо и налево. Периодическое возмущение приводит к энергетическому обмену между волнами, распространяющимися налево и направо, как это описывается системой уравнений (9Б.6):
— а; (<;) = - (г ) е2‘4Л
Здесь Д/? есть член рассогласования фаз, определяемый соотношением:
ЬР = Р,-!т (13.А.2)
А
Только моды / с Д/?~ 0 могут распространяться в структуре. Обозначим как сов и /Зв частоты и константы распространения, которые удовлетворяют брэгговскому условию А/3 = 0. Константа связи g (не путайте с усилением!), которая описывает
|
0 |
2 = |
|
|
Р _п_л |
І_гі |
Alo.5Gao.5AS А^о^ао 7Ав |
|
ВаМ |
||
|
П Alo.3Gao.7As |
|
-------------------------- ► А+ «---------------------------- А~ |
Рис. 13.А.1. Поперечное сечение лазера с распределенной обратной связью. Содержание А1 на диаграмме носит условный характер, предполагающий возможный состав слоев.
|
|
Эффективность связи между волнами, распространяющимися налево и направо, может быть записана (9. Б.6б) в виде:
+оо
8 = — [(х]Е,(хУ<1х (1Э. А.З)
Здесь со есть частота электромагнитной волны, £м(.х) — функция относительной (модулированной) проницаемости в области дифракционной решетки, Е^х) есть распределение электрического поля для моды /, а р0 — есть нормировочная константа, необходимая для получения однородного уравнения (р0 = 1 Вт м-1). С уче
Том наличия усиливающей среды (с коэффициентом усиления у) (13.А.1) принимает модифицированный вид:
-%-А; = 1&4/е-2ЗД - уА;
* (13. А. 4)
-%-а; = - ы-е21Л* + уа;
Для решения этой системы уравнений проведем преобразование переменных:
А: - а7е~к
(13.А.5)
А; = а;е+*
Это приводит к новой системе уравнений:
1 (13.А.6)
—а; = dz
Формально, система (13.А.6) аналогична системе уравнений (13.А.1) с учетом преобразования А/?—> А/3 + у.
Таким образом, можно использовать результат дополнения 9.Б. Для этого нам необходимо детализировать граничные условия для амплитуд в волноводе. Предположим, что волна с амплитудой я,+(0) = а0 падает слева на вход дифракционной решетки (I = 0, смотрите рис. 13.А. 1), при этом никакая волна не падает справа на выход волновода (I = I) так, что а~{Ь) =0. В этом случае, уравнение (9.Б. 10) может быть записано в виде[29]:
(13.А.7)
А/(г)= А0 —------------- ^----- — ----------- —-{ЛИ [<?(г - I)]- {Ар + [<?(г - I)]}
(ьр + (6Ь)+ ЛЬ (дЬ)
На этот раз здесь коэффициент 3 дается (смотрите (9Б.9б) соотношением:
5 = у1ё2 + (у-Ар)2 (13.А.8)
Присутствие в экспоненте члена ±уц учитывает усиление в волноводе. Знаменатели в (13.А.7) выражают зеркальность периодической модуляции. Знаменатели в этом выражении исчезают, если:
^собЬ 31 = (у - 1Д/?)8тЬ 31 (13.А.9я)
Пороговое условие для ОРВ-лазера
|
|
В действительности, если это последнее условие удовлетворяется, система обеспечит ненулевой отклик даже при нулевом входе (12) — это и есть то, что характеризует лазерную генерацию. Для того, чтобы понять следствия этого условия для требований на усиление и согласование фаз, проанализируем (13.А.9) для брэгговской частоты сов, т. е. для А/3 = 0:
|
1 + |
![]() = tanh (yf^+fb) (13. А. 96)
= tanh (yf^+fb) (13. А. 96)
Когда усиление g стремится к бесконечности обе стороны этого последнего уравнения стремятся к единице, но при этом одна сторона от 1+, а другая от 1". Понятно, что (13.А.9б) не может быть удовлетворено и АР = 0 более не определяет распространяющуюся моду, т. е. усиление вводит новые условия для согласования фаз. Таким образом, необходимо решать уравнение (13.А.9) в комплексной плоскости.
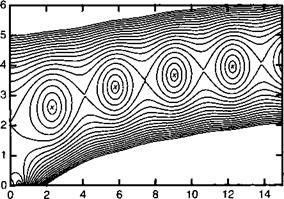
Рисунок 13.А.2 показывает контурный график l/|ЈcoshЈL — (у — iA/3)sinhSL2 для gL = 0,5. Чрезвычайно полезная программа MATHEMATICA, используемая для получения этого графика, приводится ниже:
GL=0,5;
DeltaL=Sqrt [д1_~2+(у-1*хГ2];
Den=1/Abs[deltaL*Cosh[deltaL]-(y-l*xSinh[deltaL]];
ContourPlot[Den, {x,0,15),{y,0,6},PlotPoints — > Ю0
ContourShading — > False, AspectRatio ->7]
Отметим, что произведение усиление—длина yL, необходимое для достижения порога, возрастает по мере отклонения от брэггвского условия Aj3L= 0. Это означает, что распределенная обратная связь благоприятствует только малым отклонениям от брэгговского условия. Для того, чтобы лучше понять это поведение решим это уравнение для случая сильного усиления, т. е. у» g.
Уравнение (13.А.9) может быть переписано в виде:
Это выражение может быть преобразовано следующим образом:
|
AfiL Рис. 13.А.2. Контурный график (13.А.9) в плоскости АрЬ — уЬ Решения этого уравнения располагаются в центрах замкнутых кривых. |
|
£ |
|
1 + |
|
*1 + |
|
У-ІА/З |
|
У - ІА0 |
|
£ |
|
У - ІД/? |
|
|
||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|
2пм |
|
1 21 2Ь |
|
Л Л_ А " |
|
2п^_ К |
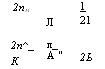 |
|
|
|
|
Спектральный зазор между двумя допустимыми модами составляет: ЛЯ = 2П,„ |
|
(13. А. 14) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
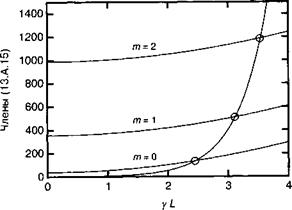
Рис. 13.A.3. Решения уравнений (13.А.15) для произведения gL{ = 0,5, дающие усиление, необходимое для генерации мод т = 0, 1 и 2. Видно, что наиболее благоприятные условия имеют место для моды т = 0, наиболее близкой условиям Брэгга. |
В пренебрежении паразитными потерями а условие лазерного порога реализу - ется при Kh„sholdI = 2. Выражение (13.26а) 4reshold = -1/21п(Лт1Лт2) показывает, что эта оптическая обратная связь соответствует коэффициентам отражения зеркал, определяемым RmlRm2 = е-4 = 0,02. Это совсем недалеко от величин порога, необходимых для лазеров с резонаторными зеркалами, полученными скалыванием, при этом для границ раздела GaAs/воздух RmlRm2 = 0,322 = 0,1. Понятно, что усиление у порога threshold может быть уменьшено за счет константы связи g, что соответствовало бы использованию зеркал с большими значениями коэффициентов отражения. Константа связи может быть увеличена за счет приближения дифракционных решеток ближе к активной области лазера. Это может приводить к значительным потерям, так как слишком близкое приближение дифракционной решетки к активной области будет приводить к дифракции света в излучательные («утекающие») волноводные моды. В общем случае оптимизация такой структуры требует использования численного моделирования.