Оптоэлектроника

Квазиуровень Ферми в неравновесной системе

Вплоть до настоящего момента мы рассматривали различные случаи, приводящие к уровням заселенности электронов и дырок в состоянии термодинамического рав­новесия. Вместе с тем во многих случаях уровни заселенности определяются нерав­новесными процессами. В самом деле, функционирование всех полупроводниковых приборов происходит в неравновесных условиях, являющихся следствием приложе­ния либо электрического поля, либо засветки структуры. В этих случаях электроны и дырки более не находятся в состоянии термодинамического равновесия друг с другом, а также с кристаллом матрицы. Таким образом, мы можем рассматривать внешний процесс, генерирующий электроны и дырки в полупроводнике со скоро­стью <7 и <7 (см-3 с-1) соответственно для электронов и дырок. Одновременно с этим предусмотрим существование рекомбинационного процесса, характеризуемо­го постоянными времени гиги приводящего к стабилизации заселенности элек­тронами и дырками до уровня, когда достигается баланс скоростей генерации и рекомбинации, т. е. <7я = п/тп и <7 = р/тр.

В этом случае стационарная концентрация электронов и дырок определяется соотношениями:

П = <7яг р = <7 г

Г во

В последней формуле мы предположили, что возникающие концентрации но­сителей превышают уровни тепловой генерации, т. е., что п » п0. Исключительно плодотворным оказалось предложение Шокли считать, что эти уровни заселеннос­ти по-прежнему можно описывать с использованием квазиуровня Ферми (шутливо названного Имреф, что произносится как Ферми, прочитанное в обратном поряд­ке!) Если система является невырожденной, исходя из (5.52) и (5.54) эти уровни определяются соотношениями:

Ег - кТ 1п

С„т„

(5.56а)

ЕР = Е„ + кТ 1п

Невырожденный квазиуровень Ферми

В том случае, когда система становится вырожденной, положение квазиуров­ней Ферми можно определить из (5.41) или:

Ееп-Ес+^пГ

(5.56 б)

ЕГ, = Е>-Т=-Ь *2рУ3

Вырожденный квазиуровень Ферми

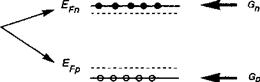
Понятно, что при (7 г » п0 и От» р0 квазиуровни Ферми не совпадают (смот­рите рис. 5.22) и на самом деле отделены от уровня Ферми на величину:

(ЕГп-Ег)-{ЕРр-Ег)=кТп

Это последнее соотношение позволяет нам рассчитать смещение квазиуровня Ферми в функции скорости накачки и различных рекомбинационных времен. Это уравнение занимает центральное положение в физике полупроводниковых лазеров, тему которых мы рассмотрим позже в главе 15.