Квантово-размерные фотоприемники
В разделе 8.6 мы уже видели, каким образом квантование движения электронов в направлении, перпендикулярном границам раздела в квантовых ямах, например, на основе системы GaAs/AlxGa, _xAs приводит к появлению энергетических подзон. Если такие квантовые ямы имеют я-тип проводимости (с эффективной двумерной концентрацией ps, выраженной в см-2), в соответствии со статистикой Ферми—Дирака дополнительные электроны начинают заполнять эти подзоны, начиная с основной подзоны ег В том случае, когда фотоны падают на квантовую яму, они обладают преимущественными возможностями для реализации электронных переходов между подзонами проводимости.
Возможно проявление двух типов оптических переходов:
> Переходы между связанными состояниями е, -> е2 (переходы из связанного состояния в связанное состояние). В разделе 8.6 мы видели, что такие переходы приводят к практически моноэнергетическим особенностям поглощения, а именно поглощаются только фотоны с энергией в пределах спектрально уширенного (на величину АГ) распределения в окрестности Иу=[18]£2 — ех = е12.
В этом случае коэффициент поглощения в квантовой яме дается (8.876):
А = *я1&РгЬ_ --------- *Г/* /(в) (11.57а)
П Пэс V12 " ЬУ) + (ПГ)
Мы напоминаем, что Z0 есть вакуумный импеданс (377 Ом), пх — коэффициент преломления полупроводника, 1п ~ дипольный матричный элемент (аппроксимация этого параметра приведена в З. Г.24) и его типичная величина имеет порядок 1 нм), д есть угол между осью освещения вектором нормали квантовой ямы. Как видно из раздела 8.7.2 функция Д#) изменяется как 8Ш[19]0/со80 до тех пор, пока поперечное сечение светового пучка поверхности детектора остается в пределах его поверхности. Зависимость зт2# следует из правил отбора для кц, как это поясняется рис. 8.13.
► Переходы из связанного в свободное состояние. Они доминируют, когда имеется лишь одна подзона в квантовой яме (смотрите (З. Г.27)). В этом случае переходы происходят между локализованными состояниями в квантовой яме (энергетический зазор между барьером и дном зоны проводимости составляет е{ = Ес — е{).
В этом случае коэффициент поглощения дается интегралом (11.57а), который берется состояниями континумма |в зоне проводимости барьера. Состояния |&) обладают энергией Е/= Йк2/2тс над дном зоны проводимости барьера, где тс — эффективная масса в зоне проводимости. В дополнении 1.А мы видели все сложности, связанные с нормировкой состояний континуума и необходимостью введения вирутального ящика шириной /,Пс1 для того, чтобы осуществить такую нормировку. Для расчета поглощения в квантовых ямах, связанного с переходами из связанного в свободное состояние, мы должны ввести следующий интеграл:
|
ПГ/7Г -1 2 + (11.576) |
![]()
|
А = ps^-ho)[^-{k, z 11)Г |
![]() ?----------- d kjiЯ)
?----------- d kjiЯ)
Мы напоминаем, что здесь Z, fict//r — одномерная плотность состояний импульса в континууме (смотрите дополнение 1.А. Выражение (11.576) может быть представлено в виде, более пригодном для расчетов за счет введения дипольного объема z(E) который возникает как предел Lfict|(/:Jz|l)|2 при LRct ->°о, с последующим интегрированием по энергии конечных состояний Ef, что приводит к выражению:
А = |цtd(/7V, Ef)bEff(Я) (11.58а)
О
Здесь: aD есть дифференциальное поглощение, определяемое следующим образом:
AD{hv, Ef)=q2^c P'ZsLhv&дr-?---------------------------- (П.586)
2 Ь2 пх д/£> [Ef-{hv-e^+(tiTj
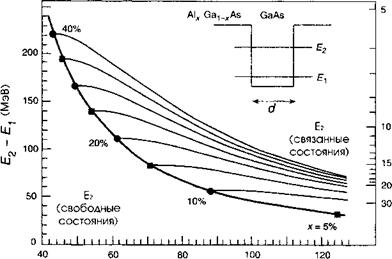
Тонкие линии на рисунке 11.17 представляют энергии е2 — ех межподзонных переходов между связанными состояниями в квантовых ямах на основе GaAs/Al^Ga, ^As в функции содержания А1 х, а также толщины ямы.
Жирная линия представляет геометрическое место точек, соответствующих концентрации и толщине, приводящих к квазирезонансной ситуации, когда энергия первого возбужденного состояния е2 располагается как раз на уровне вершины
квантовой ямы (и соответственно у дна барьера). Именно такая конфигурация и используется в квантово-размерных фотоприемниках.
Безусловно, в такой ситуации структура обладает двойным преимуществом: сила осцилляторов для таких переходов все еще играет важную роль, что очень близко к ситуации с переходами между связанными состояниями, и в то же время возбуждаемый электрон может свободно распространяться по возбужденному состоянию, что аналогично характеру переходов между свободными и связанными состояниями. Таким образом, рис. 11.17 показывает, что мы можем подобрать параметры квантовой ямы и условие квазирезонанса будет обеспечено в спектральном диапазоне от 5 до 20 мкм, т. е. перекрывать часть дальней ИК-области спектра. Аналогичным образом средняя ИК-область спектра может быть освоена с использованием квантовых ям на основе 1пСаА$/АЮаА8.
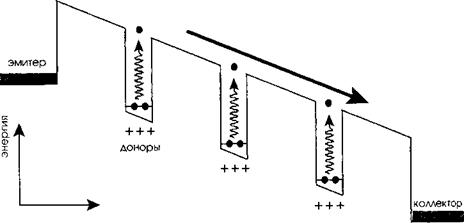
Электроны, возбужденные в континуум барьера, удаляются электрическим полем, что приводит к фототоку. Электрическое поле Е возникает за счет приложения соответствующего внешнего смещения, например, через два сильнолегированных контактных слоя ваАз. Такая структура приемника излучения с набором квантовых ям представлена на рис. 11.18. Мы увидим, что увеличение числа квантовых ям приводит к тривиальному повышению полного уровня поглощения света, а также к увеличению полной квантовой эффективности и обнаружительной способности прибора.
|
* Прим. ред.: строго говоря узкополостным спектром фоточувствительности обладает достаточно широкий круг не только квантово-размерных фотоприемников. |
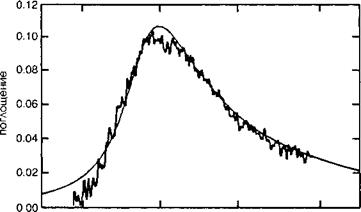
![]() При достаточно низких температурах электроны захватываются в основной квантово-размерной подзоне, и в идеальном случае система становится изолирующей. Под влиянием потока фотонов электроны фотоионизируются из квантовых ям и попадают в барьерные области, что приводит к фототоку, который может быть измерен амперметром. На рисунке 11.19 показаны рассчитанный (с использованием (11.58)) и измеренный спектры поглощения приемника излучения с набором квантовых ям. Следует отметить что по сравнению с другими типами полупроводниковых фотоприемников, квантово-размерные приборы являются узкополосными приемниками излучения*.
При достаточно низких температурах электроны захватываются в основной квантово-размерной подзоне, и в идеальном случае система становится изолирующей. Под влиянием потока фотонов электроны фотоионизируются из квантовых ям и попадают в барьерные области, что приводит к фототоку, который может быть измерен амперметром. На рисунке 11.19 показаны рассчитанный (с использованием (11.58)) и измеренный спектры поглощения приемника излучения с набором квантовых ям. Следует отметить что по сравнению с другими типами полупроводниковых фотоприемников, квантово-размерные приборы являются узкополосными приемниками излучения*.
|
С1 (ангстрем) Рис. 11.17. Энергии переходов в квантовых ямах СаАБ/ЛЮа, _ хАб между связанными состояниями (тонкие линии), между свободными и связанными состояниями (затемненная область) и между связанными и квазирезонансными состояниями (жирные кривые). |
|
Фотовозбужденный электрон Фототок
Расстояние Рис. 11.18. Схема функционирования приемника излучения с набором квантовых ям. |
|
|
|
100 |
|
120 |
|
140 |
|
160 |
|
Энергия (МэВ) Рис. 11.19. Экспериментальный и расчетный спектры поглощения приемника излучения с набором квантовых ям в планарной волноводной геометрии (в= 90°). (С разрешения Я. Ьис@ТНАЬЕ8). |
Для описания работы квантово-размерных приемников излучения могут быть использованы две модели (рис. 11.20)
•
|
(11.59) |
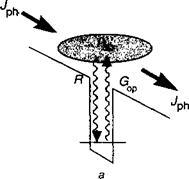
![]() Модель фотопроводника (рис. 11.20а). Скорость генерации на квадратный сантиметр в одиночной квантовой яме с коэффициентом поглощения под воздействием потока фотонов Ф0 есть:
Модель фотопроводника (рис. 11.20а). Скорость генерации на квадратный сантиметр в одиночной квантовой яме с коэффициентом поглощения под воздействием потока фотонов Ф0 есть:
Сор = Реа
Здесь ре есть вероятность того, что фотовозбужденный электрон будет возбужден в континуум барьера и удален электрическим полем. В стационарном состоянии эта скорость может быть компенсирована скоростью захвата, которая поддерживает заполнение квантовых ям электронами. В этом случае скорость рекомбинации определяется соотношением:
РгР
-7-
|
|
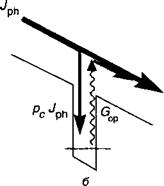 Рис. 11.20. Две модели для описания переноса электронов через приемник излучения с набором квантовых ям: модель фотопроводимости (а) и фотоэмиссии (б).
Рис. 11.20. Две модели для описания переноса электронов через приемник излучения с набором квантовых ям: модель фотопроводимости (а) и фотоэмиссии (б).
Здесь г есть время захвата электрона в барьере квантовой ямой, а р20 — двумерная плотность фотовозбужденных носителей. Во время захвата г доминируют взаимодействия Фрелиха (смотрите дополнение 6.Б) и его типичное значение лежит в диапазоне от 1 до 10 пс. Предположение о равенстве друг другу (11.59) и (11.60) определяет двумерную плотность р2£>. Трехмерная концентрация носителей рю может быть получена в предположении о том, что носители однородно распределены по барьерному материалу с толщиной Ь так, что:
TOC o "1-5" h z Р)о=£^ = Мш1^± (1Ш)
Следуя той же самой схеме рассуждений, как и в разделе 11.2, мы находим, что фоточувствительность приемника излучения с набором квантовых ям есть:
И = ?71о«С, о« ,
Т т
Лнэч/ - и = = г С,
Ти Ь
Здесь: /71С^ есть квантовая эффективность одиночной квантовой ямы, тхт — время переноса электрона в барьере толщиной Ь со скоростью V, = //£*, а (71(^ есть однопроходное усиление фотопроводимости. Мы видим, что в этом последнем выражении чувствительность приемника излучения не зависит от числа квантовых ям. Этот достаточно удивительный результат есть следствие сохранения электрического тока. С другой стороны, мы увидим, что обнаружительная способность прибора с N квантовыми ямами пропорциональна л/М
• Модель фотоэмиссии (рис. 11.20б). При использовании этой модели ток определяется тем условием, что в стационарном состоянии поток носителей, захваченный квантовыми ямами р^^/ч находится в точном балансе с потоком фотоионизиро - ванных электронов вне ямы ре ог1(^Ф0. Коэффициент рс есть вероятность захвата для электрона, пересекающего квантовую яму. Полагая оба потока равными, получаем для фоточувствительности приемника излучения:
* = 77
Г - 1_
Умум _ Ре& 1<^ и 1 -
ГС
Мы видим, что выражения для чувствительности квантово-размерного приемника излучения, получаемые в рамках каждой модели, идентичны, если:
Рс 1
Это последнее выражение связывает время захвата квантовой ямы с вероятностью захвата электрона, пересекающего квантовую яму.
Пример-------------------------------------------------------------------------------------------------------------
Рассмотрим квантово-размерную структуру, подверженную воздействию электрического поля, возбуждаемого разностью потенциалов в 1 В на расстоянии в 1 мкм, т. е. с напряженностью 104 В см-1. Подвижность носителей в барьере составляет 102 см2 В-1 с-1 при толщине барьера Ь между последовательными квантовыми ямами 25 нм и времени захвата г = 10 пс. В этом случае скорость V, составляет 106 см с“1, а вероятность захвата рс равна 0, 25. В этом случае усиление фотопроводимости квантовой ямы <71(^ в предположении вероятности ионизации ре = 1 составляет 4.
При использовании согласователя с дифракционной решеткой коэффициент поглощения для типичной квантовой ямы составляет = 1% на длине волны Л = 10,6 мкм (117 мэВ). В этом случае фоточувствительность такого квантоворазмерного приемника излучения составляет В = 4 х 10“2/0,117 = 0,34 А Вт'1.
Обращаясь к аспектам, связанным с обнаружительной способностью, мы видим, что шум приемника излучения с N квантовыми ямами определяется (11.А.42):
"Рс
Темновой ток /0 может быть получен, если мы сначала рассчитаем концентрацию р20 А термически активированных носителей в барьере зоны проводимости. Ранее мы видели (8.43), что эта концентрация определяется выражением:
П - 1 тс - 1 тскТ _ Пс (Е,-Е,)/кТ П 1 66)
Р™Л ~ ЬянЧ* йЬ - Ь яй2 6 'Iе и }
Е(
Здесь пс есть критическая концентрация (8.43) в зоне проводимости, а уровень Ферми Ер получается, если предположить, что квантовые ямы легированы до концентрации р5 так, что (смотрите 8.45):
При этом Ее — сть энергетический зазор между уровнем барьера и уровнем Ферми. Для квазирезонансного приемника излучения при Ну мы должны иметь:
Е'-Ег =Ну-(Ег-£1)=Ну------------ (11.67 б)
Тс / т
Темновой ток получаем, положив 10 = А/0 = Адрю при этом выражение для обнаружительной способности (в предположении ре « 1)дается в виде:
£*«-7-,--------------- ?---------------- (П-68)
42(2 - дК/Л^
Так что:
|
И = |
|
Л ] {)\_____________ N1 |
|
Иу |
|
|
|
|
Обнаружительная способность квантово-размерной структуры
Из этого выражения мы и получаем выше упомянутую зависимость от >/М Последнее уравнение показывает также, что, если мы увеличиваем уровень легирования квантовых ям, мы можем ожидать улучшения квантовой эффективности за счет увеличения а1(^ (смотрите (11.58)). Однако, высота теплового барьера Ес — Ег уменьшается в соответствии с (11.676). Таким образом, существуют компромиссные условия, оптимизирующие обнаружительную способность (11.69).
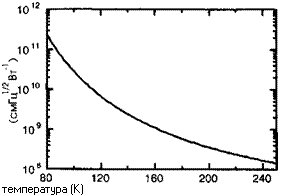
Рисунок 11.21 демонстрирует температурную зависимость обнаружительной способности на длине волны 8,5 мкм для квазирезонансного приемника излучения. В рассматриваемом случае мы наблюдаем зависимость еЛ1'/2*г, типичную для всех квантовых приемников излучения.
|
Температура (К) |
|
О 0 0 ю о о о с о С: 0 1 3 8 З: £ А О X Ю О |
![]() Рис. 11.21. Температурная зависимость обнаружительной способности квантово-размерной структуры (# = 50) в предположении квантовой эффективности 1% на квантовую яму.
Рис. 11.21. Температурная зависимость обнаружительной способности квантово-размерной структуры (# = 50) в предположении квантовой эффективности 1% на квантовую яму.
Широко распространенный интерес к квантово-размерным приемникам излучения обусловлен двумя принципиальными преимуществами:
• Длина волны фотодетектирования может быть подобрана по желанию. Для этого необходимо только выбрать определенные значения толщины квантовой ямы и содержание А1 в барьере в процессе синтеза (этот аспект проектирования называется квантовой инженерией).
• Стандартные методы микрообработки наиболее хорошо подходят для производства крупноформатных матриц приемников излучения, которые в отличие от диодов Шотки обладают хорошей обнаружительной способностью.
Наконец, заметим, что поскольку квантово-размерные приемники излучения не могут регистрировать излучение при нормальном угле падения, то должен быть найден способ, обеспечивающий эффективное участие фотонов в меж- подзонных переходах. Это может быть достигнуто за счет формирования решеточного устройства ввода на поверхности приемника излучения травлением (смотрите рис. 11.22).
Пример -------------------------------------------------------------------------------------------------------------
Рассчитаем обнаружительную способность для квантово-размерной структуры при 77 К в предположении следующих физических параметров:
Ь V = 0,155 эВ (Л = 8 мкм)
N=50 Рс = 0,25 V, = 106 см с-1
Тс/п:П2 = 2,78 х 1013 эВ1 см"2 и пе = 7, 2 х 1011 (7/300) см"2
/= 250 А
Р5 = 5 х 1011 см-2
|
Контакт пикселя общий контакт
Падающее ИК-излучение |
|
Ш |
Подложка ОоАб |
■■■■ слой МОУУ |
|
1 контактные слои ОоАб |
Диэлектрический слой |
|
|
Контакты |
|
Рис. 11.22. Одиночный пиксель матрицы приемников излучения с набором квантовых ям. Решеточное устройство ввода перенаправляет перпендикулярно падающее излучение для увеличения перекрытия с разрешенными межподзон - ными переходами. |
Ес-Ег= 0,155эВ-5х 10“ /2,78х 1013 эВ = 0,155-0,018эВ = 137мэВ При этом обнаружительная способность определяется выражением (11.69):
0* ю-2
0, 138x1,6x10'''’ Дж л/50
.Ь х 0,25 х 106 см с'1 х Т^х^/ЗОО^см;* е-(° |38/8-6М0 <г)
V 250x10"8 см
Или 3 х 1011 см Гц1/2 Вт-1 при 77 К.