Оптоэлектроника

Квантовая яма

С использованием двух гетеропереходов теперь становится возможной реализация одно­мерного профиля потенциала вдоль направления роста для электронов, соответствующе­го квантовой яме, исследованной в главе 1.

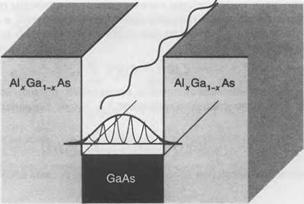
Рис. 8.4 демонстрирует наиболее изученную к настоящему времени структуру с квантовой ямой, состоящую из слоя квантовой ямы СаАз, заключенного между двумя более широкозонными барьерными слоями А1хСа1 _хАб. При х < 0,4 разрыв зоны проводимости пропорционален содержанию АІ, так что АЕс ~ х х 836 мэВ. Подбирая содержание А1 и толщину слоя ваАз в процессе роста, мы можем со­здать квантово-размерную структуру, обладающую электронными свойствами, со­ответствующими требованиям пользователя — на практике это называется кван­товой инженерией.

Для электронов в зоне проводимости слои АЮаАБ образуют потенциальные барьеры высотой Ув = АЕс. В этом случае уравнение Шредингера приобретает вид:

При этом величина V(z) равна нулю в яме и Увв барьерах. Как эффективная масса, так и потенциал зависят только от z, в то время как в направлениях х и у (парал­лельно границам раздела) эффективные потенциалы не изменяются. Следователь­но ^г) может быть записана в виде:

#г) = CK(^)exP(iK R) или R = (*’ У) и К = (Л к )

В этом выражении огибающая волновая функция представляет свободное движе­ние электронов в плоскости, параллельной границам раздела, а СпК(%) определяется одномерным уравнением Шредингера:

(8.27)

Обозначая эффективные массы в яме и барьере соответственно как ту> и тв, находим:

Для малых /^корректировка «потенциальной энергии» из-за изменения эффективной массы пренебрежимо мала. Практически во всех случаях ей пренебрегают из тех сообра­жений, что функция СпК(д в этом случае становится независящей от К и подчиняющейся простому уравнению:

,2

D П2 d / dz2m*(z)dz+ Z_

П2К2

2т...

Если бы эффективная масса не зависела от материала, это уравнение было бы тем же самым, что и уравнение, полученное для квантовой ямы, исследованной в главе 1. Поскольку как эффективные массы, так и потенциалы постоянны в обла­стях, разделенных гетеробарьерами, решение (8.29) получить нетрудно.

Рассмотрим границу раздела при z = L/2 для е < VB в области ямы. Решением является комбинация двух плоских волн:

C(z)=atikk~L/2)-bt-u(z-L/2), z<L/2 (8.30)

При этом h 2k2/2mw = е.

В области барьера для z > L/2 допустимое решение содержит затухающую экспоненту:

C(z)=ct-^-L/2 z> L/2 (8.31)

С h1k1/2mB = VB-e.

Используя условия непрерывности при Z— L/2, мы находим:

1=е-2м = (8 32)

В W„/mB)c + 1 к

С учетом (8.30) выражение (8.32) говорит нам о том, что электронная волновая функ­ция сдвинута по фазе на 2ф в результате отражения от границы раздела при z = L/2. В этом случае 0 дается соотношением:

Sin ф = -j--------------- ------------ ^777 (8.33)

{[(mw /тв)с]2 + к2}

С учетом того, что область ямы начинается у границы раздела при z = — L/2, фаза плоской волны, распространяющейся слева по направлению к границе раздела спра­ва, увеличивается на kL, при этом отражение увеличивает фазу на 2ф, при этом об­ратный проход отраженной волны к —L/2 приводит опять к добавлению kL. Нако­нец, отражение при z — —L/2 обусловливает второй фазовый сдвиг величиной 2ф. Для стационарного состояния полный фазовый сдвиг после полного цикла обраще­ния должен быть равен 2пж, где п есть целое число. Это приводит к условию, что 2ф= пж~ kL или вновь:

2 . к k. L к /о

—arcsin - j-------------- ------ yjt = п —-------------------------------- (8.34)

Я {[(^ /твУ~ +К2} ’ я к0

При этом h2k2/2mw = VB

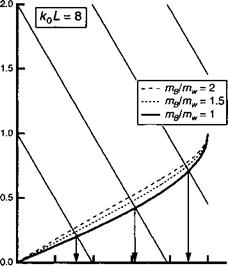
Графическое решение на рис. 8.5 показывает, каким образом это условие выполняется для нескольких значений mB/mw.

При mw = тв решения на рис. 8.5 эквивалентны тем, которые представлены на рис. 1.2.

В этом случае энергия стационарного состояния, которое мы можем обозна­чить как |яК) в соответствии с (8.29), дается соотношением:

Ь2К2

E"K=Ј"+4t~ (8-35)

Где £ представляют собой дискретные значения энергии и решения (8.29), а К является непре­рывной величиной в плоскости (Кх, Ку). Эти состояния организованы в виде подзон, как это показано на рис. 8.6. Каждая подзона включает в себя ансамбль электронных состоя­ний, обладающих тем же самым состоянием квантованного движения, перпендику­лярного границам раздела, а также непрерывно изменяющимися волновыми вектора­ми К, соответствующими их беспрепятственному движению в плоскости. Для описа­ния ансамбля электронов, занимающих такую зонную структуру, используется понятие двумерного электронного газа.

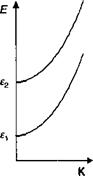
Рис. 8.6. Квантово-размерная структу­ра (а), показывающая две подзоны в яме с соответствующими огибающими фун­кциями (перпендикулярными границам раздела) и энергетические спектры (б).

Рис. 8.5. Графическое решение (8.34). Решения даются точками пересечения наклонных линий п — kL/n и функ­ций arcsin.

Важно отметить, что волновые функции по-прежнему допускают разделение переменных, поскольку потенциал зависит только от I. Форма V (г) имеет значение только при определении энергетических минимумов подзон еп. Энергия еп называ­ется также энергией ограничения. Таким образом, концепции подзон и энергий огра­ничения остаются справедливыми во много большем числе систем по сравнению с рассмотренной здесь симметричной квантовой ямой.