Оптоэлектроника

Квантовая модель квадратичной нелинейной восприимчивости

В разделе 12.2 в рамках механической модели нелинейной оптики мы смогли уви­деть, каким образом нелинейная восприимчивость второго порядка возникает вслед­ствие асимметрии механических потенциалов (12.1), ограничивающих движение электронов, которое возбуждается электромагнитными волнами. Хотя интуитивно эта модель кажется продуктивной, она находится в сильном противоречии с кван­тово-механической природой электронов в среде. В связи с этим мы предлагаем здесь вывод квантового подхода. Очень эффективный и прогностический форма­лизм, который нам предстоит разработать, основан на подходе матрицы плотности, представленном в разделе 1.7.

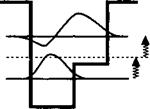
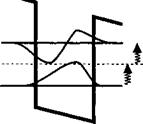
Рассмотрим квантовую систему, описываемую гамильтонианом Н0 и обладаю­щую спектром дискретных невырожденных состояний |/) с энергией Е. такой, что H0i) = EJi). Примеры таких систем показаны на рис. 12.А.1. В условиях теплового равновесия соответствующая матрица плотности представляет собой диагонализи - рованную матрицу р0 с диагональными элементами р..(0) = п., равными заселенности уровней Е. в соответствии со статистикой Ферми—Дирака. Плотность заселенности выражается в единицах «см-2» или «см-3» в зависимости от того двумерная или трехмерная системы рассматриваются. После чего система возбуждается электро­магнитной волной с электрическим полем, которое имеет вид:

£(/)= Ёсш' + Ёс-Ш1 (12.А.1)

В рамках дипольной D • Р-аппроксимации (смотрите главу 3) взаимодействие между квантовой системой и электромагнитным полем описывается гамильтониа-

Рис. 12.А.1. Несколько примеров асимметричных квантовых систем, основанных на квантовых ямах.

Ном H(t) = —qzE(t). Под влиянием этого нестационарного возмущения эволюция элементов ptJ матрицы плотности описывается уравнением Шредингера:

— = — [Н0 ~<1zE(t), р- Г()(р - р(0))„ (12.А.2)

?t ъ

Для упрощения мы предположим, что для описания системы нам требуются только две скорости релаксации Гу: Г, = /Т1 для i = j есть скорость релаксации заселенно­сти (неупругий механизм), т. е. скорость выхода электрона из возбужденного со­стояния, а также Г2 = /Т2 — недиагональная скорость релаксации или константа дефазировки, соответствующая упругому рассеянию электронных фаз по различным состояниям. Матрица плотности может быть представлена в виде ряда по электри­ческому полю в следующем виде:

<12л-з>

П

При этом:

UzE(f), Р'”1], (12.А.4)

Dt Ь Ь

Член порядка п(р(п)) действует в дифференциальном уравнении по р<я+1) как член источника. Следуя рекуррентной последовательности, мы видим, что вклад электрического поля E(t) в дипольный матричный элемент р.}п) является полино­мом порядка п. В этом случае электрическая поляризация в направлении Oz дается средней величиной оператора qz полученного, как и другая наблюдаемая величина — (смотрите раздел 1.7) оценкой шпура pqz:

P(t)= Tr(qzp)= q^(zp = q^^ZitPk, (12.A.5)

/ i k

Таким образом, вклад матрицы плотности порядка п в электронную поляриза­цию является поляризацией я-ного порядка:

/>,'”(0=TiVv) (12.А.6)

В этом случае первые два элемента в разложении электронной поляризации P(t) системы получаются из члена полинома:

^(0= e0xmEt'a + saivE'c™ + к. с. + ел«Щ (12.А.7)

Здесь: z(1 2ш и Zq2) есть соответственно линейная и квадратичные восприимчиво­

Сти (для процессов генерации второй гармоники и оптического выпрямления). Член по 2о) связан с произведением членов по и ei<w/ в то время, как постоянный член является результатом произведения ei<y/ и e_i<y'. Член %0(2) порождает постоянное элек­трическое поле под влиянием электромагнитной волны, что соответствует явлению оптического выпрямления, и в этой книге мы не будем его более касаться. Нас инте­ресует лишь член генерации второй гармоники 2а) (или в более общем случае па)), т. е. выражения р(п) вида:

P(*)(t)= р(п)(а))е[пй* + у5(я)(- (o)t-[nml (12.А.8)

В (12.А.4) мы можем заменить член сЦ.(я+ l)/dt на i(п + 1 )(op. jn + 1). Более того, по­скольку гамильтониан Н0 является диагональным в базиое, сформированном его стационарными состояниями |/), мы имеем:

[я„, = X - X = {Е, - Е,)(р^‘>)„ (12.А.9)

К к'

Это приводит к упрощенному варианту рекуррентного соотношения в (12.А.4):

ДГ',(®)= —F--- g^ ^(12.А.10)

H^fi + )o)+

Здесь: а).. = (£. — Ej)/h есть боровская частота. Начнем с применения рекуррентного соотношения (12.АЛО) для п — 0. Это сразу дает:

Pd)(/)= pV)(a})eitt* + pw(-G))e-itt* (12А11)

При этом:

Д«> = S (12 д 12)

ДRfц + avJ-irJ

Здесь zy есть матричный элемент ztj = (*|г|/)- Подставляя это выражение в (12.А.5) и (12.А.6), мы получаем линейную поляризацию:

£(0=11у М £ (12.А.13)

H Lk [(б> + coki) - irw]

В условиях слабой освещенности и при разумных температурах (кТ < Еп - £,) заселенным будет только уровень |/), и, таким образом, только члены / или к = 1 дают вклад в линейную восприимчивость. Сравнивая это выражение с уравнением (12.А.7), мы находим, что линейная восприимчивость определяется выражением:

= ^У, К, <|2А|4>

E0h ш [(<a-<ьtl)-ir2J Это позволяет нам получить коэффициент поглощения как а = (Лт^"/па с т. е.:

Q<o_ у --------- r2J^il--------------------------------- (12.А.15)

NopЈ0ch М p)-cokY + r,2J

Или вновь:

А = _£Ж_У/4|_®_ --------------------- Ы£---------------------------- (12. А. 16)

2тпоре0с ы, 4<ок1 1(о)-а)к1У +Г22]

Здесь fkx = 2т(Ек — E^z^/h2 есть сила осциллятора для перехода |1) -> |к), что воспроизводит результат, полученный в главе 3, а именно, уравнение (3.41).

Следующая итерация (п = 1) дает нам квадратичную восприимчивость. Таким образом, начнем с элемента второго порядка матрицы плотности:

Ра)(() = + р£(- й>)е-2“* (12.А.17)

При этом р2^2) определяется (12.А.10):

Ы2:1=~,--------------- 1-------- Д9Z, ptn]tE (12.А.18)

HQco + <ац - irj

Проведем итерацию, подставляя (12.А.12) для /?(,) в последнее выражение, при этом находим:

ЬМ. = Il_______________ !_______ у z>'z'krn') у _Mih^hl]E2 (12.А. 19)

Й2 (2(О+Щ - ir#.) I / [(<»+»(,)- irj I [(<Ь+ 0„)~ ir„]|

Затем используем шпур оператора p{2)qz для того, чтобы найти электронную поля­ризацию второго порядка P(2)(t) (смотрите (12.А.6). Для определения квадратичной

Восприимчивости нам нужно лишь использовать уравнение (12.А.17), при этом (после исполнения нескольких акробатических номеров с индексами!) мы находим:

(12.A.20)

Несмотря на свой несколько сложный вид эта формула позволяет рассчитать квадратичную оптическую восприимчивость для любой квантовой системы, при этом особый интерес для нас представляют следующие два случая:

• Двухуровневая система. При пренебрежении антирезонансными членами в (12.А.20) в суммировании остаются лишь два члена, а именно те члены со + со.., для которых со0 > 0. Это дает для квадратичной восприимчивости:

„<2> = g'fa ~ П2)________ *12^2

Л 2 (О -> / . Ч//Ч

Є0Рг2 (со - co2l - T2)Q. co - со2ї - ІГ2)

Здесь: Sl2 = (2z2) — (1|$|1) = z22 ~ zu есть среднее смещение электронов вслед-

Ствие переходов с уровня |1) на уровень |2). Мы сразу видим, что, если система обладает инверсионной симметрией (или говоря более точно, если электроны на двух уровнях обладают тем же самым средним положением 1и = z22), то квадра­тичная восприимчивость сводится на нет. Вторым моментом является то, что квадратичная восприимчивость максимальна, когда достигает максимума произ­ведение 312. Для достижения максимума квадратичной восприимчивости необ­ходимо, чтобы средние положения волновых функций, описывающих состояния |1) и |2) были бы разнесены друг относительно друга на максимально возможное расстояние (^12 максимально). Взаимный компромисс между этими двумя проти­воречивыми требованиями может быть достигнут путем квантовой инженерии мо­лекул и квантовых ям для конкретных применений нелинейной оптики. Вдали от резонанса (со12 »со) выражение (12.А.21) может быть записано в виде:

(12.А.22)

Квадратичная восприимчивость двухуровневой системы

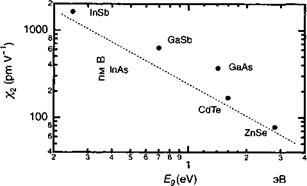
Величина в числителе представляет собой величину заряда в асимметричном объеме zX2Sl2. Из этой формулы мы видим, что квадратичная восприимчивость выражает­ся в единицах мВ-1 (а на практике в единицах пм В-1). Хотя это выражение и не было получено в контексте физики полупроводников, оно тем не менее дает по­лезную информацию по поведению этих материалов, поскольку можно рассмат­ривать зону проводимости и валентную зоны как если бы они представлялись двумя различными энергетическими уровнями, разделенными по энергии на Eg. Предполагая (в рамках данного рассмотрения) постоянными матричные элемен­ты Zy, мы видим, что можно ожидать изменение нелинейной восприимчивости полупроводников как 1 /Е Рисунок 12.А.2 иллюстрирует квадратичную нелиней­ную восприимчивость х2 Для различных полупроводников на длине волны 10,6 мкм в функции ширины их запрещенной зоны Eg. Зависимость, предсказываемая (12.А.22), удивительно хорошо выполняется несмотря на упрощенность модели, которую мы использовали и которая не учитывает изменяющуюся ионность хи­мической связи и т. д.

• Трехуровневая система. В случае трехуровневой системы с постоянным энергети­ческим зазором (Е2 — Е{ = Е3 — Е2 = fiQ) выражение (12.А.20) обладает четким максимумом, соответствующим двойному резонансу co~col2~ со23 * Q. В рассмат­риваемом случае в сумме (12.А.2) доминирует один член:

Vm = g3(", - пг)

/С 2(0

-------- Ч (12.А.23)

Е0ПЛ (со - Q. - ir2 д2б> - 2Q. - ir2)

И вновь, понятно, что произведение zl2z23z3l равно нулю, если система асимметрич­на. Вблизи резонанса (*у~£2) квадратичная восприимчивость принимает вид:

Zm _ = Ч_ 6»,- *»,)(*,,у,,) (12 А 24)

£0 (hr2/q)-

Выражения (12.А.22) для нерезонансной системы и (12.А.24) для резонансной сис­темы обеспечивают достаточно надежное предсказание величины нелинейной квад­ратичной восприимчивости в квантовых системах, таких как молекулы или асим­метричные квантовые ямы.

Пример-------------------------------------------------------------------------------------------------------------

1. Асимметричные молекулы. Выражение (12.А.22) позволяет рассчитать порядок величины нелинейной восприимчивости в среде, образованной молекулами с резо­нансом hcon вблизи 2 эВ с концентрацией 1028 молекул/м3, а также матричными элементами zl2 — 1 А и 612 = 0,1 Д. Отношение q/eQ составляет 1,8 х 10-8 В м. Среднее число молекул в z?2Sxl составляет таким образом 10 х (10-10)2 х 10"11 или 10"3.

Х{2) = 1,8 х 10"8 В м х 10"3/4 В2 = 4,5 пм В'1

Эта величина есть именно то, что приблизительно было обнаружено при иссле­довании неоптимизированных асимметричных молекул.

2. Асимметричные квантовые ямы. В главе 8 мы видели, что оптические межпод - зонные переходы в квантовой яме могут быть описаны как переходы между диск­ретными энергетическими уровнями. В этом случае электроны обладают эффек­тивной массой, связанной с их подзоной. В процесс можно ввести асимметричные композиционные градиенты в квантовых ямах с тем, чтобы обеспечить асиммет­ричность ограничивающих потенциалов (смотрите 12.А.1).

В качестве примера возьмем квантовые ямы со слоями GaAs толщиной 6 нм и Al01Ga09As толщиной 4,5 нм, разделенных барьерами Al04Ga06As толщиной 30 нм. Квантовые ямы легированы до уровня 2 х 1017 см-3, при этом коэффициент запол­нения составляет ’/4. Для расчета энергетических уровней Е{9 Е2, Е3, получаемых как решения одномерного уравнения Шредингера ((р2/2т* + V(z))i) = £]/), а также матричных элементов zl2, и z3l, может быть использована очень простая програм­ма MATHEMATICA. Эта система была спроектирована таким образом, чтобы обес­печить эквивалентность переходов Е2 — Ех и Е3 — Е2 с энергией перехода, эквива­лентной длине волны 10,6 мкм. Матричные элементы zl2 г>3 и z3l составляют соот­ветственно 2,1, 3,0 и 0,38 мкм. Отметим, что эти матричные элементы превышают соответствующие значения для молекул. Это связано с малой эффективной массой электронов в GaAs. Поскольку система является дважды резонансной для расчета
восприимчивости при резонансе может быть использовано соотношение (12.24). Мы находим, что:

(2) 1,6х 10'19 Кл 2х 10 23 м'3/4х(2,4х 10'27 м3) _

— = 777—---------------- Г-------------- / ' V-------------- = 22 ООО пм В"1 (12.А.24)

8,85 х 1012 Ф м'1 (Ю'2 В/

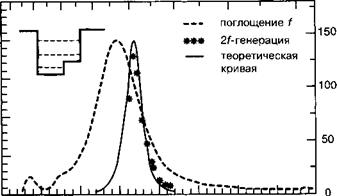
В заключение следует отметить, что значительные по амплитуде нелинейные оптические эффекты могут быть реализованы в дважды резонансных системах. Экспериментальные данные, представленные на рис. 12.А. З подтверждают резо­нансную природу этого нелинейного оптического эффекта.

CD

S 5 CD Z Ф 2 Z 0 В 0 о о

§ 0.15 О С 0

О 5 0.05

I Го

Рис. 12.А. З. Процессы поглощения и генерации второй гармоники излучения в дваж­ды резонансных квантовых ямах (Из Е. Rosencher and P. Bois, Phys. Rev., В 44, 11 315 (1991) и P. BOucaud, et al Appl. Phys. Lett. 57, 215 (1990)).