Оптоэлектроника

Кристаллические структуры, блоховские функции и зона Бриллюэна

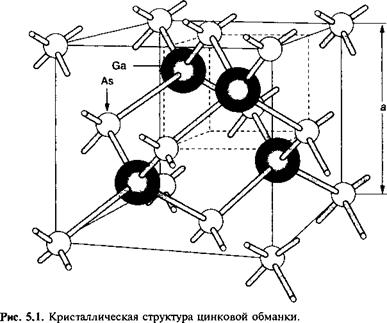
Наиболее устойчивая структура материи при температуре абсолютного нуля реали­зуется в виде периодического расположения атома в кристаллической структуре. Число возможных кристаллических структур огромно и является проблемой осо­бой науки как таковой, а именно — кристаллографии. Кристаллическая структура характеризуется периодическим повторением (до бесконечности или практически до бесконечности) от точки к точке (при этом возникающая конфигурация называ­ется кристаллической решеткой), базисом которой являются один или несколько атомов. Термин «моноатомная решетка» используется для описания решетки, воз­никающей в том случае, когда для заполнения решетки необходим базис, включа­ющий единственный тип атомов. Наиболее типичным типом структуры решетки для кристаллов элементарных полупроводников (Si, Ge, С) является структура ал­маза. В случае бинарных полупроводников, таких как GaAs, наиболее типичной является структура цинковой обманки, показанная на рис. 5.1.

В первую очередь, следует отметить тот факт, что кристаллическая решетка в этом слу­чае может быть представлена линейной комбинацией трех базисных векторов а,, а2 и а3, т. е. кристаллические узлы распределены по точкам г таким образом, что:

Г = я, а, + «2а2 + «3а3

Где п. соответствует произвольным целым числам. Гамильтониан, описывающий взаимодействие между электронами и атомами в кристалле, является чрезвычайно сложным, и он должен учитывать взаимодействие между всеми электронами, дви­жения ядер и т. д. Таким образом первая цель физики твердого тела заключается в том, чтобы показать, что многие из этих взаимодействий по кристаллу могут быть учтены с использованием эффективного потенциала 1/(г) таким образом, что га­мильтониан, используемый для описания электрона в кристалле, принимает вид:

Или иначе:

TOC o "1-5" h z Яспя=£-+К(г) (5.3)

Где К(г) обладает периодичностью кристалла:

Кг + г.)=К(г) (5.4)

С учетом условия периодичности кристалла (5.4) периодический потенциал может быть разложен в ряд Фурье:

К(г)= ^K(G)e-iGr (5.5)

GeRL

Где точки G (OG = G) распределены в пространстве обратной решетки (RL), пере­крываемом единичными векторами:

А, = 2л Й2><аз ; А2 = 2м 83X81 ; К, = 2л а'ха? (5.6)

а, а2ха3 а2 а3ха, а3а, ха2

Конструирование обратных решеток кристаллических структур лежит в облас­ти почитаемой нами геометрии. Рис. 5.2 иллюстрирует одномерную моноатомную решетку (а), а также соответствующую обратную решетку (б).

Напоминаем, что в вакууме, где #= р2/2/я, стационарные волновые функции к сво­бодных электронов представляются волновыми векторами и могут быть записаны в виде ехр (—ik • г). Легко может быть показано, что решениями уравнения Шредингера Crystal ^ = ^^(г) являются функции Блоха с индексами в виде волновых векторов к:

Т(г) = «к(г)е_1кг (5.7)

Функции Блоха—Фуке

Где функции ^(г) обладают периодичностью кристалла:

Кристаллическая решетка

Первая зона Бриллюэна

Рис. 5.2. Кристаллическая (а) и связанная с ней обратная (б) решетки. Вектор трансляции для обратной решетки есть вектор А, расположенный при 2п/а. Два перпендику­ляра, проведенные из середины ОА и - ОА определяют первую зону Бриллюэна обратной решетки.

Действительная (или мнимая) часть функции Блоха—Фуке показана на рис. 5.3. Отметим общую форму этих функций, характеризуемую быстро изменяющимися атомными волновыми компонентами, медленно модулируемыми огибающей функци­ей вида ехр(—ik • г). Именно эта модуляция переносится по кристаллу и лежит в основе феномена эффективной массы, рассматриваемого в дальнейшем.

Как обычно при трактовке бесконечной среды, волновые векторы к из сообра­жений удобства представляются псевдо-квантованными (смотрите Дополнение 1 А). Этого можно добиться, вводя бесконечные потенциальные барьеры вдоль шести плоско­стей, определяемых:

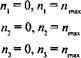(5.9)

В этом случае псевдо-квантование привело бы к положительным дискретным волновым векторам к. Волновые функции Блоха были бы таким образом стацио­нарными, так как они были бы результатом наложения волн, распространяющихся вперед и назад в обоих направлениях между ограничивающими поверхностями. Традиционным в физике твердого тела является также и использование другой процедуры: цикличных граничных условий Борна—фон Кармана. С этой целью предпо­ложим, что при всех значениях 1и. = №.(/ = 1, 2, 3) кристалл идентично воспроизво­дит себя в пределах каждого из этих «ящиков», т. е., иначе говоря, все пространство внутри кристалла полностью заполнено прилегающими друг к другу ящиками с размерами Ь{х Ь2х Ьу Циклические граничные условия Борна—фон Кармана тре­буют, чтобы волновая функция Ч'(г) была той же самой в каждом из этих ящиков, т. е. чтобы у (г + + л2Ь2 + л3Ь3) = Ч'(г) Волновые векторы к, в этом случае

Принадлежат обратному пространству, описываемому точками:

Где п{, я2, пъ в данном случае представляют собой положительные или отрицатель­ные целые числа. Понятно, что величина N может быть сделана сколь угодно боль­шой таким образом, чтобы сделать незаметным какое-либо влияние процедуры псевдо - квантования.

В совокупности с граничными условиями Борна—фон Кармена уравнение Шре - дингера (5.3) имеет решения в виде функций Блоха (5.7) или ^(г) Для каждого к имеется целый набор решений, собственные энергии которых мы обозначаем как £т(к), при этом т являются целыми. Мы можем представить, что эти наборы реше­ний образуют непрерывные зоны в том смысле, что при к',близких к к, ^(к') будут также близки к Ет(к). Вследствие этого т называют индексом зоны.

Мы должны также понимать, что в большем масштабе собственные состояния блоховского вида (5.7), соответствующие зоне т, с вектором обратного простран­ства в могут быть также записаны в виде:

(5.11)

Что опять имеет блоховский вид, поскольку енс г является периодической функци­ей кристаллической решетки. Таким образом, это выражение идентично одному из решений уравнения Шредингера для волнового вектора к — в. Применительно к собственным энергиям мы получаем:

(5.12)

Следовательно, энергетические зоны периодичны по т при этом период определя­ется обратной решеткой.

Следующим следствием того, что у/^ к _ с (г) идентична тому же самому решению у/т к_с(г), является то, что для представления всех решений у нас нет необходимо­сти в обратном пространстве.

Принято (как это объясняется в дополнении 5.А) ограничивать целые значения п в (5.10) интервалом — N/2 < п. < N/2 (т. е. п{ 2 3= 0, ±1, ±2,..., ±N/2). Таким образом, волновые векторы, принадлежащие той же самой зоне, определяются выражениями:

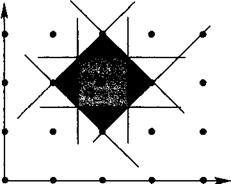
Эта зона задается набором перпендикулярно пересекающихся плоскостей, ко­торые пересекают посередине трансляционные векторы обратной решетки (RL) (соединяющие ближайшие соседние точки RL). Область пространства в RL, опре­деленную таким образом, называют зоной Бриллюэна. На рис. 5.2 представлена первая зоны Бриллюэна для одномерной структуры. Рис. 5.4а и 5.4б показывают первую зону Бриллюэна для двумерной квадратной решетки, а также для трехмер­ной структуры цинковой обманки. Наиболее важные точки (и соответствующие направления) в последнем случае имеют общепринятые обозначения.

В ряде случаев при отсчете зон более удобно использовать периодичность, свя­зывая собственную энергию с каждой точкой обратного пространства. Примером тому является модель почти свободных электронов, исследованная в дополнении 5.А. Для того, чтобы возвратиться к стандартной зонной структуре первой зоны Бриллюэна в таком представлении решений, необходимо осуществить трансляцию зоны (подобно уравнению (5.12)) на вектор обратной решетки G, приводящую к тому, что вектор k—G будет лежать в первой зоне Бриллюэна. Такая процедура, обычно называемая приведением зон, иллюстрируется рис. 5.А.2.

Одной из главных проблем физики твердого тела является решение уравнения Шредингера, получаемого подстановкой (5.11) в (5.12). Обычно это осуществляет­ся с использованием достаточно трудоемких численных методов, что позволяет по­лучить зависимость Јm(k), связывающую энергию электронов в структуре с соот-

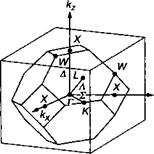Г 1 Первая зона Бриллюэна

1Н1 Вторая зона Бриллюэна а б

Рис. 5.4. Первая и вторая зоны Бриллюэна двумерной квадратной решетки (а) и пер­вая зона Бриллюэна трехмерной структуры цинковой обманки (б). В после­днем случае приведены общепринятые обозначения для наиболее важных то­чек симметрии.

Ветствующими значениями волнового вектора к в первой зоне Бриллюэна для за­данного индекса т. Совокупность получаемых кривых Ет(к) определяет зонную струк­туру материала. На время удовлетворимся суммированием основных аспектов этой важной области физики твердого тела.