Колебательный подход к волноводам
Вспомним, что электрическое поле электромагнитной волны в нейтральной среде а = 0 и р = 0) с коэффициентом преломления п(т) является решением волнового уравнения, следующего из уравнений Максвелла (смотрите Главу 2):
2
УЕ(г, 0 - ^Мг^ЕО-, /) = 0 (9.9)
Предположим, что волна имеет радиальную частоту со, т. е. что поле Е определяется
Формулой:
Е(г, /) = Яе[Е(г)е-'] (9.10)
Это выражение приводит к уравнению Гельмгольца для амплитуды Е(г):
У2Е(г) + К2п2(т)Щт) = 0 (9.11)
Здесь к есть модуль волнового вектора к, связанный с со вакуумным дисперсионным соотношением к = со/с. Рассмотрим частный случай с волной, распространяющейся вдоль оси 01 (рис. 9.3).

|
Рис. 9.3. Геометрия планарного л2 Волновода. |
![]() Х
Х
В этом случае мы можем представить поле в виде Е(т, /) = Е(х, у)с при этом уравнение (9.11) может быть записано следующим образом:
|
(9.12) |
![]() -|^Т +у)+[к2п2(т)~ Рг^(х, у) = О
-|^Т +у)+[к2п2(т)~ Рг^(х, у) = О
Заметим, что условие одинаковости константы распространения Р в среде 1 и среде 2 соответствует условию самосогласования, приведенному в разделе 9.2. Наконец, предположим, что волна не изменяется вдоль направления у, т. е. что д/ду = 0. В этом случае возможно разделение уравнения (9.12) на три уравнения:
-^-ТЕ(х)+ (к2п2 -/32)е(х)= 0, для х > 0 дх
|
(9.13) |
![]()
|
Дх2 _Э^ Дх: |
![]() Е(х)+ (к2п2 - /32)е(х)= 0, для - сі < х < 0 Е(х)+ (к2пI - р1 )е(х) = 0, для х <-с!
Е(х)+ (к2п2 - /32)е(х)= 0, для - сі < х < 0 Е(х)+ (к2пI - р1 )е(х) = 0, для х <-с!
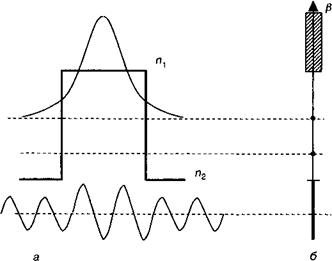
Напомним, что я, > п2. На этой стадии рассмотрения мы можем проанализировать различные решения (9.13), исследуя влияние различных значений кп. и /3(смотрите рисунок 9.4).
Если /3> кпх, то к2п} — /^является отрицательной величиной независимо от величины х, решения (9.13) экспоненциально расходятся, что соответствует нефизическому решению.
Если кп{ > Р > кп2, то амплитуда Е (х) в волноводе является синусоидальной функцией, а за пределами волновода — экспоненциально затухающей функцией. Этот случай соответствует волноводным модам, которые мы определим позже, введя соответствующие граничные условия.
Наконец, если р < кп2, то решения будут синусоидальными повсюду и волна будет выходить из волновода. Такая ситуация соответствует случаю утекающих мод, когда падающий световой пучок входит в волновод таким образом, что эффективный угол в волноводе превышает критический угол полного внутреннего отражения. На время оставим эти утекающие моды, которые в действительности могут
|
|
|
Запрещенная Область |
|
Кп* |
|
Волноводные Моды |
|
/сЛ 2 |
|
Континиум |
|
Рис. 9.4. Различные электромагнитные режимы в волноводе аналогичны различным электронным состояниям в квантовой яме: рисунок (а) показывает пространственное изменение коэффициента преломления л(г), а также изменение амплитуды поля; рисунок (б) иллюстрирует разрешенные значения константы распространения Д |
|
|
Быть использованы в ряде интересных практических применениях. Теперь же более детально исследуем решения (9.12) для ТЕ - и ТМ-мод.
Поперечные электрические (ТЕ) волны
В рассматриваемом случае электрическое поле ориентировано вдоль оси Оу. Обозначим его амплитуду как Е(х), т. е.£(*> = (х)еКл"-/%)]. При этом магнитное поле ^опреде
Ляется уравнением Ленца—Максвелла (V х Е = —<?В/<?/), которое дает:
Со дх
Из уравнений Максвелла мы знаем, что электрическое поле Е(х) и магнитное поле В^х) (т. е. первая производная Е) непрерывны на обеих границах раздела при х = 0 и х=—& Отметим, что эти уравнения распространения, полученные из (9.12), вместе с граничными условиями формально идентичны уравнениям Шредингера, которые приводят к квантованию электронных энергетических состояний в квантовых ямах, описываемых потенциалом У{х) (раздел 1.4). Указанное соответствие имеет вид:
Со2с2п(г)2 <н>--^г-К(г)
/г
Е(т) у/(г)
Рисунок 9.4 иллюстрирует эту аналогию квантовой ямы и волновода. Утекающие моды соответствуют континууму несвязанных состояний над квантовой ямой тогда, как волноводные моды концептуально эквивалентны связанным состояниям в квантовой яме. Отметим к тому же, что форма (глубина) ямы зависит от частоты со, как это показано в соотношениях соответствия, приведенных выше.
Граничные условия для (9.13) имеют вид:
ЕАх) непрерывна при х = 0 и х = - с!
' (9.15)
— Е Ах) непрерывна при х = 0 и х =
Дх
При этом процедура получения решений (9.13) аналогична случаю квантовой ямы (раздел
1.4) . Желая получить пространственную зависимость амплитуды волны, предположим:
А ехр (- кх ) для лс > О
|
Е„ = |
![]() В со8(ш:)+ С эт (ах), для - с/ <х < 0 (9.16)
В со8(ш:)+ С эт (ах), для - с/ <х < 0 (9.16)
О ехр [л:(х + г/)] для х < - с1
Здесь: к — константа оптического ослабления вне волновода. Этот параметр эквивалентен длине туннельного ослабления в квантовой механике. Начнем с введения условия самосо- гласования, представленного в (9.13), что дает:
Р2 +а2 = п2к2 р2 - к2 = п^к2 к = со/с
|
---------- ► Р = п^к СОБ в |
|
ПЛ |
|
|
|
|
|
|
|
Нам остается записать граничные условия (9.15):
• при х = 0:
|
А = В
|
|
|
А$т(рссі)- ксо$(рссі)= к со$(си/)+ — ^т(асі)
Это последнее условие дает параметры волноводной волны:
І%(асі)= Ка
А - к
2 2 2 :
|
(9.18) |
![]() Р + а = п{ к
Р + а = п{ к
2 2 2 2 Р - к = гц к
К = со / с
Система уравнений, определяющих ТЕ-моды в симметричном волноводе
Таким образом, задача заключается в нахождении при заданной радиальной частоте со и толщине с1 константы распространения Д которая удовлетворяет одновременно всем условиям (9.18) и приводит к точному уравнению относительно Д полностью эквивалентному (9.5). Этот подход может быть обобщен на случай волновода произвольной формы. Ниже мы приводим программу МАТНЕМАТ1СА, которая может быть использована для получения решений для асимметричного волновода.
Пример-----------------------------------------------------------------------------------------------------------
Обобщение (9.18) на случай асимметричного волновода немедленно приводит к:
|
К7 + к,
2 2 2 2 Р + а = /1, к 2 2 2 2 Р - К2 = п2 к 2 2 2 2 Р - к3 = п3 К |
Здесь использована обычная система обозначений. Рассмотрим волновод с сердцевиной на основе слоя СаАБ толщиной 0,3 мкм (я, = 3,3), заключенного с одной стороны между ограничивающим слоем А1Аб (п2 = 2,7) и воздухом (я3 = 1). В расчетах будем пренебрегать собственной дисперсией в этих средах.
1_атЬс1а=0.9;1=.3;Ве1=.;
N3=1 ;п1=3.3;п2=2.7;
К=2*М[РП/1_атЬс1а;
Ве«=ВеП;
М=8дП[(пГ2*кГ2-Ве«~2)];
Ц=ЗцП[(-пЗ~2*кГ+ВеП''2)]‘,
Р1=8дИ[(-п2~2*кГ2+Ве«~2)];
ЦВеЪ_ ]:Тап[М]-(д1+р1)/(М-р1*д1/М);
РкЛИВеЧЛВеЪЮ. бО}];
8о1=НпсШооЦТ[Ве1]= =0,{Ве^21}];
Neff=Bett*Lambda/(2*N[Pi])/.sol
При этом получаем, что константа распространения составляет 21,3 мкм-1, а эффективный коэффициент преломления ясд. =3,1267.
Представляется интересным для частного случая симметричного волновода установить связь между геометрическим подходом раздела 9.1 и колебательным подходом, используемым в настоящем разделе. Для этого достаточно заметить, что вектор распространения в волноводе есть (0, ±п1ксоь6т, п^кьхп6т). Затем, учитывая (9.18), получаем
|
(9.19) |
![]() Рт = п}к сое 9т ат = пхк сое 0т
Рт = п}к сое 9т ат = пхк сое 0т
|
|
Эквивалентность геометрического и колебательного подходов
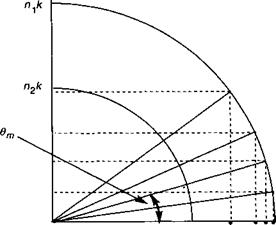
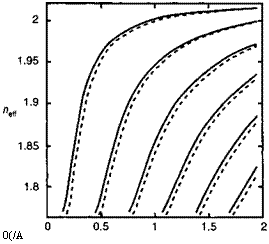
Эти соотношения представляют собой ничто другое как (9.5), и они хорошо поддаются графической интерпретации, как это показано на рис. 9.6. Мы видим, что нулевой порядок (минимальное значение 0т) приводит к максимальному коэффициенту ослабления кт, т. е. к максимально локализованной моде.
Теперь нам остается нормировать амплитуду электромагнитной волны в волноводе, т. е. найти величину константы А в (9.16). В ее определении имеется определенная степень произвола, так как мы не уточнили размеры поперечной протяженности Оу. Обычный в таких случаях подход заключается в таком выборе А, чтобы нормированное поле Еу соответствовало мощности в 1 Вт на длине волновода в 1 м (вдоль Оу). В этом случае условие нормировки может быть записано в виде:
|
(9.20) |
![]()
|
0(/А |
|
Рис. 9.6. Дисперсионные кривые для волновода в недесперсионной среде с /7, = 2, п2 = 1,5 и п3 = 1. ТЕ (ТМ)-моды показаны сплошными (пунктирными) линиями. |
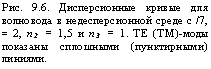 5 = — І"Е х Всіх = - —І"ЕВхйх = ГГ(л:)] сЬс = р0 Мо • 2»„ J 2оша З1_ .
5 = — І"Е х Всіх = - —І"ЕВхйх = ГГ(л:)] сЬс = р0 Мо • 2»„ J 2оша З1_ .
В этом последнем уравнении мы использовали соотношение (9.14) (горизонтальная черта показывает, что данная величина усредняется по времени; р0 есть единичная нормированная мощность, соответствующая 1 Вт/м, а т есть индекс ТЕ - моды в волноводе). Мы рекомендуем использовать р0 для того, чтобы уравнения были однородными, что имеет первостепенную важность, например, при рассмотрении эффектов нелинейной оптики (смотрите дополнение 9. В)! При использовании выражения (9.16) для полевых и граничных условий уравнение (9.20) дает:
-1І/2
SHAPE \* MERGEFORMAT ![]()
|
То |
![]()
|
(9.21) |
![]() Лт = 2 ап
Лт = 2 ап
|
К |
![]() (І + -
(І + -
В качестве последнего замечания отметим, что поскольку функции Е™(х) являются решениями линейных дифференциальных уравнений (т. е. собственными векторами дифференциального оператора (9.12)), они взаимно ортогональны. Говоря более точно, с учетом условия нормировки (9.20) функции Ет(х) удовлетворяют
Уравнению:
|
(9.22) |
![]() Е;(х)Е"у(х)іх = ^^6т
Е;(х)Е"у(х)іх = ^^6т
Г* т
Таким образом, если волновод является абсолютно ограничивающим (т. е. если пх/пг —>°°) моды могут быть записаны в виде:
(9.23 а)
Ттих
Мода т в абсолютно ограничивающем волноводе
Давайте специально выпишем для этого случая несколько очень полезных аппроксимаций для коэффициентов а и к (т =1):
( 2 2 V/2 2/Г
*вЦ2-/!22) ------------
Поперечные магнитные (ТМ) волны
В рассматриваемом случае компоненты электромагнитного поля могут быть разделены, при этом поперечная магнитная компонента может быть записана в виде:
Ву(х, /)= ] (9.24)
В то же время электрическое поле Е, определяемое V х В = /(п. с)2дЕ/дг, может быть записано в виде:
Ех(х, г, г)=Щ-В,(х, г, О
П, СО
(9.25)
£г(х, г, /)= --^-^-В (х, I, О Щ О) ох
Здесь п. есть коэффициент оптического преломления среды /. Собственные ТМ-моды в волноводе получаются при наложении условий непрерывности для полевых компонент В и Е1 на обеих границах раздела (это мы оставляем читателю в качестве упражнения). Это приводит к следующему результату:
А~ -£пКУ Р2 + а2 = агг к
’ V (9-26)
Р~ - к~ - п;к~
К = со/с и еп =
Система уравнений, определяющих ТМ-моды в симметричном волноводе
Для каждой комбинации величин частоты со и толщины с1 мы получаем многочисленные разрешенные значения для константы распространения Р различных мод. Общепринятое представление различных мод в волноводе заключается в отображении дисперсионной кривой яс{Г(/10), где яе{Г есть эффективный коэффициент оптического преломления для волновода, определяемый как яе{Г = Рс/со.
Рисунок 9.7 показывает дисперсионную кривую для теоретического волновода с я, = 2, п2 = 1,5 и А13 = 1 в функции *//Л0. Как явно видно из этого рисунка, имеется несколько возможных решений, т. е. возможны несколько решений, при этом волноводы по своей природе являются, таким образом, многомодовыми. Позже мы увидим, что для большинства применений предпочтительными являются одномодовые волноводы. В этом случае одномодовое распространение гарантируется при удовлетворении условия (9.8), т. е. когда отношение £//Л0 меньше N^2. Из рисунка 9.7 мы также можем заключить, что волновод естественно вводит дисперсию, т. к. всегда существует разброс между максимальными значениями пх и п2. Этот фактор обычно называется модовой дисперсией волновода. Эта компонента дисперсии дает свой вклад в естественную дисперсию, определяемую материалами, образующими волновод.
|
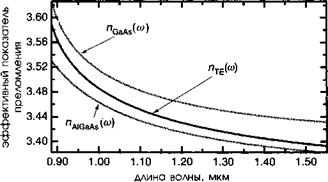
Рис. 9.7. Дисперсия в волноводе, содержащем слой сердцевины толщиной 0,5 мкм, заключенный между двумя слоями Al0 ,Ga09As толщиной 1,0 мкм. Возникающая естественным образом дисперсия из образующих волновод материалов дает свой вклад в дисперсию из-за геометрии волновода.(С разрешения A. Fiore. LCR. THALES.). |
|
Рисунок 9.8 демонстрирует результат полного расчета для системы AlGaAs с использованием дисперсионных соотношений Афромовича, приведенных в дополнении 7. Б. Мы увидим, что эта дисперсия приводит к отрицательным эффектам в нелинейно-оптических волноводах.
|
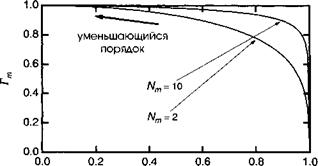
Sin вт /sin в с
Рис. 9.8. Зависимость коэффициента ограничения оптического волновода от sin 0J /sin вс. Волноводные моды с малыми индексами (малая величина sin вт) обеспечивают лучшее оптическое ограничение.