Коэффициент бимолекулярной рекомбинации
Уравнение (7.44), которое было описано в последнем разделе, выражает распределение скорости переходов (см-3 с-1 Дж-1) в функции энергии фотонов для двух неравновесных распределений носителей с использованием соответствующих квазиуровней Ферми. Теперь найдем полную скорость рекомбинации для фотонов всех энергий, т. е. используем интегрирование распределения (7.44) по Иу.
Я5ро„ = — 'р1(Ьу )/с [Ес (А V )] {1 - /„ [£•,, (А V )] }с1 А V (7.55)
Т п Г
|
Где произведение двух распределений Ферми—Дирака дается (7.51) или: Е(£>,-£л)/*Г |
|
-hv/kT |
|
(7.56) |
|
Dhv |
|
R = Spon |
|
-jPj(hv)eh |
Теперь используем выражение для комбинированной плотности состояний (7.19в) и получим:
|
1 2 п2 |
|
|
|
|
|
І f |
![]() (7.57)
(7.57)
|
In2 |
J n
Это уравнение может быть сильно упрощено с учетом того, что в приведенном выше уравнении (7.57) мы узнаем эффективную плотность состояний, приведенную в (5.42) и (5.43):
|
КТ |
![]() 3/2
3/2
где мы заменили эффективную массу в зоне проводимости на приведенную эффективную массу тг, при этом:
_1_ дт Аск-Е>,-Е*)/кТ
Коп - Nj. q (7.59)
Т в
Ь Я
С учетом выражений (5.42)—(5.45) для эффективной плотности состояний в двух зонах, а также концентрации носителей в функции энергии Ферми, уравнение (7.59) принимает вид:
1 N.
/?=-------- J—np-------------------------------------- (7.60)
Spon тR NNV У V ;
Это последнее уравнение лучше известно в виде:
V, = Впр (7.61)
ХЗ/2
|
(7.62) |
![]()
|
) |
![]() Г* NeN, trNc
Г* NeN, trNc
Скорость излучательной рекомбинации (см-3 с-1) и коэффициент излучательной бимолекулярной рекомбинации (см-3 с~1)
Где В есть коэффициент бимолекулярной рекомбинации. В таблице 7.2 представлены экспериментально определенные значения коэффициента В для ряда наиболее важных полупроводниковых соединений III—V.
|
Табл. 7.2. Коэффициенты бимолекулярной рекомбинации для различных прямозонных полупроводников (поданным V. P. Varshni, Phys. Stat. Sol. 19, 459 (1967))
|
Пример---------------------------------------------------------------------------------------------------------------------------------------------------
Для ОгМ эффективная платность состояний в зоне проводимости составляет ТУ = 4,3 х Ю17 см-3 (раздел 5.6.1) и излучательное время жизни тк равно 7 х 10-10 с. Приведенная масса есть 1/(1/0,067) + (1/0,50) = 0,059. Коэффициент бимолекулярной рекомбинации В в этом случае составляет 1/(7 х Ю-10 с х 4,3 х 1017 см-3) х (0,059/0,50)3/2 или 1,34 х 10-10 см3 с-1, что достаточно близко к экспериментальной величине ~10-10 см3 с-1.
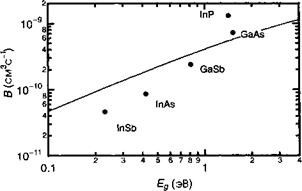
В более общем случае коэффициент бимолекулярной рекомбинации может быть рассчитан с использованием выражения для ТУ в (7.62) и выражений для эффективных масс тг и /яу, приведенных в (5.В. 19) и (5.В.27) в рамках теории Кейна. Принимая энергию Кейна постоянной в соединениях III—V и равной -20 эВ мы, таким образом, можем вывести величину коэффициента В в функции ширины запрещенной зоны соединений III—V. На рис. 7.5 приведено сравнение результатов этой простой теории с экспериментальными данными, приведенными в табл. 7.2.
|
Рис. 7.5. Коэффициенты бимолеклярной рекомбинации для различных полупроводников III—V. Сплошная линия представляет собой обобщенную зависимость, полученную с использованием (7.62) в предположении о том, что энергия Кейна постоянна и составляет 20 эВ для всех полупроводников. Точки на рисунке соответствуют экспериментально полученным данным. |
Мы можем сделать заключение о том, что соответствие в данном случае вполне удовлетворительно. Таким образом, данная теория обладает достаточным потенциалом для прогнозирования и может быть еще более улучшена за счет учета дополнительных вкладов от спин-орбитально отщепленной зоны и т. д.
Выражение (7.61) представляет собой закон действующих масс: электроны и дырки рекомбинируют индивидуально друг с другом, при этом скорость рекомбинации определенного типа носителей, очевидно, пропорциональна концентрации носителей другого типа. Предположим, что обычно встречающаяся ситуация состоит в слабом смещении системы из состояния равновесия. В этом случае равновесные концентрации носителей л0 и р0 связаны друг с другом законом действующих масс п^)0 = я.2, где п. есть собственная концентрация носителей (5.49). В этом случае неравновесные концентрации носителей определяются соотношениями:
П = яп + Ап
0 (7.63)
Р=Р0 + АР
Где предполагается, что Ап и Ар малы по сравнению с концентрацией основных
Носителей, при этом (для обеспечения нейтральности заряда) Ап = Ар. В этом слу
Чае дополнительная скорость рекомбинации составляет:
= В(пр ~п0р0)= В(п0 + р0)&п (7.64)
При этом скорость излучательной рекомбинации неравновесных носителей равна:
В - Ап
Га“ (7.65)
( 1 1
В(п0+р0) ВИаор
Время излучательной рекомбинации в полупроводнике
Где А^ор есть уровень легирования полупроводника. Время излучательной рекомбинации может быть также записано в виде:
Таким образом, время излучательной рекомбинации достаточно близко к спон
Танному времени жизни тк, т. е составляет величину порядка наносекунд. К сожалению, эти два понятия часто путают.
Пример--------------------------------------------------------------------------------------------------------------
Для кристалла ваАз, легированного до концентрации 1017 см-3, эффективная плотность состояний в зоне проводимости составляет ТУ = 4,3 х 1017 см-3 (раздел 5.6.1), время спонтанной эмиссии тк равно 7 х 10-10 с и приведенная эффективная масса равна 1/(1/0,067) + (1/0,50) = 0,059. В этом случае излучательное время жизни составляет:
^ = 7 х 10"10 с х (4,3 х 1017 см_3/1017 см"3) х (0,5/0,059)3/2 или = 5 не