Оптоэлектроника

Излучение черного тела

Именно исследование спектрального распределения света, излучаемого нагретыми объектами, позволило Планку ввести понятие дискретных квантов энергии, на ос­новании которого в дальнейшем Эйнштейн разработал концепцию фотона. Мы можем определить черное тело как соответствующий резонатор, в котором электро­магнитные моды находятся в термодинамическом равновесии со стенками при тем­пературе Т. В этом случае излучение поглощается и переизлучается внутри резона­тора без обмена с внешней средой. Без введения фотона (т. е. без постулата квантов минимальной энергии) Рэлеем и Джинсом было установлено, что энергия, содер­жащаяся внутри такого резонатора, стремится к бесконечности. Этот знаменитый теоретический «тупик» был назван «ультрафиолетовой катастрофой». Здесь мы не будем воспроизводить эти расчеты. Отметим лишь значение, которое оказала эта проблема на ранний период развития квантовой механики.

Рассмотрим резонатор с объемом Ь3 и попробуем найти плотность оптических мод для каждой частоты у(т. е. число мод, содержащихся в частотном интервале (IV):

(2.79)

Внутри резонатора волны состоят из линейных комбинаций мод, описываемых выражением (е1кг ± е_1кг). Требование в качестве граничных условий обращения в ноль электромагнитных полей на стенках резонатора накладывает условия на вол­новые векторы к = (кх, ку, ку.

, К I К,71

К = £ и,; К = - пу кг = - пг (2.80)

Где пх, пу, — положительные целые числа. Таким образом, мы можем связать с

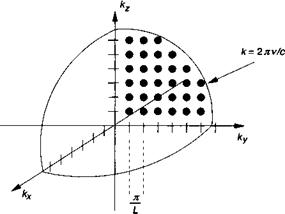
Каждой модой (кх, к, к) объемный элемент йкх, йк, йк в обратном пространстве (рис. 2.2). ' '

Число мод, содержащихся в интервале между к и к + йк, составляет одну восьмую (пх, пу, пг положительны!) сферического слоя объемом 4тгк2с1к9 умноженную на два с учетом двух возможных поляризаций каждого волнового вектора. Следовательно имеется:

1}к2

<1ЛГ=^Ц-<1 к (2.81)

Л

Электромагнитных мод. Используя дисперсионное соотношение для излучения, рас­пространяющегося в вакууме:

У = ^-к (2.82)

2 71

Получаем выражение для плотности мод черного тела рт на единицу частоты и объема:

= ^ (2.83)

Приведенное выше уравнение дает плотность электромагнитных (ЭМ) мод в частотном интервале от удо у+ ёк Теперь ответим на вопрос, какова же вероят­ность того, что этот частотный диапазон (V, V + ёу) в действительности заполнен колебательными модами в условиях теплового равновесия?

Вероятность нахождения ЭМ-осциллятора в энергетическом состоянии Еп да­ется законом Больцмана:

Рп ос е-Еп/кт (2.84)

Где к — постоянная Больцмана (к = 1,38 х 10"23 Дж/К или 8,62 х 10“5 эВ/К) и символ

Ос в (2.84) обозначает пропорциональность. Поскольку Еп = ку(п - I - 1/2), эта вероят­

Ность дается выражением:

Р. (2.85)

Где к — коэффициент пропорциональности, определяемый условием нормировки:

Х^=кХ(е'(^МГ))"=кТТ^п=1 {2Ма)

П=0 п=0 1 С

Так, что:

Рп = (| _ (2.866)

Теперь представляет интерес определить среднее число пу фотонов с частотой V в резонаторе при температуре Т:

(2.88)

Аналогичный расчет (оставляемый нами в качестве упражнения) позволяет найти дисперсию сг числа фотонов:

°п =[4] Я + К~ (2-89)

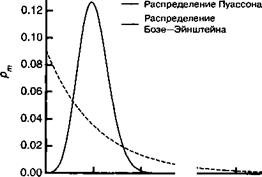
Сравнивая приведенное выше выражение с (2.70), полученным в подходе Гла­убера, приходим к выводу о том, что распределение Бозе—Эйнштейна намного шире распределения Пуассона. Рис. 2.3 иллюстрирует это распределение для сред­него числа фотонов в резонаторе, равного десяти (п = 10). Флуктуации числа фото­нов в излучении черного тела намного больше, чем в когерентном состоянии, что

0.14
40	50
Рис. 2.3. Сравнение распределений Пуассона и Бозе—Эйнштейна для среднего числа фотонов в резонаторе, равного десяти.

Впрочем и не удивительно. Теперь мы уже можем найти спектральное распределе­ние излучения черного тела при температуре Т.

Средняя энергия, распределенная в моде с частотой V, дается средним числом фотонов в этой моде, умноженным на энергию фотонов:

В результате плотность энергии ре( у) излучения в резонаторе в единичном час­тотном и объемном интервале (в Дж с /м3) дается произведением (2.83) и (2.90):

(2.91)

Закон Планка (спектр излучения черного тела)

Эта формула для спектра излучения черного тела была открыта Планком в 1900 году. В дополнении 2. Б мы исследуем более детально особенности, связанные с тепловым излучением, а также рассмотрим использование спектров излучения черного тела в тепловидении.