Формализм огибающей функции
Волновые функции электрона в гетеропереходе можно описать с использованием формализма огибающей функции. Эта аппроксимация формально идентична той, которая используется для описания распространения электромагнитной волны в неоднородной среде, как например, в случае волновода в (9.27) или в нелинейной оптике, как в (12.21). Данный раздел является достаточно проблемным и читатель может просто принять (8.17) на веру и перейти к другому разделу.
Теперь мы выведем аппроксимацию огибающей функции для полупроводника, обладающего периодическим потенциалом К (г), отражающим кристаллическую периодичность решетки. Обсудим простой случай электрона в зоне проводимости гетероструктуры — более сложная проблема, связанная с вырождением валентной зоны будет оставлена до дополнения 8.Г.
|
Ч« ГГГГГГГГ |
![]()
|
<Mnf |
![]()
|
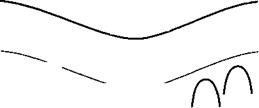
Рис. 8.3. Потенциал, действующий на электрон, состоит из кристаллического потенциала и внешенго потенциала, представленного изогнутой линией. |
![]()
|
Т |
![]() Рассмотрим потенциал К(г), медленно изменяющийся по г, как это показано на рис. 8.3. Гамильтониан электрона, задаваемый этой комбинацией потенциалов, в этом случае может быть записан в виде:
Рассмотрим потенциал К(г), медленно изменяющийся по г, как это показано на рис. 8.3. Гамильтониан электрона, задаваемый этой комбинацией потенциалов, в этом случае может быть записан в виде:
|
(8.1) |
![]() H=^—+Vc( г) + Н(г)
H=^—+Vc( г) + Н(г)
2 пи
Для К(г) = 0 решения уравнения Шредингера Ну/ = Еу/ представляют собой блоховские функции |п, к) (смотрите главу 5):
|
1 |
|
^Як(г) = |
|
|
|
|
Где О, есть объем кристалла, п — индекс зоны, а ип к(г) обладает периодичностью решетки. Соответствующая энергия есть еп к.
При Уф О разложим решения уравнения Шредингера (8.1) по набору волновых функций базиса в виде блоховских функций:
|
(8.3) |
![]() !/(г) = ^^ц„keikrM„k(r)
!/(г) = ^^ц„keikrM„k(r)
При этом должно удовлетворяться уравнение:
|
(8.4) |
|
+ К(г) |
|
2 т( |
|
Јa„keik4k(r) + 5V(r)a„keik4k(r) = E^a^'u^r) Лк як як |
Поскольку волновая функция Блоха является решением задачи для «кристалла с нулевым потенциалом», это последнее выражение может быть переписано в виде:
Х£Ае‘кГ^<г) + ХК(г)а"'‘еАГм"к(г) = я£«*е‘Ч*(г) (8.5)
Лк пк лк
|
(8.6) |
![]() После этого спроецируем это выражение на волну |7УК) = £2_1/2еікг и А^К. В этом случае, используя ортогональность блоховских волновых функций, получаем эквивалентное выражение для уравнения Шредингера:
После этого спроецируем это выражение на волну |7УК) = £2_1/2еікг и А^К. В этом случае, используя ортогональность блоховских волновых функций, получаем эквивалентное выражение для уравнения Шредингера:
;(r)K(r)eikrM„k(r)dr = (Е - em)a„
Вплоть до настоящего момента мы не допустили никаких изъянов в нашем выводе. Таким образом, вполне разумным представляется подумать над тем, какие аппроксимации необходимы для упрощения приведенного выше выражения. В связи с этим заметим, что если К(г) является постоянной величиной, то левая часть будет
представлять Фурье-образ величины илк(г)ммс(г) и она будет зависеть только от кристалла.
Тот факт, что К(г) изменяется очень медленно, означает, что Фурье-образ, определяемый выражением:
(8.7)
|
|
Равен нулю за исключением значений ч, очень малых по сравнению с радиусом зоны Брил- люэна. При подстановке (8.7) в (8.6) возникает следующий член:
|
|
(8.8)
Этот член будет практически равен нулю для постоянной величины V Поскольку функции иж и ипк являются периодическими, мы можем положить, что г = К. + г', где К. обозначает положение ячейки /, а г' ограничен объемом элементарной ячейки. Этот приводит к следующей сумме по /:
|
(rK.(r)=iЈ |
|
I |
|
Ф i(k+?-K) R, |
|
Cell |
|
- i(k+<7-K) г' * V U КГ, |
|
“«(rXk(r')dr' = |
|
(8.9) |
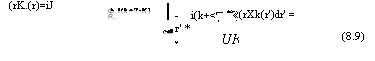 |
![]()
![]()
Где символ /се11 подчеркивает, что интеграл берется по элементарной ячейке, а Дк есть дельта-функция Кронеккера. В этом выражении мы предположили, что к и К лежат внутри зоны Бриллюэна. Если бы они были вблизи края зоны Бриллюэна, то мы учли бы процесс, при котором к + ч - К = 6, где 6 есть вектор обратной решетки. Учет этих эффектов вряд ли привнес бы что-то новое в наше рассмотрение.
Вновь используем тот факт, что только очень малые векторы ц дают вклад в потенциал, при этом разлагая огибающий интеграл для периодических частей бло - ховских волновых функций по ч:
|
|
Ортогональность волновых функций иж и ипк при том же самом волновом векторе К имеет место из-за ортогональности блоховских функций различных состояний. (Заметьте! Для различных волновых векторов периодические части не являются ортогональными). Простейшая аппроксимация состоит в сохранении только первого члена, что позволяет выделить каждую из различных зон в уравнении (8.6). С учетом (8.9) и (8.10) уравнение Шредингера в обратном пространстве принимает вид:
|
|
(8.11)
Введем огибающую функцию:
|
К |
(8.12)
Определение огибающей функции
В реальном пространстве мы можем записать (8.11) в виде:
|
|
|
TOC o "1-5" h z Х |
1К г ж 1 Ж г — ж ч 1К г
£NкaNкQ + аык+ё^ = £^^ате (8.13)
К Кц К
Или вновь в другом виде:
|
(8.14) |
![]() ^ елца*ке 'К Г + X 14 Г ^ а™'е 1К Г = ,К Г
^ елца*ке 'К Г + X 14 Г ^ а™'е 1К Г = ,К Г
43-^«мсе1Кг+К(г)^(г) = £:^(г)
/
Поскольку связанными через (8.11) являются только компоненты, близкие к К, мы можем представить дисперсионное соотношение для зоны еж в виде ряда по К Для более важного случая с К = 0 мы вводим эффективную массу т * зоны №
Ь2*2 /ок.
— о + 0 * (8.15)
2ты
При этом для упрощения рассмотрения будем предполагать ее изотропной.
|
ГК: |
![]() Подставляя (8.15) в (8.14), мы находим:
Подставляя (8.15) в (8.14), мы находим:
D3K
* ^(r)-Vv:^(r) (8.16)
Это позволяет нам получить нафаду за наши усилия, а именно — уравнение Шредингера для огибающей функции:
С„(г) = (Е~е„0К„(г) (8.17)
Уравнение Шредингера для огибающей функции
Это уравнение представляет собой основной результат настоящей главы. Оно показывает, что роль эффективной массы намного шире той, которую она играла в контексте рассмотрения, проведенного в главах 5 и 6: в случае потенциала V(r), слабо изменяющегося по отношению к кристаллическому потенциалу, волновая функция электрона в зоне проводимости N является, таким образом, волновой функцией частицы, обладающей эффективной массой, связанной с зоной N и подверженной воздействию потенциала К(г). Все влияние материала учитывается в уравнении Шредингера (8.17) эффективной массой /я* и энергией ет зоны N при К = 0.
В случае этой принятой аппроксимации полная волновая функция имеет вид:
WN= £/г)изд(г) (8.18)
При этом решение, соответствующее потенциалу V— 0 есть:
^ = ^гит(г) (8.19)
Оно отличается от точного решения заменой в (8.3) им(г) на ит (г).
В случае гетероперехода, для которого внешний потенциал V(г) претерпевает разрыв на протяжении области атомарного масштаба, вывод, который нам предстоит сделать, уже не будет строго справедливым. Если, однако, мы будем искать
Состояния, близкие по энергии к зоне проводимости, то мы сможем аппроксими
Ровать решения по обе стороны гетероперехода соотношениями (8.17) и (8.18) и использовать блоховские функции ит(г), характерные для каждого материала. Для получения стационарного состояния электрона в гетероструктуре, мы должны будем «сшить» оба решения на границе раздела (смотрите раздел 1.3.1). Начнем с того, что волновые функции должны быть непрерывными:
|
(8.20) |
Где знаки «±» относятся к материалам слева и справа от границы раздела при z= 0. В этом уравнении огибающая функция изменяется очень слабо в пределах ячейки перед границей раздела, при этом если мы используем среднюю величину (8.20) по этой ячейке, то получим:
Й/0-) = & 0+) (8.21)
Точное решение должно обеспечивать сохранение потока вероятности через границу раздела. Как было показано в разделе 1.3, поток вероятности дается соотношением:
- к: (г)у (г) - сн (о? а <г>] (8.22>
Сохранение потока вероятности при пересечении границы раздела приводит к уравнению непрерывности:
(8'23)
|
-уТ^7ТУ + К( г) 2 т„(г) |
![]() Это последнее условие может быть легко включено в рассматриваемый формализм при использовании записи уравнения Шредингера для огибающей функции в виде:
Это последнее условие может быть легко включено в рассматриваемый формализм при использовании записи уравнения Шредингера для огибающей функции в виде:
С„(г) = (Е-е„0К„(г) (8.24)
Где т (г)учитывает изменение эффективной массы при переходе от одного материала к другому.
Мы должны отметить, что этот достаточно эвристический подход скрывает ряд важных проблем. Мы ограничили нашу аппроксимацию простой зоной, где эффективная масса не зависит от К, т. е. параболической зоной (смотрите (8.15)). В том случае, когда фигурирующие энергии Е и А К(г) значительны, это предположение не является допустимым. Мы предположили также, что зона ТУ является невырожденной при К = 0, что явно не имеет места для валентных зон. Эти два аспекта (параболичность и вырождение) связаны друг с другом. Вывод огибающих функций в рамках многозонной трактовки будет основной (и проблемной) темой дополнения 8.Г. На время мы просто продекларируем, что аппроксимация огибающей функции в (8.18) вместе с соответствующим уравнением Шредингера (8.24) достаточны для квантового описания электрона в гетероструктуре.