Оптоэлектроника

Электродинамические лазерные уравнения: электромагнитные основы синхронизации мод

Вплоть до настоящего момента нас, в основном, интересовала плотность фотонов, содержащихся в лазерном резонаторе, при этом мы мало внимания уделяли волно­вой (электромагнитной) природе лазерного излучения. Напомним, что фотон есть результат квантования электромагнитной моды в резонаторе. Однако, это не осво­бождает нас от необходимости наложения на фотоны соответствующего набора граничных условий, связанных непосредственно с самим резонатором. Таким об­разом, точное описание лазерного резонатора требует решения уравнений Макс­велла, модифицированных таким образом, чтобы включить в них лазерный эф­фект. В этом разделе мы представим элементы теории мод Слэтера, что позволит нам понять расчетный метод и его приложение к синхронизации мод. Рассмотрим резонатор произвольной формы и на время будем считать его полностью пустым. Слэтеру удалось показать, что уравнения Максвелла для такого полого резонатора допускают набор решений, которые образуют полный и ортонормированный ба­зис. Более того, эти решения {Ео, Но} не зависят от времени и должны подчиняться любым другим граничным условиям, накладываемым резонатором (например, в случае граничных условий для металлических стенок, Еа должно быть перпендику­лярно их поверхности, тогда как На имеет только параллельную компоненту). Бе­зусловно, понятие ортонормированности следует понимать в терминах распределе­

Ний, т. е. /^о(г)ЕДг)сРг = 8аЪ символы Кронеккера. Более того, элементы, образую­щие двойной базис Слэтера, должны удовлетворять следующим соотношениям:

£оЕ(г) = V X Н (г) *Н,(г) = УхЕ(г)

(Напомним, что Н — вектор напряженности магнитного поля, связанный с маг­нитной индукцией соотношением Н = В///0. Заметим, что при таком определении векторы Еа и Но автоматически удовлетворяют уравнениям Максвелла в вакууме, т. е. Еа = 0 и сИуНо = 0. В дополнение к этому напряженность электрического поля Еа(т) должна удовлетворять граничному условию на поверхности:

П х Е = 0

А

Где п — вектор нормали к поверхности. Легко показать, что условие (4.В.2) и определение Но в соответствии с (4.В.1), в свою очередь, требуют удовлетворе­ния граничного условия:

П Н = 0

Вспоминая, что УхУхА=У(У*А) — У2А и используя (4.В.1), находим:

У2Ео(г) + ^Е(г) = 0 У2Н(г) + ^Н(г) = 0

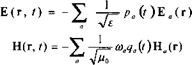Таким образом, любая электромагнитная волна при анализе в рамках максвел­ловских уравнений в любом резонаторе произвольной формы может быть разложе­на по базису Слэтера, что автоматически приводит к удовлетворению граничных условий. Таким образом базис Слэтера является более общим инструментарием для описания фотонов в резонаторах сложной геометрии, для которых плоские волны могут уже не являться правильными решениями для резонатора (и таким образом не дают возможность построить базис собственных функций). Следуя Слэтеру раз­ложение по базису можно записать в виде:

(4.В.5)

Где соа = к с/. Последние два из уравнений Максвелла действуют на разложение, приведенное в (4.В.5), и их результат может быть суммирован в виде:

Ра = Ч а

Ра = - ОіаЯа

Что является очень компактной записью с учетом экономии обозначений! Исклю­чая из этих двух уравнений, мы находим:

Ра +®аРа = 0

Последняя запись говорит нам о том, что временная зависимость конструируется из функций, осциллирующих с частотами, которые удовлетворяют требованию: о)а = к с'. К тому же, (4.В.5) напоминает нам о том, что ра и являются сопряжен­ными переменными и их квантование приведет к появлению наблюдаемых, кото­рые не будут коммутировать. Базис Слэтера приводит к очень компактной фор­мулировке уравнений Максвелла для пустого резонатора произвольной формы. В то же время остается еще проделать значительную работу по нахождению базиса {Еа, Нд}. Но несмотря на этот недостаток, предлагаемый подход значительно упрощает трак­товку проблем, связанных с колебаниями в резонаторах.

Теперь обратим наше внимание на электромагнитные поля в резонаторе, за­полненном лазерной средой с восприимчивостью х ~ Хк + Электромагнитные волны в этом лазерном резонаторе являются решениями уравнений Максвелла:

VxE(r, /) = - J-B(r,/) dt

—V х В(г, /) = i(r, /) + -^-D(r, t)

. —------------- V - , . / -у.,., .

А> Э/

Где плотность тока свободных носителей заряда Кг, С) дается законом Ома:

1(г, 0 = сгЕ(г, ?)

Обратите внимание: здесь а— электропроводность, а не поперечное сечение! Ток сме­щения Б(г, /) дается выражением:

D(r, 0 = |-[ЈE(M) + Plaser(r, t) at

В последнем уравнении Plaser есть вектор поляризации, связанный с резонансной восприимчивостью лазерной среды, тогда как поляризация основной матрицы (на­пример, кристалл YAG в лазере на основе Nd:YAG) включена в проницаемость е.

Подставляя (4.В.76) и (4.В.7в) в (4.В.7я) и проецируя уравнение (4.В.7я) на базис Слэ - тера, мы сразу находим:

(4.B.8)

Таким образом, любая мода Слэтера не связана с другими. Затем мы продифференцируем (4.В.8) и используем соотношение сопряжения (4.В.6), что приводит нас к уравнению:

(»aPa+^Pa + Pa Ј

Если а = 0 и Р1юег = 0, мы вновь получаем дисперсионное соотношение соа = кас? с новой групповой скоростью, определяемой с' = с/пор. При этом член в йра/& явля­ется членом демпфирования. Фотоны покидают резонатор с постоянной времени, которая является ни чем иным, как временем жизни фотонов в резонаторе:

(4.B.10)

Где, по определению, 0 есть добротность резонатора. В дополнение к омическим потерям (4.В.76) мы можем включить в и также и другие эффекты, механизмы диссипации, такие как пропускание зеркал. В этом случае необходимо, чтобы потери в оконеч­ных областях были усреднены по всему объему среды.

Предположим, что фотонное время жизни велико по сравнению с модовой частотой соа или вновь допустим, что добротность резонатора 0 очень велика. Ре­шениями (4. В.9) без членов источника, очевидно, являются синусоидальные функ­ции с частотами соа, которые медленно демпфируются членами типа е_1/г. Таким образом, соблазнительно выразить решения (4.В.9) в виде:

PДt)= Ра°Ч(УШ

Где (оа~ соиpa*™(i) являются слабо изменяющимися функциями (т. е., что dp/°w(/)/d/<< соJpflstow(^). В этом случае мы подставляем (4.В. 11) в (4.В.9) с тем, чтобы получить дифференциальное уравнение относительно

Уравнение (4.В.12) является наиболее общим уравнением для расчета реально­го лазерного резонатора произвольной формы и с произвольным распределением.

Для облегчения нашей физической интерпретации этого результата временно предположим, что в резонаторе существует единственная мода 1.В (4.В. 12) поляри­зация поля в лазере дается выражением:

KJr, t) = Vlase E(r, t) (4.В. 13a)

Далее, учет (4.B.5) и (4.В.11) приводит к:

Р|язе,(г,0 = —+ ix, jpr е'-'ЕДг) (4.В.136)

Ые

Где 2!^ ~ восприимчивость лазерной среды, введенная в разделе 3.3. Подставляя (4.136) в (4.В.12) и предполагая, что лазер находится в стационарном состоянии, находим самосогласованное решение относительно j и (о:

(со2-со2)+ = + UTiJ (4.В.14)

Условие (4. В. 14) является ничем другим, как условием лазерной генерации, при этом действительная часть устанавливает условие для фазы, а мнимая часть опреде­ляет условие для усиления. Например, последнее условие может быть записано в виде сг= Напомним, что (3.36) связывает мнимую часть оптической воспри­

Имчивости с усилением в виде:

(4. В. 15а)

Где п — коэффициент преломления, а к —волновое число. Условие для мнимой части (4.В.14) в этом случае может быть записано в виде:

7 = — (4.В.15 б)

СТс

Что является ничем другим, как условием генерации (4.21 б). Мы можем подобным же образом определить условие и для действительной части (4.В.14). Мы находим, что резонансная частота резонатора не является его собственным значением, но скорее она слегка смещена дефазировкой, возникающей из-за дисперсии лазерной среды. Это явление называется подтягиванием частоты.

Теперь мы используем базис Слэтера для более детального исследования меха­низма синхронизации мод в лазерном резонаторе. Предположим, что в резонаторе имеется устройство, позволяющее модулировать резонаторные потери (например акустооптическая ячейка, ячейка Поккельса и т. п., ...), как это показано на рис. 4.17. Механизм описывается модулированными потерями сг(г, t), определяемыми:

А (г, t) = <rmlcos(«m| t)fiг) (4.В. 16)

Функция /(г) является произвольной, она может быть функцией вида/(г)= S(z ~ ^), которая могла бы представлять затвор, помещенный в плоскости z = Zq - Для упроще­ния анализа исследуем отклик резонатора без учета лазерного усиления, т. е. без чле­на источника Plaser. Включение этого эффекта усложнило бы необходимые обозначе­ния без особой надобности и немного дало бы взамен в том, что касается дополни­тельной информации по интересующей нас проблеме. Сконцентрируем наше внимание на механизме синхронизации мод, который не связан с лазерной генерацией. Само собой разумеется, что в дальнейшем член Plascr надо будет вновь ввести для полного описания синхронизации мод.

Уравнения, описывающие резонатор, в этом случае даются уравнениями Максвелла:

VхЕ(г, /) = - Ав(г,/)

— VxB(r, /) = а(т, /)Е(г, /) + £ —Е(г, t)

Мо Э/

Вновь используя тот факт, что УхУхА=У(УА) — У2А и предполагая, что Е

До/Эг << Эсг£/Э/ (что вполне разумно с практической точки зрения), приходим к

Записи (4.17):

У2Е-//о<т(г,/)|-Е-//0£|^Е = 0 (4.В.18)

Дt вt

Используем теперь базис Слэтера, учитывая в (4. В. 11) выражение для /?о(/), т. е.:

Е(Г> '> = £ Т-А*" (4ВЛ9)

А Л/^О

Выражение (4. В. 18) в базисе Слэтера дает:

Slow 2 2 slow slow slow I iaj

Pa (V E„ + //0ЈE„) - (//0cr + 2moii0e)pa Ea - щcoaoa E„ - /i0fp„ e =0

(4.B.20a)

Использование (4.B.3), предположение большой величины добротности Q для резо­натора (сг/£ « со) и слабого изменения /?slow (d/slow/d/« coap^ow) позволяют нам пренебречь

Членом pilow. В этом случае уравнение (4.В.20я) приобретает вид:

To(r, О,

2е

Затем мы можем использовать выражение (4. В. 16) для модуляции потерь и спроеци­ровать полученное уравнение на моду Слэтера Е (г), что дает:

A slow _ 1 с ^ ml COS ®т1 ^ slow Л i(со,, -(oQ } _ 1 с О т[ _ slow Л i((ou-(oa±coml)t /Л D ^ t ч

Pq °q 2S P° “ aq~^Pa ’

Где Sa — интеграл перекрытия:

^ f /(r)E,(r)E,(r)d3r (4.B.22)

Wя i

Хотя внешне это и не совсем очевидно, но уравнение (4.В.21) фактически явля­ется тем уравнением, которое мы ищем. Оно показывает, каким образом возмуще­ние сгт1 связывает изначально независимые моды одну с другой. Поскольку интегри­рование (4.В.21) приводит к членам вида 1 /(соа ± сот1), ощутимые вклады будут возни­кать только при coq « соа ± сотГ Таким образом, единственными модами, предназначенными для «выживания» (по аналогии с механизмом «выживания наи­более пригодного», упомянутого ранее) будут те моды, для которых частотный ин­тервал близок к частоте модуляции comV т. е.:

$= 0)q-0)^ ,± ©_,-<> (4.В.23)

Как и в резонаторе, частотный интервал между двумя прилегающими модами является просто величиной, обратной времени обращения в резонаторе (4.25), при этом уравнение (4.23) дает условие синхронизации мод, определенное ранее в раз­деле 4.7.3. С учетом (4.В.23) выражение (4.В.21) принимает вид:

P*low = к*7 еi<5' + к*7 е - i<5/ (4. В.24я)

Где константа связи ас дается выражением:

К = _ ^.|/(r)E?(r)E, tl(r)d3r (4.В.246)

Для решения этой системы уравнений (4.В.24) запишем коэффициенты р *low в виде:

Pgslow (/) = cqQ{qSt (4.В.25)

В этом случае подстановка в (4.В.24) дает:

К к

-^ = г,+| + Г,_,

Это рекуррентное соотношение допускает в качестве решения:

(4.В.27)

Где / — модифицированная функция Бесселя порядка И наконец, электромагнитное поле в резонаторе дается (4.В. 19), что приводит к:

Где в качестве центральной частоты генерации лазерной среды мы ввели со0 (что отчасти является достаточно произвольным в контексте приведенного вывода). Уравнение (4. В.28) показывает, каким образом фазы, частоты и амплитуды различных мод жестко переплете­ны модуляционными потерями.

Таким образом, формализм мод Слэтера позволил нам показать, что модуляция по­терь в резонаторе будет приводить к синхронизации мод с частотным интервалом, при­ближающимся к частоте модуляции. Уравнение (4.В.24) показывает также, что если потери распределены однородно по всему резонатору (/(г) = const), то синхрониза­ция мод становится неэффективной. Этот механизм приложим к многим ситуаци­ям и остается безошибочным подходом для решения любой проблемы, связанной с лазерами. Наиболее общепринятый базис Слэтера, использованный до сих пор, основан на функциях Гаусса.

И наконец, следует отметить, что этот формализм описывает только среду, под­верженную неоднородному уширению, где каждая мода может осциллировать неза­висимо от других мод. В среде с однородным уширением синхронизация мод все еще возможна. В этом случае, боковые моды со0 ± qcoml создаются за счет нелиней­ного взаимодействия между лазерной средой и колебаниями модулятора сотУ В этом случае формализм, необходимый для описания возникающей синхронизации мод в резонаторе, становится существенно отличным от развитого в этом разделе.