Электрическая инжекция И неравновесная концентрация носителей
Обычно излучение света в полупроводнике происходит вследствие электронно-дырочной рекомбинации в областях, где они обладают концентрацией, избыточной по сравнению с уровнями, допускаемыми и термодинамическим равновесием. Единственным исключением в рассматриваемом случае является униполярный квантовокаскадный лазер, который мы рассмотрим в дополнении 13.И.
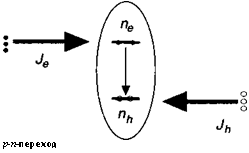
Естественно, электронно-дырочная рекомбинация имеет место в прямо смещенном р-п-переходе, где, как мы увидим, неосновные носители заряда могут сосуществовать с основными носителями на расстояниях порядка Ь0 (т. е. диффузионной длины). Этот эффект известен как электрическая инжекция (глава 10). Мы рассмотрим такой переход, в котором сходятся электронный (^4) и дырочный (JJq) потоки (здесь / и /л обозначают плотности тока электронов и дырок, а <7 есть величина заряда электрона). С учетом требования по электронейтральности мы имеем / = /л = / (смотрите рис. 13.1).
Рис. 13.1. Оптическое излучение в полупроводнике имеет место в результате рекомбинации электронно-дырочных пар в областях, где сосуществуют оба типа носителей (как это имеет место в р-п-переходе).
|
Р-п-переход |
 Сейчас проблема заключается в том, чтобы определить объемную плотность неравновесных носителей пе и пк в переходе. Это позволит нам рассчитать положение квазиуровней Ферми (7.67), скорости стимулированной (7.41) и спонтанной (7.47) эмиссии в структуре. Для этого достаточно записать для стационарных условий, что полная скорость рекомбинации Яш (см-3 с-1) в объеме V точно соответствует падающему потоку носителей, проходящих через поверхность 5, т. е. УЯ1о1 = &//<7 = ^н/Я = Исключительно с целью упрощения необходимых обозначений мы предположим, что уровень легирования вблизи перехода пренебрежимо мал по сравнению с неравновесной концентрацией носителей. Это обеспечивает выполнение пе = пь = п.
Сейчас проблема заключается в том, чтобы определить объемную плотность неравновесных носителей пе и пк в переходе. Это позволит нам рассчитать положение квазиуровней Ферми (7.67), скорости стимулированной (7.41) и спонтанной (7.47) эмиссии в структуре. Для этого достаточно записать для стационарных условий, что полная скорость рекомбинации Яш (см-3 с-1) в объеме V точно соответствует падающему потоку носителей, проходящих через поверхность 5, т. е. УЯ1о1 = &//<7 = ^н/Я = Исключительно с целью упрощения необходимых обозначений мы предположим, что уровень легирования вблизи перехода пренебрежимо мал по сравнению с неравновесной концентрацией носителей. Это обеспечивает выполнение пе = пь = п.
Полная скорость рекомбинации Яш, компенсирующей поток, входящий в область перехода, отражает вклады, по крайней мере, четырех различных механизмов, рассмотренных в предыдущих главах, а именно:
• безызлучательной рекомбинации со скоростью Лтп из-за присутствия глубоких уровней дефектов, поверхностных дефектов,... (смотрите раздел 6.5 и дополнение 5.Г);
• спонтанной излучательной рекомбинации со скоростью Вп2, где В есть коэффициент бимолекулярной рекомбинации, определяемый (7.61) и (7.62);
• Оже-рекомбинации со скоростью САи&п3, исследованной в дополнении 6. Г;
• стимулированного излучения со скоростью Я5^рЪ, где Я51 (= ЯаЬз) есть коэффициент стимулированного излучения (7.41), а есть плотность фотонов.
Для начала сконцентрируем свое внимание на поведении прибора намного ниже порога, т. е. будем пренебрегать стимулированным излучением (А^рЬ = 0). В этом случае концентрация носителей определяется стационарным условием:
Ь = %--^--А"'п+Вп1+с^ (13л)
Здесь (1 = У/Б есть эффективная толщина перехода, т. е. расстояние, в пределах которого имеет место рекомбинация. Очевидно, что в (13.1) рекомбинационные члены не эквивалентны. Первый и последний члены не генерируют свет (т. е. они являются безызлучательными) тогда, как второй член описывает спонтанную эмиссию в структуре. В связи с этим перегруппируем эти члены следующим образом:
7" = К + САи6и2
Пт
— = Вп (13.2)
^гас!
— - 1 | 1 ^пг ^гас1
Здесь: /пг и соответственно излучательное, безызлдучателъное и полное времена
Жизни. В этом случае неравновесная концентрация носителей определяется соотношением:
|
|
|
|
Эта очень простая формула является одним из основных результатов настоящей главы. Заметим:
• Полное рекомбинационное время /1о1 зависит от концентрации носителей и, таким образом, от условий функционирования. Зачастую этот параметр определяется остаточным уровнем легирования (в этом случаем мы будем заменять концентрацию носителей п в (13.3) на уровень легирования ^). В большинстве случаев этот параметр будет константой, определяемой экспериментом.
• Член Оже-рекомбинации САи&п2 зависит от концентрации носителей и его значение все более возрастает по мере увеличения концентрации.
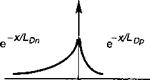
• При заданной плотности тока неравновесная концентрация носителей резко возрастает по мере уменьшения толщины активной области. В случае гомоперехода эта толщина с1 определяется Ь0п + Ь0р, где диффузионные длины неосновных носителей Ь0п (электронов в /^-области) и Ь0р (дырок в л-области) определяются (10.41) и, как правило, равны величине, лежащей в диапазоне от 1 до 10 мкм (смотрите рис. 13.2).
Определив неравновесную концентрацию носителей в (13.3), с использованием (7.67), мы можем рассчитать положение квазиуровней Ферми для каждого из типов носителей.
При выполнении этого возникают три возможные случая:
• спонтанная эмиссия доминирует над стимулированной эмиссией, и диод функционирует в электролюминесцентном или СИД-режиме;
• среда инвертирована (смотрите критерий Бернара—Дюррафура в (7.266) и (7.69)), но при этом резонаторные потери превышают усиление среды, при этом диод функционирует в режиме оптического усиления (этот режим соответствует супер- люминесцентному диоду);
• стимулированная эмиссия доминирует над спонтанным излучением, а резонаторные потери точно компенсируются усилением среды, приводя функционирование прибора в режим лазерной генерации (это соответствует лазерному диоду).
|
П, Р |
![]() В течение некоторого времени нас будет интересовать первый из упомянутых выше случаев.
В течение некоторого времени нас будет интересовать первый из упомянутых выше случаев.
|
|
|
|
Рис. 13.2. При заданном потоке носителей концентрация эленктронно-дырочных пар намного больше в гетеропереходе (б), чем в гомопереходе (а), где более эффективна диффузия носителей.
Пример-----------------------------------------------------------------------
Пусть при определенных условиях гетероструктура А10 25Са0 75А8/СаА8 толщиной й = 10 нм обладает полным рекомбинационным временем жизни величиной 5 не. Ток величиной 1 мА, пересекающий сечение перехода 10 мкм х 100 мкм приводит к неравновесной концентрации носителей (13.3):
П = 10'3Лх5х 10~9 с/(ю-5 см2 х1,6x10-’ КлхКГ6 см)=3,1х1018 см'3
Поскольку эта концентрация носителей превышает эффективную плотность состояний в зоне проводимости УУ = 4,3 х 1017 см-3, электронный газ будет вырожденным, и в этом случае положение квазиуровня Ферми для электронов (5.566) составит:
ЕГп - Ес= (1,05х 10"34 Дж)2/(2х0,067x0,9Х10-30 кг) (зЛ 3,1x1024 м 3)2/3/1,6х 1(Г19 Кл = 116мэВ
Соответственно концентрация дырок р (= п) меньше эффективной плотности состояний в валентной зоне = 1,3 х 1019 см-3, при этом положение квазуровня Ферми, определяемое (5.47), составит:
ЕГр - Еу = 0,0259 эВх1п(1,Зх109/Зх1018)= 38 мэВ
В рассматриваемом случае энергетический зазор между электронным и дырочным квазиуровнями превышает ширину запрещенной зоны, т. е.:
(£>„ - Ес)~ (Ег„ - Еу)= 116 - 38 мэВ > 0
При этом в соответствии с критерием Бернара—Дюррафура система инвертирована.