Эквивалентность А Р — и йА-гамильтонианов и правило Томаса—Райха—Куна
Определенный ряд общих заключений по поводу различных величин, влияющих на оптические свойства (силы осцилляторов, ...), может быть извлечен из коммутационных свойств наблюдаемых р и г. В этом разделе мы будем обращаться только к операторам, и это позволит отбросить символ «А», который в других случаях позволял отличать операторы от наблюдаемых. Начнем мы с того, что покажем эквивалентность Ар - и Б р-гамильтонианов.
Мы напоминаем, что два типа гамильтонианов могут использоваться для описания взаимодействия между квантовой системой (описываемого гамильтонианом Н0 = р2/2т + К(г)) и электромагнитной волной (смотрите (3.12) и (3.13)):
Гамильтониан Ар: — А±(г0, г)р
Т (З. Г.1)
Гамильтониан Б Е: ^>£(0 = “<7Е(г0, /)
Для плоских волн векторный потенциал и электрическое поле даются соотношениями (3.5а) и (3.6):
Е(г0, /) = Е0со8(к г0 — Ш)
Е (З. Г.2)
Л±(го,0 = — вт(к г0 - ш)
О)
Напомним, что г0 обозначает положение квантовой системы, и оно может быть принято за начало отсчета. Для того, чтобы упростить обозначения, мы можем предположить, что А± и Е ориентированы вдоль оси 01- В этом случае уравнения (З. Г.1) могут быть записаны в виде:
¥Арсо& оА = -— — ргсо%оА
Т т (З. Г.З)
IV Ое (0 = №ое ш - - дЕ01 бш Ш
Мы видели, что скорости переходов, которые входят в выражения для поглощения, используют элементы типа (fzi) или (/|р |/‘) Таким образом мы будем искать связь между этими двумя членами. Для этого используем коммутатор I и #0:
|
2т |
|
■ 2~ (ЗР, ^РІ ~Р&1 + Рг^г - Рг) = |
|
Т |
|
|
|
|
|
Будучи спроектированным на состояния |/) и |/) уравнение (З. Г.4) приобретает вид:
= </|Ь, Я0]/) = {е, - Егущ <3‘Г5>
Из этого соотношения может быть установлена связь между двумя матричными элементами:
Связь между матричными элементами гл рг
Подстановка (З. Г.6) в (З. Г.З) дает:
(З. Г.7)
./ г ' /і#г і * /
Т со со
Это соотношение устанавливает эквивалентность двух гамильтонианов только в условиях резонанса. Сила осциллятора в рамках А р — подхода записывается в виде:
|
(З. Г.8) |
![]() 2
2
|
Л. = |
![]() ■К'М2>г
■К'М2>г
Сила осциллятора для перехода 1 -> 2 с использованием А р-гамильтониана
Предпочтительное использование матричных элементов гамильтониана БЕ (3.40) или Ар (З. Г.8) прежде всего зависит от контекста самого использования. В общем случае мы можем сказать, что Ар-гамильтониан лучше подходит для рассмотрения переходов, связанных с делокализованными состояниями (т. е. состояниями импульса), что встречается при описании межзонного поглощения в полупроводниках. В то же время БЕ-гамильтониан больше подходит для описания переходов между локализованными состояниями (глубокие дефектные состояния, квантовые ямы и т. д.)
Теперь продемонстрируем еще другое следствие этих правил коммутации. Рассчитаем сумму сил осцилляторов для переходов между |/) и всеми возможными конечными состояниями |/):
|
2т |
![]()
|
Л = |
![]() (З. Г.9)
(З. Г.9)
/*» /*'
Это последнее уравнение может быть существенно упрощено. С одной стороны:
|
Ф) |
![]() X £/№>12=X £/(Ф1/)(/1Ф)=(Ф '£е//){/
X £/№>12=X £/(Ф1/)(/1Ф)=(Ф '£е//){/
Предположим, что базис собственных векторов |/) является полным. Это означает, что любое состояние системы |п) может быть разложено однозначно в этом базисе:
(З. Г.10)
(З. Г.11)
Выражение для гамильтониана через собственные энергии и состояния
Это последнее уравнение может быть объяснено с учетом того, что, если (З. Г.11) выполняется для всех собственных состояний |/), оно также должно выполняться для любого произвольного состояния |п). В этом случае мы имеем:
|
|
|
(З. Г. 12) |
![]() /
/
|
Легко может быть доказано следующее соотношение свертки: |
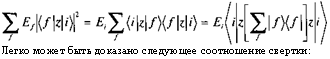 Второй член правой стороны (З. Г.9) может быть записан в виде:
Второй член правой стороны (З. Г.9) может быть записан в виде:
(З. Г. 13)
|
/ |
(З. Г. 14)
Соотношение свертки для полного базиса собственных векторов и наблюдаемых
Где 1 есть оператор тождества. Таким образом мы имеем:
|
/ |
(З. Г. 15)
При использовании (З. Г. 12) и (З. Г. 15) уравнение (З. Г.9) приобретает вид:
|
|
(З. Г. 16)
Теперь, исходя из (З. Г.4) можно записать:
|
|
(З. Г. 17)
А также:
(«к, Я„] г] /) = (і|М„г - Я0г2 - г2 Я„) /) = 2(/ zH. z - Я0г21 /) (З. Г. 18)
Поскольку (/|#0£2|/) и </|г2#0|/> оба равны £.(/|г2|/). Подставляя (З. Г. 17) и (З. Г. 18) в (З. Г. 16), мы получаем:
|
|
(З. Г. 19)
Правило суммы Томаса—Райха—Куна
В сочетании с формулой для поглощения в многоуровневой системе (3.41) дает:
|
|
(З. Г.20)
Правило суммы (З. Г. 19) может быть интерпретировано следующим образом: классическое выражение для поглощения а — Ы]д2л:/(2€0тсп)1(у), которое может быть получено в контексте модели упруго связанного электрона, остается действенным в квантовой механике. Единственно, это поглощение распределено между различными осцилляторами, а также переходам между разлными осцилляторами, соответствующими переходам между различными квантовыми уровнями системы. При этом в указанное распределение в качестве весовых множителей входят силы осциллятора, калибрующие интенсивность каждого их переходов. Несмотря на это, сумма этих сил осциллятора равна единице. Выражаясь более эмпирическими терминами, если мы рассмотрим полную кривую поглощения для квантовой системы, отношение интегрального поглощения к заселенности основного уровня составляет:
Я2я
|
N. |
![]() 2єптсп
2єптсп
Оно то же самое для всех систем. Эта концепция раскрывает свою полную силу при осознании того, что сила осциллятора может быть отрицательной (смотрите сноску к (3.41)). Мы возвратимся к этому аспекту позже при рассмотрении межподзонных переходов в квантовых ямах.
Пример: силы осциллятора в бесконечной квантовой яме--------------------------------------
Проиллюстрируем концепцию силы осциллятора на примере достаточно простого случая бесконечной прямоугольной ямы. Мы видели в разделе 1.4.2, что собственные энергии и собственные функции стационарных состояний для квадратной потенциальной ямы шириной а с бесконечно высокими потенциальными барьерами в
О и ©о даются соотношениями:
П2л2
|
2т а2 |
![]() Еп = п
Еп = п
I
|
(З. Г.22) 6х»(/-у>-1] (З. Г.23) |
![Эквивалентность А Р - и йА-гамильтонианов и правило Томаса—Райха—Куна подпись: (з.г.22)
6х»(/-у>-1] (з.г.23)](/img/683/image535.gif) П) = A^^-sinn—z 1 1 а а
П) = A^^-sinn—z 1 1 а а
В этом случае матричные элементы (/1 г[/) даются интегралами:
('к|у) = — zsini—г мп у — = -^
' 1 1 ' а] а а п
И:
|
&)■ |
![]()
|
(З. Г.24) |
![]() -Ні-])
-Ні-])
Где /(/ —у) равно 0, если (/ —у) четное число и 1, если (/ —у) — нечетное число. В этом случае сила осциллятора для перехода / —»у дается соотношением:
|
(и)2 |
|
Л2ж2 |
|
2т |
|
О2-/2) |
|
Л = |
|
2та |
|
*4 О'2-'2)4 |
|
2 а2 |
|
|
Таким образом:
|
Л' - ■ |
![]()
|
(З. Г.26) |
Сила осциллятора для перехода / —> У в бесконечной квантовой яме
Мы можем проверить правило суммы, используя разложение в ряд для л2. Заметим, что сила осциллятора сконцентрирована на переходах между наиболее низкими энергетическими уровнями. Говоря более точно, сила осциллятора /, начиная с основного уровня |1) уменьшается как 1/у4, при этом первые два последовательные члена имеют вид:
71 5