Эффективная масса и плотность состояний
Обе модели (жесткой связи или почти связанных электронов) приводят к одному и тому же результату в том, что касается дисперсии энергии Е (к) вблизи экстремумов валентной зоны и зоны проводимости kext (смотрите дополнения 5.А и 5.Б). В обоих случаях мы приходим к квадратичной зависимости Е от к, представляемой матричным произведением:
£(к) = Е'Я + - у(к - Kext)' М -'(к - kext) (5.14)
Где А — транспонированный вектор Ли М — действительная симметричная матрица, называемая матрицей эффективной массы по причинам, которые будут разъяснены позже. После диагонализации матрицы М~1 мы видим, что зонная структура может быть записана в виде:
|
Е(к) = Е'»+^ |
![]() (K - kext t У ^ (к2 — ktxt 2 У ^ (къ — kext 3 У ^ ^
(K - kext t У ^ (к2 — ktxt 2 У ^ (къ — kext 3 У ^ ^
/я, т2 тъ
Где к. и kexi. являются компонентами к и kext так же, как собственные векторы М~1. Мы узнаем выражение, связывающее энергию и волновой вектор свободных электронов (Е = h 2к2/2т), но с другой массой. Это и есть эффективная масса, обусловленная взаимодействием электронов с периодическим потенциалом кристалла. Эффективная масса положительна, когда кривизна такова, что направляет дисперсионную зависимость вверх, и отрицательна, когда дисперсионная зависимость направлена вниз. Значение этой отрицательной эффективной массы мы рассмотрим позже. Поверхности постоянной энергии, получаемые при Е= const образуют эллипсоиды, центрированные вблизи экстремумов зоны Бриллюэна. Рисунок
|
|
|
Si |
|
GaAs |
|
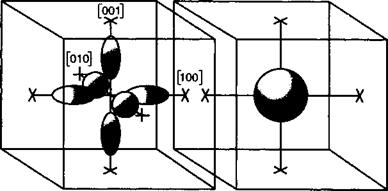
Рис. 5.8. Эллипсоиды постоянной энергии в Si и GaAs. |
5.8 иллюстрирует такие эллипсоиды постоянной энергии вблизи экстремумов зоны проводимости и валентной зоны кремния. Как следует из таблицы приложения (стр. 588) кремний характеризуется двумя эффективными массами — одной в поперечном направлении тйХ и другой — в продольном направлении теУ
Для большинства полупроводников валентные зоны вырождены при к = 0. Причиной этого является преимущественно триплетная природа sp3-орбиталей, формирующих валентную зону. Однако вырождение снимается при к ф 0, что приводит к подзонам с различной кривизной. При этом подзоны с малой кривизной обладают большей эффективной массой. Такие подзоны называются подзонами тяжелых дырок (позже мы объясним, что мы подразумеваем под понятием дырка). И напротив, подзоны с большей кривизной называются подзонами легких дырок. В таблице приложения (стр. 588) представлены различные эффективные массы в Si и Ge.
Теперь нам предстоит рассчитать плотность состояний в различных разрешенных зонах. Этот параметр имеет фундаментальное значение во всех расчетах, связанных с переходами между зонами. Для того, чтобы без необходимости не перегружать систему обозначений, временно сконцентрируем свое внимание на простом примере, связанном с зоной проводимости GaAs, где эффективная масса является изотропной. В этом случае зонная структура дается выражением:
SHAPE \* MERGEFORMAT ![]()
|
(5.16) |
![]() Е(к) = Е' + + к] + К) = Ес +
Е(к) = Е' + + к] + К) = Ес +
2
|
2 тс |
![]() Тс
Тс
Где к есть модуль волнового вектора к, а Ес — энергия минимума зоны проводимости. Мы можем легко рассчитать плотность состояний в к-пространстве. Уравнение
(5.10) показывает, что в объеме с!3к = дкйкдк1 в предположении цикличных граничных условий Борна—фон Кармана имеется (УУях)(УУя )(Иа )/8я3 =^78я3 состояний. Если бы мы использовали граничные условия в (^.9), плотность состояний составила бы У/Ък3, но объем интегрирования в этом случае (при положительной величине л2, п3) был бы в восемь раз меньше. Плотность состояний в ^-пространстве есть бесконечно малое число состояний = р(к)сРк, расположенных в
Элементарном объеме сРк:
|
|
(5.17)
Плотность состояний в /с-пространстве с учетом периодических граничных условий и в пренебрежении спином электрона
|
2т* |
|
Где т* — средняя эффективная масса зоны проводимости, которая определяется соотношением: |
|
Т* = (птУ2та) |
|
2т* |
|
1/2 |
|
(Е-Ес) |
|
1/2 |
|
~ Е) |
|
,3/2 |
|
1/2 |
|
(Е-Ес) |
|
1/2 |
|
К2йк -2 |
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
|
|
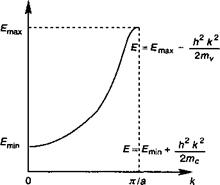
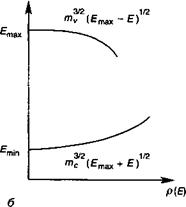 Рис. 5.9. Зонная структура (а) и плотность состояний (б) вблизи экстремумов зон разрешенных состояний.
Рис. 5.9. Зонная структура (а) и плотность состояний (б) вблизи экстремумов зон разрешенных состояний.