Оптоэлектроника

Эффект спонтанной эмиссии и фотонная конденсация

Как упоминалось ранее в главе 4, мы пренебрегли влиянием спонтанной эмиссии на лазерный эффект. Одним из следствий этого упущения, которое мы специально отметили в разделе 4.6, является то, что стимулированное излучение не может начать­ся, если первоначальное число фотонов в резонаторе равно нулю. Другими словами, число фотонов р = 0 в моде 1 при плотности инверсной заселенности п = nd= const дает допустимое решение (4.34) и (4.35). Теперь мы покажем, каким образом спон­танная эмиссия может быть включена в лазерные уравнения и обсудим влияние этих эффектов на лазерные характеристики. Для начала возвратимся к двум связан­ным уравнениям (4.34) и (4.35), описывающим динамическую связь между числом фотонов р в данной моде 1 и плотностью инверсной заселенности nd =п2 — для четырехуровневой системы в резонаторе:

(4.А.1)

Т2 Тс ^thresshold

= + (4.А.2)

Тс Тс ^threshold

Напоминаем, что Я есть скорость накачки уровня |2), т есть фотонное время жизни в резонаторе и «threshold = 1/с'гбгор — плотность инверсной заселенности, необ­ходимая для достижения лазерного порога. Предположим также, что время жизни на уровне |1) достаточно мало для того, чтобы позволить нам пренебречь плотно­стью заселенности пх (где nd ~ я2), и следовательно = т2 (уравнение (4.6)). Спон­танная эмиссия вводится в (4.А.1) включением 1// при расчете 1 /г2, как это мож­но увидеть в уравнении (4.2). С другой стороны, в (4.А.2) мы должны отразить тот факт, что даже в отсутствии каких-либо фотонов в резонаторе (р = 0) фотоны могут освобождаться через спонтанную эмиссию. В главе 3 мы видели, что скорость эмиссии в двухуровневой системе может быть записана в виде W(P + 1), где Р есть число фотонов (а не плотность фотонов), WP есть стимулированное излуче­ние и W — спонтанное излучение (уравнение (3.66)). Таким образом, для включе­ния эффектов спонтанной эмиссии достаточно выразить (4.А.1) и (4.А.2) через чис­ло, а не плотность (умножая на объем резонатора), и заменить Рна Р + 1 в (4.А.2), при этом мы получаем систему связанных уравнений:

D Nd RV Nd P Nd

^ T2 Tc ^threshold (4.A.3)

&P_ = _P_ P +1 N, dt + t, Ntl

Динамические уравнения лазера с учетом спонтанной эмиссии

В (4.А. З): = паУ и Р = р¥ Более того, эти уравнения предполагают, что

Существует единственная мода в резонаторе, в которую переходят все спонтанно излученные фотоны (т. е. коэффициент спонтанной эмиссии Д введенный в (3.72), равен 1). Теперь введем безразмерную переменную:

Г = —(4.А.4)

Threshold

И напомним, что:

D _ ^threshold. „ _ 1 Р _ ^ у _ nd (4.А.5)

Threshold “ » "threshold “ / » ''sat ~ / » л ~ v 7

^2 C ^op^c C ^op^ ^threshold

При всех изменениях переменных для стационарного состояния (4.А. З) может быть записано в виде:

R = X 1 +

Х(Р + ) = Р

Из решения результирующего квадратного уравнения тривиально находится число фотонов Р:

(4.А.7)

Число фотонов в резонаторе в функции скорости (безразмерной) накачки

Это внешне невинное уравнение в действительности подразумевает существо­вание достаточно любопытного физического эффекта, который мы теперь и иссле­дуем. Начнем с того, что отметим Р^ — очень большое число, как правило ~1010, что придает уравнению достаточно необычный характер.

При уровне накачки, слегка большем порогового (г = 1 + 8), член 4г/Рт под знаком радикала мгновенно становится пренебрежимо малым по сравнению с г/, что приводит к Р = ^(-1), а это как раз то, что описывается (4.28). В случае уровня накачки слегка выше порога (г = 1 — 8) (4.А.7) приобретает вид:

Р =

2

(4.А.8)

Или

	-8
(4.А.9)

Другими словами, если система находится в состоянии настолько ниже порога, то число фотонов хорошо аппроксимируется соотношением:

(4. А. 10)

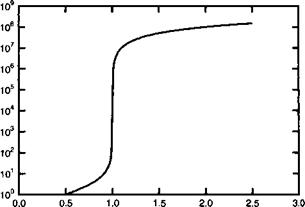
Таким образом, при переходе от накачки с уровнем на 1% ниже порога к накач­ке с порогом на 1% выше порога число фотонов в резонаторе изменяется от 102 до х 10-2 ~ 108. Это соответствует подлинной фазовой конденсации, что является следствием бозонной природы света, если принять во внимание наличие члена Р + 1 в (4.А. З). Рисунок 4.А.1 иллюстрирует поведение числа фотонов в резонаторе как функцию приведенной скорости накачки г при Р^ = 108 фотонов.

Подчеркнем теперь важное следствие спонтанной эмиссии для динамики ла­зерного резонатора, которое мы используем в дополнении 4. Г. Второе динамичес­кое уравнение в (4.А. З) может быть переписано в виде:

Где <7 — оптическое усиление при одном проходе света по длине резонатора (£« gc^), g — усиление на единицу длины (см-1), определяемое соотношением g = И/7ор, а тш — время прохода света между двумя резонаторными зеркалами. Уравнение (4.А.12) можно легко решить, что дает:

Е(с/т^,-1/тсУ _ *

Р = - г-1---------- Г~^ <4А13>

1 - КГш /тс°)

1 light

Таким образом, даже в том случае, когда в резонаторе нет фотонов в момент времени t = О, механизм лазерной эмиссии будет запускаться спонтанной эмиссией одного фотона в моду до тех пор, пока будет справедливо условие G> W7c = 2r (усиление превышает потери на зеркалах).

Более того, уравнение (4.А. 13) показывает, что фотонная заселенность форми­руется шумом с характерным временем формирования ть, которое может быть лег­ко рассчитано в предположении, что G0 » 1 /г (G0 есть первоначальное ненасы­щенное усиление), т. е. когда пропускание зеркала мало. В самом деле, в этом случае (4.А.13) может быть записано в виде:

(4.А.14)

С характеристическим временем формирования лазерного процесса ть, определяемым:

^ light L! С 1

Т> к —___

(4.А. 15)

Характеристическое время формирования лазерного процесса

Теперь вспомним, что у0 есть ненасыщенное усиление лазерной среды.

Многими авторами вводятся другие параметры (и даже в большей степени про­извольно) для того, что мы называем временем формирования лазерного процесса. Это есть время необходимое, чтобы лазер смог генерировать излучение с измеримой мощностью Рот, беря в качестве исходной точки мощность шума Р0. В соответствии с (4.А.14) это время формирования дается соотношением:

Tb = log(Pm/P0)rb = g(Pm /P0)-L (4.A.16)

Гос

Время формирования лазерного процесса

Обычно величиной, принимаемой для log (PJPQ), является 30, что соответствует пороговой мощности детектирования 1 мВт и мощности фотонного шума 10-16 Вт.

Пример---------------------------------------------------------------------------------------------------------------------------------------------------

В том случае, когда лазерное усиление мало, время формирования может быть достаточно большим по сравнению с другими характеристическими временами в резонаторе. Если мы предположим, что лазерная среда характеризуется ненасыщен­ным усилением величиной 0,01 см-1, а скорость света составляет с' = 2 х 1010 см/с, то характеристическое время формирования гь = 5 не, а время формирования tb составляет 30 ть, т. е. 150 не.