Оптоэлектроника

Динамические аспекты лазерных диодов

Динамические характеристики лазерных диодов могут быть исследованы с исполь­зованием процедуры, аналогичной подходу, использованному в разделе 4.7. Одна­ко, лазерные диоды вводят новые характеристики, которые должны быть включе­ны в связанные динамические уравнения (4.34) и (4.35). Модифицируем эти урав­нения с тем, чтобы включить в них особенности, связанные с функционированием лазерного диода:

6.п Г п

D, «d ■<*«*■-о

^7 = C'g(n М" - "і,- —

D t т

Динамические уравнения полупроводникового лазерного резонатора

Первые два члена в первом уравнении описывают поступление электронно­дырочных пар вследствие тока инжекции, а также потери пар из-за всех рекомби­национных механизмов за исключением стимулированного излучения. Третий член отражает вклад стимулированного излучения, и он равен концентрации фотонов в резонаторе (см-3), умноженной на произведение #(п)(п — л1г)(где (п — п1т) дает кор­рекцию на необходимую концентрацию прозрачности полупроводникового лазе­ра); с' = с/пк есть групповая скорость фотонов в полупроводнике, через которую можно установить соотношение между фотонным потоком и концентрацией (смот­рите главу 4). Член #(п) (см~1/см~3 или см2) описывает изменение динамического усиления в функции концентрации носителей:

*(и)=42- (13.70а)

Ап

Этот параметр является также характеристическим наклоном кривой g(n) смотрите рис. 7.8 для лазеров с гетеропереходами и рисунок 13.22 для квантово-размерных лазеров). В случае лазеров с гетеропереходами это усиление является константой, определяемой (13.21):

Здесь п = п$/с1. Сравнивая (13.69) с (4.1), мы находим, что динамическое усиление есть понятие, очень близкое к оптическому поперечному сечению аор в атомной фи­зике. Не было бы преувеличением рассматривать динамическое усиление как попе­речное оптическое сечение для каждого электрона в полупроводниковой среде, Мы увидим, что это оптическое поперечное сечение в случае полупроводников значи­тельно: несколько 10~16 см2 в сравнении с 10~19 см2 в легированных ионами (Сг, N(1, ...) лазерах. Это и объясняет очень большие усилительные характеристики полу­проводниковых лазеров.

Во втором уравнении (13.69) третий член отражает создание фотона в волновод­ной моде (и следовательно, с влиянием Г). Второй член отражает резонаторные потери (рассеяние света, потери на зеркалах и т. д.) через эффективное фотонное время жизни г, которое, как мы напоминаем, равняется (смотрите (4.24) и (13.27):

__________ 1__________

С'|«, + (1/21)1п(1/Лт1/0] (13.71)

Расчет динамических характеристик лазерного диода проводится по традици­онным правилам (смотрите раздел 4.7). Предположим, что усиление #(л) = £ не зависит от п для малых сигналов. Обозначим через п0 и 50 соответственно концент­рации электронов и плотности фотонов в стационарном состоянии. Они определя­ются стационарными решениями (13.69):

1

П{„ - п, г =

С^Г тс

(13.72)

Я<1 С 1

С использованием этих уравнений мы вновь легко приходим к результатам, полученным в (13.34) для мощности лазерного излучения в функции тока возбуж­дения. На самом деле нас интересует малосигнальная динамическая характерис­тика при токовой модуляции / = /0 + £/ (при 8Г « /0). Таким образом, мы записываем концентрации пар носителей и плотности фотонов в виде п = п0 + дп и

5 = 50 + 8б. Пренебрегая членами второго порядка, мы находим следующую систему дифференциальных уравнений в малосигнальном пределе:

(13.73)

— = ГС£50&2

Здесь мы использовали (13.72). Исследуем теперь гармонический отклик системы, принимая:

Д] = Re8j(co)eш,\ дп = Яе рп(со)еш ]; 8б = Яе |&(су)е!<у' ] (13.74)

В этом случае система дифференциальных уравнений (13.73) приводит к:

&(а>) _ ____________ (<5/ / дё )Гс'#___________

*0 - 0)2 + [0 / '.о. )+ + С'«50 / Тс

В этом случае малосигнальный отклик дается выражением:

|&И =---------------- /г=--------- - ................................................ ................. (13.76)

(*с/с'&он№ - (<Фо /ОГ + ®2[0 /0+ с'&оУ

Этот отклик максимален на частоте релаксации юЛ:

Щ = 1(_|_ + «ф0] . 1И& (13.77«)

V Ь 2^/,0, ) 1 *'

Частота релаксации полупроводникового лазера

При этом коэффициент демпфирования Гк определяется выражением:

Г« « ^ (13.776)

Физическая причина колебаний и релаксации обсуждалась ранее в разделе

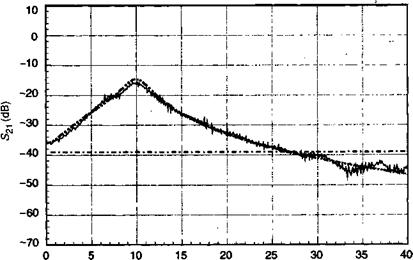
4.7.1. Эти явления соответствуют колебательному обмену энергией между элект­ронно-дырочными парами и фотонной заселенностью, охваченными взаимодей­ствием через стимулированное излучение. Говоря более точно, по мере того, как увеличивается плотность электронно-дырочных пар, также возрастает и усиле­ние, которое запускает механизм увеличения фотонной плотности, что приводит к увеличенной скорости стимулированного излучения, которое уменьшает кон­центрацию носителей (за счет рекомбинации), приводя к колебаниям этих пара­метров. Релаксация происходит из-за потери фотонов (за счет паразитного погло­щения или за счет потерь на зеркалах), что описывается г, как в (13.77б). Рисунок 11.28 демонстрирует частотную характеристику полупроводникового лазера. Ха­рактер поведения, предсказываемый выражением (13.76), воспроизводится экспе­риментально, демонстрируя начальное возрастание до максимальной величины с последующим спадом пропорционально /~2. Уравнение (13.77а) предсказывает также увеличение релаксационной частоты с возрастанием тока накачки с учетом зависимости /Л от 501/2. Наконец, мы отмечаем, что максимальная частота эксплу­атации (т. е. частота, при которой вблизи /^ЗБ(а)) = |<£у(0)|) возрастает с увеличе­нием наклона g(n) (или g(J)). Таким образом, квантово-размерные лазеры облада­ют существенным преимуществом перед объемными лазерами с учетом их лучше­го динамического усиления.

Пример----------------------------------------------------------------------------------------------------------

Найдем частоту релаксации гетеролазера на основе ОаАз/АЮаАБ. Необходимые для этого параметры есть:

Выходная мощность, Ром = 10 мВт Энергия фотонов ку= 1,4 эВ

Коэффициенты отражения выходных зеркал, Ят1 = 1, Ят2 = 0,32

Площадь области оптической моды А = м/тос1е, где и> (ширина резона­тора) = 2 мкм и ^тос|е (эффективная глубина моды) = 0,1 мкм, что дает А = 2 х 10~9 см2.

Длина резонатора Ь = 200 мкм

Паразитные потери ар = 10 см-1

Коэффициент оптического преломления пх = 3,3

Квантовая эффективность т/ = 1

Динамическое усиление g, определяемое рис. 7.8, есть 3 х 10~16 см2 Фотонная плотность 50 определяется (13.32), что мы перепишем здесь в виде:

Zf - = (1 - R)—h(os0 А и„

Это приводит к фотонной плотности 50 величиной 3,6 х 1015 см-3. Фотонное время жизни в резонаторе есть 1 /(?(а — 1/21п(/?)) или 2,8 пс. Таким образом, релак­сационная частота есть: