Оптоэлектроника

Брэгговские волноводы

Мы увидим, каким образом уравнение связанных мод (9.39) позволит нам изучить поведение волноводной волны в оптическом волноводе, гофрированном с перио­дом L (смотрите рис. 9.Б. 1). В том случае, когда длина периода гофра равна длине волны распространяющегося излучения (т. е. 2тт/Я), гофрированная часть волно­вода действует как брэгговский отражатель (смотрите дополнение 9.Г.1). Эта си­туация, относящаяся к распространению фотонов, аналогична случаю, рассмот­ренному в главе 5, относящемуся к электронам в твердых телах (приводящему к образованию разрешенных энергетических зон). Брэгговская решетка может быть представлена периодической модуляцией относительной проницаемости. Для на­чала предположим что эта модуляция изменяется синусоидально как:

(9.Б.1)

Возмущающая поляризация, вызванная этой модуляцией, дается в этом случае выражением:

Л.« = e0Ae(r)E(r, t)

Электромагнитное поле в волноводе Е(г, /) может быть разложено по базису собственных волноводных функций, как это описывается (9.34). С использованием (9.Б.1) и (9.Б.2) возмущающая поляризация может быть записана в виде:

,+е№ - к. с. = (^)e“i(A-±(2,r/A)k J£дг(х)[£'т(х)£'/(х)](Ьс

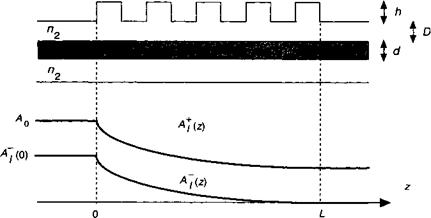
Рис. 9.Б.1. Геометрия брэгговского волновода.

Мы благоразумно сохранили две противонаправленные моды А+ и А~, т. к. мы ожидаем их связь за счет гофра в виде дифракционной решетки. Уравнение (9.Б.4) связывает различные амплитуды Ат(г) через связанные дифференциальные уравне­ния. Мы можем избежать массы ненужной работы, исследуя это уравнение. В (9.Б.4) введены два типа констант распространения:

А

Эти константы связывают дА^/дг с А~. Кроме того:

Р„,+р,±^-

А

Эти константы связывают дА~/дгс А

Первый случай нас не интересует, хотя он и обеспечивает возможность рас­смотрения задач, связанных с дифракцией Фраунгофера в ближнем поле. В то же время нас интересует второй случай, устанавливающий связь между падающей вол­ной с индексом / справа со второй волной с индексом т слева. Говоря более точно, мы имеем дело со специальным случаем I = т, т. е. случаем, соответствующим отражению. В (9. Б.4) мы сохраняем только те члены, для которых рассогласование фаз 2Д/? близко к нулю, поскольку только эти члены, в конце концов, будут интер­ферировать конструктивно. Это фазовое рассогласование дается соотношением:

АР = Р,~ (9.Б.5)

А

Фазовое рассогласование в брэгговском волноводе

Это последнее условие может интерпретироваться как условие сохранения пол­ного волнового вектора. Периодическая решетка обеспечивает волновой вектор - 2ж /Л, который вычитается из волнового вектора падающей волны /3 + и генерирует волновой вектор, соответствующий отраженной волне Р~ (смотрите рис. 9.Б.2). В этом случае уравнение (9. Б.4) может быть разделено на два связанных уравнения:

Рис. 9.Б.2. Интерпретация условия со­гласования по фазе брэгговского вол­новода с использованием концепции со­хранения волновых векторов.

Л

Е1 <-----------

±АГ (?)=-&; ЬУ1[13]

±а;{і)=+8а;{іУ^

Уравнения связанных мод брэгговского волновода

Здесь константа связи g дается выражением:

£ = — (9.Б.6 б)

8д, I

Исходя из (9.Б.6) можно легко показать, что:

7-(к|2 + кП=° (9.Б.7)

61 '

Это означает, что суммарная оптическая мощность двух мод остается постоянной.

Связанные уравнения (9.Б.6) можно решить стандартными методами, а имен­но: подставляя одно из уравнений в другое, что, например, дает:

2

-НАр 4-Л,[14]-е2А,* = 0 (9.Б.8)

<1?

Амплитуды А* и А' являются, таким образом, линейными комбинациями экс­понент аргументов:

А = Ар±6 (9.Б.9 а)

Здесь £есть дискриминант (9.Б.8):

5 = Л/Р"ЩГ (9.Б.96)

Для получения полного решения наложим граничные условия на амплитуды в волноводе. Волна падает слева с амплитудой А0 на вход дифракционной решетки (г = 0) (смотрите рис. 9.Б.1). В то же время никакая волна не падает слева на выход волновода при I = Ь. В этом случае граничные условия имеют вид А+ (0) = А0 и А~(1) = 0, при этом решения (9.Б.6) легко находятся в виде:

(9.Б.10й)

Р + 1Д&

Рисунок 9.Б.1 иллюстрирует для этого случая поведение квадрата амплитуд (т. е. оптической мощности на единицу ширины волновода) в функции расстояния. Падающая волна А* экспоненциально затухает в области решетки, порождая отра­женную волну А~. В том случае, когда произведение ЗЬ достаточно велико, т. е. если решетка достаточно эффективна, Л“(0) по порядку величины близка к Л0, тогда как А?(Ь) ~ 0. В этом случае перенос энергии является полным, и область решетки ведет себя как брэгговский отражатель.

Этот брэгговский отражатель обладает характерной для него спектральной шириной полосы, определяемой требованием, чтобы £было действительной величиной, т. е. с учетом (9.Б.9я):

71

±-,<АЙ<т - + *

А Л

(9.Б.11)

Спектральная ширина полосы брэгговского отражателя

Таким образом, ширина полосы, выраженная в волновых числах, составляет 2g. Рис. 9.Б. З дает типичный пример пропускания брэгговского волновода, опи­сываемого соотношением:

_

И/(о)|2 ”

Условие (9.Б. 11) так же, как выражение для пропускания волновода (9.Б.12я) показывает, что произведение gL управляет максимальной эффективностью брэг­говского волновода. В резонансе при А/? = 0 пропускание дается формулой:

(9.Б.12 б)

Если коэффициент связи g мал, брэгговский волновод должен иметь достаточно большую длину с тем, чтобы выполнялось неравенство » 1. Для понимания роли различных параметров (а также того, каким образом их следует комбинировать для обеспечения эффективного брэгговского волновода) мы попытаемся вывести выра­жение для эффективности волновода с сильным ограничением.

Рассмотрим волновод толщиной с! и коэффициентами преломления лЦ и у1е2 соответственно для слоев сердцевины и ограничения (смотрите рис. 9.Б.1). В пред­положении распространения Г^-волны в волноводе с сильным ограничением (9.13) дает для величины, обратной длине волны, а и глубины туннельного проникнове­ния к следующие аппроксимирующие выражения (смотрите (9.23б)):

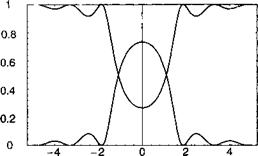
Рис. 9.Б. З. Зависимости коэффициен­тов пропускания и отражения брэггов­ского волновода от нормированного рассогласования фаз A/3/g для gL =2.

(9.Б.13)

К / 1 / 2 2с!

— ~ (£. - е2) —

А До

В этом случае нормировочный коэффициент волноводной волны (9.21) составляет:

A2 =4Pq

В том случае, когда решетка сформирована на расстоянии О от сердцевины и имеет амплитуду модуляции к (смотрите рис. 9.Б. 1), константа связи в соответствии с (9.Б.6б) имеет вид:

D+h

Ює0єм Г 4 2 а -2кх,

8У

При этом с учетом (9.Б.13) и (9.Б14):

П ек

G =

4 П^(є, - є2 )

Это последнее выражение показывает, что эффективность брэгговского волновода определяется эффектом фотонного туннелирования (т. е. ос£~2к£))'

Пример----------------------------------------------------------------------------------------------------------------------------------------------------

Найдем произведение gL для волновода на основе ваАБ со следующими параметрами:

И, = 3,3, л2 = 3и£м=3

Л0 = 1 мкм, (1 = 0,5 мкм, В = 0,2 мкм и к = 0,1 мкм.

Волновое число аг составляет п/й или 6,28 мкм-1, при этом константа фотонного туннелирования к дается (9.Б. 13) и составляет (3,32 — Ъ2)Х12а = 8,63 мкм“1. В этом случае произведение gL определяется с использованием (9.Б. 16) или:

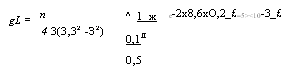Для получения величины gL порядка 1 нам необходима длина волновода 200г/ или 100 мкм.