НАЛАДКА ПРИБОРОВ И СИСТЕМ АВТОМАТИЗАЦИИ

Пеоеходные процессы

На вход звена, охваченного обратной связью (см. рис. 22, в), кроме сигнала возмущения подается сигнал с выхода звена. В точке, обозна­ченной крестиком, сигналы суммируются с учетом знака. Для регули­рования технологических процессов используют отрицательные об­ратные связи, в этом случае сигнал с выходом звена подается на вход со знаком, противоположным знаку возмущения.

Звенья АСР после охвата обратной связью меняют свои динами­ческие свойства (вид временных и частотных характеристик), поэтому положительные и отрицательные обратные связи широко используют при конструировании автоматических регуляторов для формирования их динамических характеристик.

Влияние обратных связей на динамические характеристики звень­ев рассмотрим на двух примерах: охвата безынерционного звена бе­зынерционной отрицательной обратной связью (рис. 27, а) и охвата

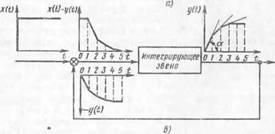
Рис. 27. Пример влияния отрицательной обратной связи на на временную характеристику звена: а — безынерционное звено, охваченное безынерционной отрицательной обратной связью, б — интегрирующее звено, охваченное единичной от­рицательной обратной связью

интегрирующего звена единичной (КуС = 1) отрицательной обратной связью (рис. 27, б).

Если в первом примере коэффициент усиления прямой цепи (рис. 27, а) равен лсх, а обратной к2, то рассогласование xv — xBX— —Хо. с- Из рисунка видно, что увых = xvkx (так как kl = увых/хр) и Хо. с = УъъпКг-

Отношение увых/квх есть коэффициент усиления всей схемы.

При конструировании регуляторов и решающих усилителей ана­логовых вычислительных машин коэффициент усиления прямой цепи выбирают очень большим {кх = оо). Следовательно, и кхк2 = оо В этом случае, не допуская большой погрешности, можно пренебречь единицей в знаменателе, т. е. для схемы с большим коэффициентом усиления в прямой цепи

Увых __ 1

*ВХ К1 к2 к2

В схемах с большим коэффициентом усиления в прямой цепи (1000 и более) коэффициент усиления всей схемы равен обратной величине коэффициентов усиления обратной связи.

Этот вывод распространяется на любое типовое звено, охваченное обратной связью. При достаточно большом коэффициенте усиления прямой цепи динамические свойства системы практически определя­ются только динамическими свойствами устройства обратной связи и не зависят от динамических свойств прямой цепи. Это свойство об­ратной связи широко используют при конструировании регуляторов.

Если к системе (рис. 27, б) приложить ступенчатое возмущение x(t) и предположить, что за время от t = 0 до t = 1 оно сохранится постоянным, ти на этом отрезке времени выходная величина y(t) будет нарастать с постоянной скоростью, обусловленной углом наклона а - Этот сигнал через обратную связь, попадая на вход звена, будет вы­читаться из сигнала возмущения. Предположим, что вычитаться из возмущения этот сигнал будет уже на отрезке времени t = 1—>-1 = 2. После вычитания выходной сигнал уменьшится. Значит, можно ут­верждать, что на отрезке /2 наклон y(t) тоже уменьшится.

На следующем отрезке времени t%-^ t3 в результате действия об­ратной связи входной сигнал уменьшится еще больше, а следователь­но, наклон y(t) тоже уменьшится. Пока на входе в звено будет даже самый незначительный сигнал, выходной сигнал интегрирующего звена будет расти. И только когда x(t) - y(t) — 0, сигнал на выходе перестанет расти. Полученная разгонная характеристика интегри­рующего звена, охваченного обратной связью, имеет вид разгонной характеристики инерционного звена.

Рассмотренные примеры наглядно показывают, что обратная связь существенно изменяет динамические характеристики элементарных звеньев.

АФЧХ звена, охваченного обратной связью, графически строит­ся следующим образом (рис. 28).

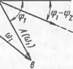
Рис. 28. Принцип построения АФЧХ охваченного отрицательной обратной связью

Для частоты <ох проводим под со - _f ответствующим этой частоте углом фх вектор иа АФЧХ звена. На ней откладываем ^4 (сог), т. е. строим АФЧХ звена для частоты Из точки на отрицательной веществен­ной полуоси, соответствующей зна­чению АФЧХ — 1 (в размерности АФЧХ), проводим прямую ав в конец вектора АФЧХ для Про­веденная таким образом прямая образует с вещественной полуосью угол ф2. Под углом, равным ф! —

— ф2, из начала координат проведем прямую об, которая совпадаете направлением вектора АФЧХ звена, охваченного обратной связью. Величина вектора АФЧХ звена, охваченного обратной связью, на­ходится как частное от деления вектора ов на вектор ав.

Следует обратить внимание на то, что включение обратной связи разворачивает вектор АФЧХ звена против часовой стрелки, так как фі “ф2<Іфі-

Динамические свойства звена, охваченного обратной связью, во многом совпадают с динамическими свойствами систем автоматическо­го регулирования. Изучение динамических свойств звена, охвачен­ного обратной связью, позволяет рассмотреть природу самовыравнивания (саморегулирования) и виды переходных процессов замкнутых систем регулирования.

Зная, как образуется АФЧХ звена, охваченного обратной связью, рассмотрим динамические ха­рактеристики интегрирующе­го звена после охвата его об­ратной связью для двух на­иболее характерных частот (о=0 (со0) и со-»- 00(0)00) (рис. 29). При ступенчатом возму­щении выходная величина интегрирующего звена неог­раниченно растет или, как иногда принято говорить, уходит в бесконечность. По­этому можно считать, что прямая, проведенная из точ­ки —1 в конец АФЧХ звена для частоты со0, будет парад­ом лельна вектору АФЧХ (рис. Рис. 29. АФЧХ интегрирующего звена, ™ . е угол го, = 90°охваченного отрицательной обратной связью для <о = 0 (о>0) (а) и со ->оо (оі»)(б) Отсюда вектор оа АФЧХ зве­на, охваченного обратной связью, будет выходить из начала коорди­нат под углом —ср2 = 90—90 = 0°, т. е. как и для инерционного звена, будет лежать на вещественной положительной полуоси.

Для частоты (а^А (со«) будет стремиться к 0, а следовательно, угол q>2, под которым вектор выходит из точки —1, будет стремиться тоже к нулю (рис. 29,6). Это значит, что вектор АФЧХ звена, охваченного обратной связью, будет выходить изначала координат под угломф,— —Фг = 90—0 = 90°. Как и в случае инерционного звена, вектор ов АФЧХ интегрирующего звена, охваченного обратной связью, при оо стремится к 90°.

Фактически такое изменение динамических свойств звена при охвате его обратной связью объясняется следующим образом.

На рис. 30,а приведены пример инерционного звена и соответст­вующая ему диаграмма прохождения сигнала, на которой видно, что при увеличении расхода на притоке GDp растет уровень Н жид­кости, увеличение уровня приводит к увеличению напора, с ростом напора увеличивается расход жидкости на стоке GCT • Рост GCT при­водит к уменьшению скорости роста уровня Н и является причиной того, что уровень сам устанавливается на новом значении (саморегу­лирование).

В диаграмме прохождения сигнала явно видна отрицательная обратная связь. Попробуем искусственно разорвать ее. Для этого установим на стоке насос, подача которого не зависит от напора. Подача такого насоса 6СТ не меняется с изменением уровня И (GCT = = const), поэтому и в диаграмме прохождения сигнала этой связи нет (рис. 30, б). Если теперь из диаграммы прохождения сигнала исключить напор, который после разрыва обратной связи нас не инте­ресует, то получим диаграмму прохождения сигнала, приведенную на рис. 30, в. Из этой диаграммы видно, что уровень Н зависит от рас­хода на притоке Gnp и от расхода на стоке GCT, действующих на уро-

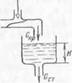
Рис. 30- Пример инерционного звена, образующегося в резуль тате охвата интегрирующего эвена внутренней обратной связью'- о — инерционное звено и диаграмма прохождения сигнала, б — разрыв внут­ренней обратной связи включением насоса на стоке и диаграмма прохождения сигнала, е — упрощенная диаграмма прохождения сигнала звена без само - выравннвания, г — временная характеристика звена без самовыравниваний

вень с разными знаками. Поэтому если Gnp — Gcr^= О, то уровень будет или расти, или уменьшаться с постоянной скоростью (рис. 30, г), как это имеет место в разгонных характеристиках интегрирующего звена.

Эффект действия рассмотренной нами внутренней обратной связи называется самовыравниванием на стоке. Существует самовыравнива - ние и на притоке, если уровень влияет на Gnp.

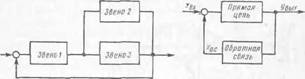
Обратной связью может быть охвачена и группа звеньев (рис. 31 ,а), соединенных и последовательно, и параллельно, и по смешанной

а.) 6)

Рис. 31. Смешанное соединение звеньев, охваченных отрицательной

обратной связью (а), и схечь включения тиг. овых звеньев в прямую и обратную связь (б)

соединенных и последовательно, и параллельно, и по смешанной

схеме. В этом случае необходимо построить характеристики группы звеньев без учета обратной связи, а затем характеристики всей систе­мы в целом.

Типовое звено может быть не только охваченным обратной связью, но и включенным в обратную связь (рис. 31,6). Для систем авторегу­лирования прямая цепь является каналом объекта регулирования (или сокращенно объектом регулирования), а звено в обратной свя­зи — регулирующим устройством, или регулятором. Меняя звенья в обратной связи (меняя регуляторы) и их качественные и количест­венные характеристики, можно получить различные характеристики системы звеньев. Рассмотрим временные характеристики систем, со­держащих в обратной связи различные типовые звенья (рис. 32).

Интегрирующее звено, охваченное обрат­ной связью с безынерционным звеном (рис. 32, а). Динамические свойства такой системы аналогичны инерционному звену. Временная характеристика является экспонентой. Коэффи­циент усиления системы равен обратной величине коэффициента уси­ления обратной связи к = 1//Со. с, а постоянная времени Т обратно пропорциональна произведению коэффициента интегрирующего зве­на є и коэффициента усиления обратной связи коС' Т Обратим внимание на тог факт, что при увеличении коэффициента усиления обратной связи к0.с коэффициент усиления системы и пос­тоянная времени системы Т уменьшаются. На рис. 33 показано, как С увеличением коэффициента усиления обратной СВЯЗИ (7С0.С1 </С0.с2 < </с0.сз) кривая по своей форме приближается к временной характе

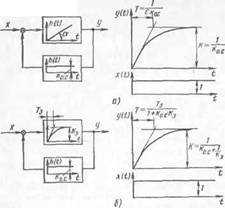
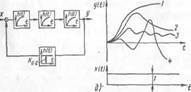
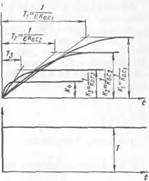
Рис. 32.

ристике безынерционного звена, так как при этом постоянная време­ни уменьшается (7;> Тг> Т$). Инерционное з вено, охваченное безынер­ционной обратной связью (см. рис. 32, б). Разгонная характеристика инерционного звена по форме не изменяемся после охвата ее безынерционной обратной связью, но, как и в первом случае (см. рис. 32, а), при неограничен­ном увеличении коэффициента уси - УМ ления обратной связи разгонная характеристика системы прибли­жается к характеристике безынер­ционного звена.

Безынерционное зве­но, охваченное безы­нерционной обратной с в я зыо (см. рис. 32, в). Харак­теристика звена после охвата об­ратной связью по форме не изменя­ется, но коэффициент усиления системы меняется в большом ди­апазоне в зависимости от величи­ны коэффициента усиления обрат­ной связи.

Интегрирующее зве­но с интегрирующим звеном в обратной свя - з и (см. рис. 32, г). В такой систе­ме при любом возмущении на вы­ходе возникают периодические не­затухающие колебания. Периодические колебания

сохраняются для любых значений & коэффициента передачи звена е3 и коэффициента передачи обратной связи е0.с; изменяются только частота и амплитуда колебаний. Здесь мы впервые сталкиваемся с основным недостатком систем с обратной связью. Эти системы при определенных условиях становятся генераторами периодических колебаний, т. е. эти системы склонны к самовозбуждению, к неустойчивости.

Изучению условий устойчивости замкнутых систем посвящена теория устойчивости, элементы которой будут рассмотрены в § 30.

Пример, приведенный на рис. 32, д, наиболее близок к условиям реальных систем авторегулирования. В примере рассмотрены три последовательных инерционных звена, охваченных безынерционной обратной связью с коэффициентом усиления Ко. с - При изменении Ко. с па выходе системы можно получать качественно отличные друг от друга временные характеристики — переходные процессы (кривые /, <?, 3, 4). При коэффициенте усиления, равном или близком к нулю, мы получим временную характеристику разомкнутой системы (кривая /). С увеличением коэффициента усиления кривые 2 и 3 становятся коле­бательными. При дальнейшем увеличении коэффициента усиления переходный процесс становится расходящимся (кривая 4), или неус­тойчивым. Переходные процессы, близкие к кривым 1 и 2, называются апериодическими (непериодическими), переходный процесс, близкий к кривой 3, — периодическим (или колебательным).

Из примера видно, что регулятор далеко не всегда стабилизирует процесс. При некоторых значениях коэффициента усиления обратной связи он может устойчиво работающую без регулятора разомкну­тую систему привести к расходящимся колебаниям.

Во многих технологических процессах, особенно химических, при отклонении регулируемых параметров за допустимые значения не только нарушается технологический процесс и ухудшается качество продукта, но и возникает опасность взрыва, поэтому обеспечение устойчивости системы авторегулирования обязательно для каждого налаживаемого регулятора. Это одно из главных требований к систе­мам авторегулирования, которое должно быть обеспечено качеством наладки.