КОНСТРУКЦИИ С ЗАПОЛНИТЕЛЯМИ ИЗ ПЕНОПЛАСТОВ

Оптимальные параметры панели

А. Пластины в условиях цилиндрического изгиба

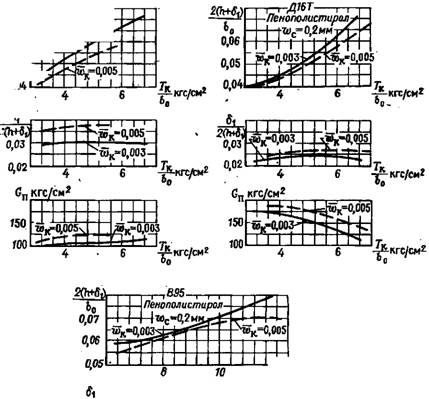
На рис. 3.18 и 3.19 приведены графики оптимальных пара­метров, построенные по методике, описанной в § 1 этой главы, для пластин, работающих на продольное равномерное сжатие в условиях цилиндрического изгиба (стержни, бесконечно широ­кие пластины). Пластины имеют одинаковые внешние слои и за­полнитель из. неармированного (рис. 3.18) и армированного (рис. 3.19 и 3.3) пенопласта. Материал внешних слоев и арми­рующих ребер и марка пенопласта показаны на графиках. По оси абсцисс отложены значения параметра нагружения — отно­шение критической нагрузки Тк на единицу ширины пластины к расчетной длине пластины Ьо=мЬ. Здесь Ь — размер пластины в направлении сжатия. Для пластины со свободно опертыми кром­ками v=l, для пластины с защемленными кромками v=0,5. Гра­фики построены для различных значений параметров начального искривления пластины wv=wK/b0 и начальной волнистости внеш­них слоев wc (см. п. 5 § 2). По заданным значениям TJb0, wK и Wc по графику рис. 3.18 определяют оптимальные значения тол­щины внешних слоев 61,2, толщины слоя 2h и плотность уп запол­нителя.

В случае армированного пенопласта (см. рис. 3.19) минимуму веса панели соответствует использование пенопласта, плотность которого меньше, чем минимальная плотность для данного клас­са пенопластов, выпускаемых промышленностью в настоящее время. При расчетах графиков для пенопласта ФК-20 было при­нято уп=0,1 г/см3,-для пенополистирола Yn=0,05 г/см3. По графи­кам находят значения 63/64. Значения бз и 64 определяют из усло­вия устойчивости ребер армировки (см. п. 3, Б).

Б. Пластины и пологие оболочки При различных условиях опирания

Графики оптимальных параметров, построенные для случая бесконечно широких пластин (п. 1 этого параграфа), можно ис­пользовать для различных условий опирания плоских и криво­линейных панелей при помощи следующего приема.

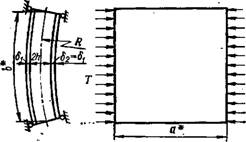
Пусть, например, требуется найти оптимальные параметры продольно сжатой свободно опертой по контуру прямоугольной в плане цилиндрической панели (рис. 3.20). Размеры этой панели в плане, материал ее, параметры, характеризующие начальные технологические несовершенства, и значения нагрузок заданы. Заменим заданную цилиндрическую панель продольно сжатой, свободно опертой по нагруженным кромкам бесконАно широкой пластиной, у которой^ за исключением размеров в плане, все ге­ометрические параметры, а также упругие и прочностные'пара - - гетры ее внешних слоев и заполнителя такие же, как и у задан­ной. Размер Ъ бесконечно широкой пластины в направлении сжа­тия будем подбирать так, чтобы критические нагрузки общей устойчивости Тк на единицу ширины у заданной панели и заменя­ющей ее пластины в предположении идеализированной упругой работы конструкции были одинаковы (эти нагрузки Тк определя­ются по формулам и графикам п. 1 этого параграфа).

Оптимальные параметры будем находить для этой заменяю­щей пластины и считать, что они соответствуют заданной панели. При этом будем считать, что у обеих панедей одинаков пара­метр Wv, характеризующий начальное кососимметричное 'искрив­ление и определяющий величину поперечной силы, возникающей при продольном сжатии панели Подбор ведется методом после­довательных приближений. В первом приближении для обеих панелей, заданной и заменяющей ее, примем модули сдвига за­полнителя в направлении сжатая Gc =',<», при заполнителе из ар­мированного пенопласта Gc= GIZ, при заполнителе из неармиро­ванного панопласта Gc = Gn. Зададимся размером H или 6i и исходя из равенства критических нагрузок общей устойчивости, используя соответствующие формулы, найдем размер Ь заменяю­щей пластины через известный размер а* заданной панели (для размера заданной панели вводим здесь обозначение а*, чтобы не смешивать эту величину с размером Ь заменяющей пластины). Напомним, что размер панели в направлении сжатия для беско­нечно широкой пластины (см. рис. 3.2) в разд. 1 обозначен через Ь, для прямоугольной панели — через а.

Теперь для заменяющей пластины с найденным размером b и параметром wv определим оптимальные параметры по графи­кам рис. 3.18, 3.19. Будем считать эти параметры параметрами проектируемой панели и найдем во втором приближении размер Ь, а также параметры H и 6j заменяющей пластины, полагая, что модуль сдвига заполнителя этой пластины равен найденному в первом приближении значению. Дальнейшие приближения, если они нужны, могут проводиться по той же схеме, пока. исходное и полученное значения модулей сдвига заполнителя, H и других параметров панели не окажутся близкими (пример такого расче­та дан ниже).

Ребрами

В. Пластина на подкрепляющем слое с переменным на толщине модулем упругости

При равномерном продольном сжатии однослойной пластинъ (с толщиной 6i и упругими параметрами Е и щ и плотностью Yi) лежащей на подкрепляющем слое большой толщины (см рис. 3. 15), этот слой в некоторых случаях выгодно, с точки зре­ния экономии массы, изготовить из пенопласта, плотность кото­рого (а следовательно, и модуль сдвига) убывает по толщине пс мере удаления от поверхности склейки с пластинок

Если закон изменения модуля подкрепляющего слоя по тол­щине имеет вид

Ес — Еф~тг,

А плотность материала подкрепляющего слоя линейно связана - модулем упругости, где ус=сЕс;

Е0 — значение модуля у поверхности склейки пластины с под крепляющим слоем (при 2=0) (см. рис. 3.15); С — коэффициент пропорциональности, то оптимальные пь раметры находятся по формулам

, = 0,2*1/.

С » '

Значение коэффициента с см. в гл. I. Для пенопласта ПС-1

С = 0Л7- 10-в—.

См

Формулы применимы в случае подкрепляющего слоя достаточ­но большой ТОЛЩИНЫ, 30.

61