Гранулирование

Тепломассообмен

Особенности формирования гранул и скорость их роста в значительной мере определяются характером тепломассообмена в псевдоожиженном слое, условиями взаимодействия между каплями диспергированного раствора или плава и частицами.

Удаление влаги и кристаллизация гранулируемого вещества происходят в условиях взаимодействия капель с сушильным или охлаждающим (для плавов) агентом и отдельными грану­лами.

Первая попытка анализа теплообмена между жидкостью и гранулой предпринята В. Ф. Волковым (цитируется по [21]), который рассчитал испарение пленки раствора, полностью охва­тывающей гранулу, при условии совмещенного подвода тепла: кондукцией от гранулы и конвекцией от ожижающего агента. Толщину пленки определяли экспериментально (окунали гра­нулу в раствор, давали стечь избытку последнего и после обра­зования пленки замеряли ее толщину). Решая упрощенную за­дачу теплообмена шара со средой с постоянной температурой, получили критериальную зависимость:

Nu,*=j4(2ЯтАг) [(Г«-ГМд)/{Гп. с-Г„+д)1+Ши„„, (4.35)

где?.т, ?.г — теплопроводность твердого материала и газа; Tr, 77п-л, Тп. с — температура поверхности гранулы, пленки, псевдоожиженного слоя; Nu8$, Nuhcct — число Нуссельта, эффективное и рассчитанное по уравнению Нестерен­ко [91]; Ві*=а/?ДТ — критерий БИО (а — коэффициент теплоотдачи; R — ра­диус гранулы); А, В — эмпирические константы.

В соответствии с формулой (4.35) 60—70% тепла на испаре­ние влаги в пленке поступает от нагретых гранул. Принимая во внимание, что капля не мгновенно растекается по поверхности гранул, следует рассматривать, как это сделано в работе [89], нестационарный процесс растекания испаряющейся капли по поверхности нагретой гранулы. Естественно предположить, что в зависимости от соотношения времени испарения и времени растекания капли будет изменяться механизм гранулообразо - вания. При очень быстром подводе большого количества тепла влага удаляется из капли значительно скорее, чем она успева­ет растечься по грануле. При недостатке тепла, подводимого для испарения влаги из данной капли, капля может полностью покрыть гранулу, которая приобретает повышенную влажность. Очевидно, что механизм гранулообразования в этих случаях бу­дет зависеть не только от скорости удаления влаги, но и от ско­рости растекания пленки по поверхности гранулы, что, в свою очередь, определяется физико-химическими свойствами грану­лируемого вещества.

Интересны результаты экспериментальных исследований [89] процесса испарения капель раствора на поверхности гра­нул различных размеров при варьировании первоначальной температуры гранулы (trp). При /гР=135°С происходит некото­рое растекание капли, медленный ее нагрев и испарение влаги, в процессе которого наблюдается плавное снижение температу­ры гранулы. При этом максимальная разность начальной и те­кущей температур (Д*) составляет 5 °С. После испарения рас­твора образуется прочный нарост, профиль которого соответст­вует профилю поверхностной пленки (растекшейся капли).

С повышением температуры толщина прочной подложки и размеры отдельных наростов уменьшаются. При frp=350°C происходит еще более интенсивное кипение (время испарения 2—3 с, А£=40°С). Вновь образованная поверхность изрыта трещинами и непрочно прилегает к грануле (наросты в виде пылевидных крупинок).

При соотношении размеров капли и гранулы 1 : 1 происходит полное обтекание гранулы для всех исследованных температур trp. При температуре frp<200°C образуется тонкая твердая пленка, избыточное количество раствора стекает с гранулы.

Таким образом, характер гранулообразования во многом за­висит от количества тепла, аккумулированного гранулой, т. е. от ее теплосодержания. С увеличением последнего в исследо­ванных условиях рост гранул замедляется, поскольку нанесен­ная пленка имеет непрочные связи с гранулой. При диспергиро­вании в зоне орошения не раствора, а пульпы, имеющей более высокую температуру, чем гранула, в процессе испарения влаги из пленки происходит кристаллизация дополнительного количе­ства твердой фазы. Это приводит к уменьшению сил сцепле­ния с гранулой. Следовательно, возможны условия, при кото­рых замедление роста гранулы по поверхности происходит вследствие понижения температуры гранулы.

Размеры и форма нанесенной на гранулу пленки зависят от текучести капли, т. е. от вязкости и поверхностного натяжения раствора, соотношения размеров капли и гранулы, шероховато­сти и смачиваемости поверхности последней.

Следует заметить, что изложенные выше выводы получены на основе анализа взаимодействия единичных капель и гранул. В реальном процессе это взаимодействие осложнено возможно­стью одновременного контакта гранулы с несколькими капля­ми, передачи части жидкости с одной гранулы на другие при их столкновении, под действием центробежной силы при вра­щении гранул, при обдуве их ожижающим агентом и т. п. По­этому знание особенностей взаимодействия единичных капель и гранул хотя и помогает выявить факторы, влияющие на про­цесс гранулообразования, но не дает однозначного объяснения закономерностей роста гранул в псевдоожиженном слое и не позволяет описать процессы тепломассообмена, протекающие при гранулировании.

Математическое описание процесса сушки зернистых мате­риалов во взвешенном слое включает совместное рассмотрение внутренней задачи тепломассообмена — внутри капиллярно-по­ристого тела — и внешней задачи тепломассообмена поверхнос­ти влажного тела и сушильного агента. Сушка жидкости имеет специфические особенности, связанные с кристаллизацией твер­дой фазы в процессе формирования гранул.

Дифференциальные уравнения тепломассопереноса при суш­ке капиллярно-пористых тел имеют вид:

ди/д тс=a'V2«+a'6V2/,

dtldxc=aV4+z(rilcv) (ди/дтс), (4.36)

где и — влагосодержание; гс — среднее время пребывания гранул в слое; а, а'Ь — коэффициенты температуро - и потенциалопроводности (они посто­янны, если расчет производить по зонам, на которые разбивается тепло - и массообмен, т. е. для каждого интервала и и t); е — критерий фазового превращения; Гі — теплота испарения; ср — теплоемкость гранул.

Как уже отмечалось, при гранулировании капли раствора распределяются тонкой пленкой на поверхности гранул, нахо­дящихся в псевдоожиженном слое. Имея в виду высокую ин­тенсивность процесса сушки, можно предположить, что испаре­ние влаги в поверхностном слое гранул, а следовательно, ко­эффициент внутреннего испарения е, градиент влагосодержа - ния Vm и изменение влагосодержания во времени ди/д-сс внут­ри гранулы близки к нулю. Таким образом, уравнение массо - переноса внутри гранулы теряет смысл, а уравнение теплопере - носа имеет вид уравнения Фурье —Кирхгофа:

dtldxc—aS72t. (4.37)

Краевое условие для процесса сушки жидкости в псевдо­ожиженном слое представляет собой уравнение теплового ба­ланса одной гранулы за бесконечно малый промежуток вре­мени:

(pd/б) (<3(7дтс)п+сс(/с — <п) = К(dt/dx),,+ (prf/6) г(ди/дтс) п, (4.38)

где d — эквивалентный размер гранул; і — теплосодержание гранулы; а — коэффициент теплоотдачи; tc, t„ — температуры ожижающего (сушильного) агента и поверхности гранул; ?.м — коэффициент теплопроводности мате­риала гранулы; х — текущий линейный размер гранулы.

Особенностью рассматриваемого процесса является наличие дополнительного источника тепла в поверхностном слое грану­лы (теплоты фазового превращения), которое учитывается пер­вым слагаемым в левой части уравнения (4.38). Второй член левой части уравнения учитывает теплообмен между поверхно­стью гранулы и газом. Первое и второе слагаемое в правой части уравнения характеризуют количество тепла, отводимого от поверхности внутрь гранулы и расходуемого на испарение влаги.

В результате преобразования системы дифференциальных уравнений (4.37) — (4.38) методами теории подобия получено выражение:

£=ы/цп=([Рг> Re> Gu.'Fo, Ли, Ко(<эк — tr)l(/п — Ал), Хм/ЭД. (4.39)

где и, и„ — влагосодержание гранул н пульпы; Рг, Re, Gu, Fo, Au, Ко — числа Прандтля, Рейнольдса, Гухмана, Фурье, автотермичности, число Кос - совича.

Выражение (4.39) при рассмотрении конкретных условий проведения процесса гранулирования может несколько упрос­титься. Так, если сушильным агентом является воздух, то влия­ние Re и ХмА-г постоянно и учитывается постоянным коэффици­ентом уравнения. При небольших разностях температур слоя и

поверхности гранул числа Ко и ((эк—tr)/(t„—tCJ]) принимают очень большие значения и процесс становится автомодельным к этим числам.

При сушке растворов, охлаждении плавов в псевдоожижен­ном слое происходит кристаллизация твердой фазы на поверх­ности гранул, что сопровождается выделением тепла. Это изме­нение теплосодержания на поверхности гранулы учитывается числом автотермичности:

Аи=Д ЦгЫ], (4.40)

где Ді — количество тепла, выделяющееся при кристаллизации пленки рас­твора на поверхности гранулы; гАи — количество тепла, подводимое для испарения влаги; г — теплота испарения воды; Аи=и„—щ и„, и — влагосо - держанне соответственно пульпы и гранулы.

Установлено, что при гранулировании пульп изменение чис­ла Аи незначительно и может быть учтено постоянным членом в уравнении (4.39).

Таким образом, процесс сушки растворов, пульп или плавов в псевдоожиженном слое определяется в основном числами Аи, Re, Gu, Fo. Степень их влияния на влагосодержание продукта зависит от его свойств и определяется экспериментально. В ка­честве примера приведены некоторые эмпирические уравнения [21];

а) гранулирование аммиачной селитры:

lg £=— 0,48- 105FoRe,’72Gu°'7Au-1’* (4-41>

при Fo=22—270, Re=83—160, Gu = 0,07—0,14, Au = 0,47—1,94;

б) гранулирование двухслойных удобрений карбамид —ам­мофос:

£=0,lGu-°-66Fo-°-61> (4.42)

при Gu = 0,080—0,125; Fo=55—602, Re=3,5-106;

в) гранулирование сложных удобрений типа нитроаммофос­ки:

Зависимости (4.43) и (4.44) справедливы при изменении па­раметров в пределах: QP. a/Qn=l, l—2,3, Fo = 54—240, Gu = 0,07— 0,14.

Приведенные уравнения (4.41) — (4.44) позволяют рассчи­тать относительное влагосодержание готового продукта и реко­мендовать режимы ведения процесса для получения гранул за­данной влажности.

На тепломассообмен, а следовательно, и на рост гранул су­щественное влияние оказывает структура псевдоожиженного слоя, в частности порозность, степень однородности, интенсив­ность перемешивания в плотной и разреженной зонах.

Расширение слоя при псевдоожижении. Известно, что высота псевдо­ожиженного слоя с увеличением скорости ожижающего агента возрастает, т. е. слой расширяется. Высота рабочей зоны Нр при этом рассчитывается на основании закономерностей расширения псевдоожиженного слоя. Условия расширения псевдоожиженного слоя и его структура (однородная или неод­нородная) определяются характером движения ожижающего агента

Расширение слоя при однородном характере движения ожижающего агента (без образования газовых неоднородностей, т. е. пузырей) начинается прн условии Шр>ш0 (скорости—рабочая и начала псевдоожижения). Прн этом скорость движения ожижающего агента в каналах между частицами всегда равна скорости стесненного витания. Увеличение рабочей скорости ожижающего агента wp приводит к увеличению порозности еп до тех пор, пока скорость в каналах не достигнет скорости витания ш„. Уменьшение скорости ожижающего агента адр приводит к снижению порозности е„, и следовательно, высоты слоя.

Установлено, что прн однородном характере движения ожижающего агента справедливо следующее выражение:

/Ы1-е0) = //р(1-е„), (4.45)

где Нв — высота неподвижного слоя; Нр — рабочая высота псевдоожижен­ного слоя; е0 — порозность неподвижного слоя; е„ — порозность псевдоожи­женного слоя.

При этом порозность псевдоожиженного слоя вполне удовлетворитель­но (с погрешностью, не превышающей 10—15%) может быть рассчитана по формуле Тодеса:

еп= [(18Re+0,36Re2)/Ar]°.2‘, (4.46)

Для псевдоожиженного слоя с неоднородным движением ожижающего агента особенности расширения являются следствием более сложных явле­ний. Такой слой характерен для систем газ — твердые частицы, где ожижаю­щий агент движется как в каналах между частицами, так н в виде пузы­рей. Формирование пузырей, их движение и выход из слоя сопровождаются пульсациями давления. С ростом скорости ожижающего агента увеличива­ется количество газа, проходящего в виде пузырей. В соответствии с двух­фазной теорией, количество газа, проходящего в виде пузырей, равно коли­честву газа сверх необходимого для минимального псевдоожижения, т. е.

Qny3 = (wp—w0)F, (4 47)

где F — площадь сечения аппарата.

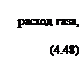Обозначив скорость подъема пузырей через v„, получим проходящего в виде пузырей:

Qny3=(FHp-FHc)l(Hlv„).

Приравнивая уравнение (4.47) и (4.48), получим:

HpIHD=vJ(vn — Wp+Wo). (4.49)

Следовательно, расширение неоднородного псевдоожиженного слоя оп­ределяется количеством газа, подведенного сверх необходимого для мини­мального псевдоожижения и проходящего в виде пузырей.

Для определения средних значений высоты Нср неоднородного псевдо­ожиженного слоя Н. Л. Шаховой с сотрудниками получены следующие эм-

лирические уравнения:

//cp/Wo=5,6Re°-76Ar-0-37 для Яо>0,2 м, (4.50)

WCp/Wo=cRe°'76Arm для Я0<0,2 м. (4.51)

Значения сит могут быть определены из следующих выражений:

с= 126Я0-овг, (4.52) т—— 0,63Яо“°'. (4.53)

Структура неоднородного псевдоожиженного слоя. Структу­ра неоднородного псевдоожиженного слоя локально неустойчи­ва. Это обусловлено тем, что неоднородное псевдоожижение, существующее, как правило, в реальных системах газ — твер­дая фаза, сопровождается интенсивным барботажем пузырей, образованием и распадом агрегатов частиц в плотной фазе слоя.

Нестационарность движения газовых пузырей и случайный характер их взаимодействия во многом ограничивают возможно­сти детерминированного подхода к описанию структуры псевдо­ожиженных систем.

Ранее Н. А. Шаховой было показано, что газовые пузыри в псевдоожи­женном слое образуются в результате пульсационного отрыва струй, исте­кающих из отверстий газораспределительного устройства. Отрыв струн про­исходит вследствие ее сжатия в среде большой плотности (плотность псев­доожиженного слоя значительно превышает плотность газовой струи). Сжа­тие струн приводит к повышению давлення в образующемся факеле. Когда давление достигает определенного значення, происходит разрыв струи и - об­разуется одиночный газовый пузырь. Если отверстия в газораспределитель­ной решетке достаточно отдалены друг от друга, коалесцениия пузырен в момент их образования отсутствует, н образуются пузыри одинакового размера. В случае слияния факелов в момент их отрыва при истечении стесненных струй вероятнее всего формирование неодинаковых пузырей, размер которых можно характеризовать некоторой плотностью распреде­ления.

Таким образом, неоднородность псевдоожиженного слоя предопределена уже начальным распределением зарождающихся пузырей по размерам, кото­рое зависит не только от аэродинамических характеристик истечения струй, но и от конструктивных параметров газораспределительного устройства.

В общем случае для единичного пузыря массой т, не встречающего на своем пути газовых объемов, можно записать следующее уравнение дви­жения:

mdvn/dt=P — a+mg, (4.54)

где t'n—скорость пузыря; Р — сила давления на пузырь; о — сила внутрен­него трения; g — ускорение свободного падения.

Полагая, что газовый пузырь имеет сферическую форму н сопутствую­щая эффективная масса окружающего пузырь слоя равна половине вытес­ненной им массы, И. Ф. Дэвидсон и Д. Харрисон [92] приводят следующее уравнение восходящего движения пузыря:

Рп. с Vg= d (1 /2рп. с Kdz/dT) /dT, (4.55)

где V — объем пузыря; р„.с — плотность псевдоожиженного слоя; г — высота подъема пузыря от точки зарождения.

Известно, что реальный газовый пузырь имеет форму, отличную от сфе­рической, и по мере подъема либо увеличивается в размерах за счет коа - лесценции, либо разрушается на меньшие объемы плотными неоднородностя­ми (пакетами) .

Поэтому аналитическое описание движения пузыря возможно лишь на участках между столкновениями двух пузырен. Среднее число слияний пу-

7—631

зырей по высоте псевдоожиженного слоя можно оценить на основании сле­дующих экспериментальных данных. Частота образования пузырей для слоя стеклянных шариков d=0,8 мм в диапазоне чисел псевдоожижения 1,0< tt7<4,0 составляет 18—30 с-1. Частота же выхода пузырей на поверх­ность слоя как для лабораторных, так и для промышленных аппаратов обычно лежит в интервале 2—10 с-1. Это означает, что в среднем при высо­те слоя 0,2—0,5 м происходит 3—6 последовательных слияний, приводящих к ступенчатому укрупнению пузырей (рнс. 4.5).

Рост пузыря на участке Дz, можно описать уравнением

&(mi&zl&x)l&%= (dmildi)g — АР, (4.56)

где т—сопутствующая пузырю эффективная масса псевдоожиженного слоя на участке Дг,-.

Решение этого уравнения на всех участках возможно при следующих краевых условиях:

т=т0, г=г0, т=т0

Т = Т;, Z = Zj, m—nti.

Состояние г=то, z=z0, т—то соответствует моменту и уровню образо­вания первичного пузыря, зародившегося в результате отрыва факела струи. В первом приближении можно считать, что в точках слияния (zb z2, z3, ..., z.) происходит скачкообразное укрупнение пузырей без потерь газа в объеме псевдоожиженного слоя.

Если отрыв струй и коалесценция пузырей в плотной зоне псевдоожи­женного слоя вызывает микропульсацин давления, то выход пузырей на по­верхность слоя сопровождается макропульсациями давления, так как при этом в надслоевое пространство выбрасываются крупные пакеты частиц.

Если предположить, что частоты выброса пакетов частиц совпадают с частотами макропульсацнй давления в слое, то в этом случае можно объ­яснить причину и дать определение степени неоднородности псевдоожижен­ного слоя.

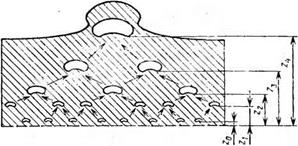
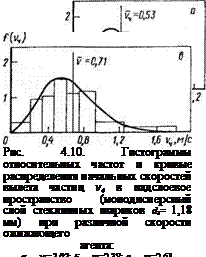
Гистограмма относительных частот выброса пакетов частиц из плотной фазы слоя стеклянных шариков йэ=1,18 мм при скорости ожижающего аген­та (воздуха) 1,21 м/с приведена на рис. 4.6.

Средняя частота периодов макропульсаций давления (выброса пакетов частиц) убывает с увеличением скорости ожижающего агента (рис. 4.7), в то время как частота микропульсаций при этом увеличивается. Это озна­чает увеличение степени неоднородности псевдоожижеииого слоя: большая часть газа проходит в виде пузырей.

Приведенные данные находятся в качественном соответствии с результа­тами экспериментального исследования (рис. 4.8) [93] (на частицах разме­ром d3= 2,5; 3,6; 4,3 мм) зависимостей параметров распределения скорости ожижающего агента коррелированных с пульсациями гидравлического сопро-

у, с-' 6 г

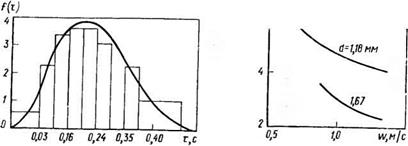Рис. 4.7. Зависимость средней частоты Y выброса пакетов частиц от скорости
ожижающего агента w стеклянных шариков различного диаметра d

тивления псевдоожиженного слоя, от скорости ожижающего агента (область чисел псевдоожижения после W=2—2,5). Экстремальный характер приведен­ных зависимостей подтвержден также в работе [94].

Степень неоднородности псевдоожиженного слоя обычно характеризует­ся отношением средней величины макропульсаций давления к среднему пере­паду давления в слое »Н=АР7АР.

Однако этот параметр скорее характеризует не степень неоднородности, а лишь указывает на наличие неоднородностей в системе. На наш взгляд, мерой степени неоднородности данной псевдоожиженной системы может служить параметр Т):

r = n/v, (4.57)

где п — частота микропульсаций (зарождения пузырей); v — частота макро­пульсаций давления (выброса пакетов в надслоевое пространство).

При п= гетерофазная система газ — твердые частицы может считать­ся однородной (ц= I). Такое состояние системы наблюдается в момент на­чала псевдоожижения, когда пузырьки газа, образовавшиеся вблизи газорас - пределителей решетки, не сливаются по мере их подъема и выходят на по­верхность слоя с той же частотой.

При n2>v псевдоожиженный слой становится неоднородным вследствие коалесценции пузырей н выхода на поверхность слоя крупных газовых не­однородностей и пакетов частиц.

Рис. 4.8. Зависимость ширины спектра изменения скорости ожижающего аген-
та аг (а) н наиболее вероятной частоты wor (б) от скорости ожижающего
агента т для частиц силикагеля различного диаметра

Рис. 4.9. Принципиальные схемы
(а—в) образования разреженной зо-
ны неоднородного псевдоожиженного
слоя:

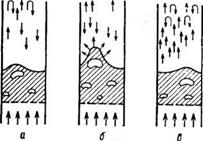а — формирование пакета частиц; б — вы-
ход пакета из плотной зоны слоя; в — рас-
пад пакета »а отдельные частицы и фор-
мирование следующего пакета

Структура разреженной зоны (надслоевого пространства) неоднородного псевдоожиженного слоя. Базируясь на изложен­ной выше модели структуры неоднородного псевдоожиженного слоя, объясняющей механизм движения газовых пузырей и природу пульсаций давления в слое, можно предложить следу­ющую модель образования разреженной зоны. На рис. 4.9 изо­бражена принципиальная схема образования разреженной зоны неоднородного псевдоожиженного слоя. Состояние слоя в зоне а определяется формированием пакета частиц, в зоне б — момен­том выхода пакета из плотной зоны слоя, в зоне в — распадом данного пакета на отдельные частицы и формирование следую­щего.

Для характеристики структуры разреженной зоны можно выбрать какую-либо статистическую модель распределения па­кетов по начальным скоростям их выброса из плотной зоны слоя. Такая модель в общем виде отражает энергетическое со­стояние неоднородного псевдоожиженного слоя на границе плотный слой — разреженная зона.

Экспериментальные исследования структуры разреженной зоны псевдоожиженного слоя [95] проведены методом кино­съемки с использованием моно- и полидисперсных слоев, харак­теристика которых дана в табл. 4.1.

В результате обработки экспериментальных данных для различных со­стояний монодисперсных систем получены следующие зависимости для пара­метров распределения пакетов по начальным скоростям их выброса:

/ Ю = iYV+1/Г (у + 1) «п) (HnM,)-<v+2)exp (—у«п/Чп), (4.58)

т«іИ>-.Агв-“ (4.59)

7n = 0,09ArMs |g w, (4.60)

где Г(к+1) —гамма-функцня Эйлера.

Уравнения (4.59) и (4.60) получены для следующего диапазона иссле­дованных параметров слоя:

1,3<1Г<7,3; 2,9- 103<Ar«s4,4-105.

Полученные обобщения для параметров эмпирического распределения частиц по начальным скоростям выброса их из плотной фазы слоя позволя­ют проводить количественную оценку спектра скоростей частиц в диапазоне исследованных параметров псевдоожиженного слоя.

Дальнейший анализ гистограмм относительных частот распределения случайной величины скорости вылета частиц v4 позволил установить, что для различных состояний монодисперсных псевдоожиженных слоев они удовлет­ворительно описываются распределением, аналогичным распределению Макс­велла:

/(и ч) = (mJ2nkw)i/2exp (— m4v42l2kw)4nv42, (4.61)

где тч — масса частицы; w — скорость ожижающего агента; v4 — скорость движения частицы в надслоевом пространстве; k — кинетический параметр распределения.

На типичные гистограммы, изображенные на рис. 4.10, нанесены кривые распределения (4.61).

F(vJ f(Kj

Тот факт, что рассматриваемая статистическая система (разреженная зона неоднородного псевдоожиженного слоя), содержащая большое число частиц, характеризуется распределением модуля скорости частиц, аналогич­ным распределению по скоростям движения молекул идеального газа, сви­детельствует о термодинамической общности обеих систем.

Эта аналогия, как справедливо сообщается в работе [96], базируется на определенном сходстве энергетических состояний рассматриваемых систем.

Подобно тому, что мерой кинетической энергии молекул газа является температура t, мерой интенсивности движения частиц в разреженной зоне псевдоожиженного слоя можно считать модуль скорости ожижающего агента.

Наряду с распределением частиц по начальным скоростям их вылета (4.61) можно получить распределения по импульсам и энергиям. Вводя в распределение (4.61) новую переменную р = m4v4, получим распределение частиц по импульсам:

f(p) = (1/2лтч^кі)3/2ехр(— р/2тчкш)Апрг. (4.62)

Выражая импульс через энергию частицы р= (2т„в)1/2, найдем распре­деление частиц разреженной зоны по начальным энергиям в момент их вы­лета из плотной зоны псевдоожиженного слоя:

((е)=2/[я(Лш)а],/2 ехр(— e/kw)eu2. (4.63)

Проанализируем характерные величины распределения (4.61).

Наиболее вероятная скорость вылета частиц гч", выражаемая максиму­мом кривой распределения скоростей, т. е. f'(v4)— 0 будет

очр=(2 kwlm4)in. ' (4.64)

Средняя начальная скорость вылета частиц определится как

on

v4~ I* vj (v4) dn4 = (8to/M!4)i/!. (4.65)

0

Из уравнения (4.65) можно выразить кинетический параметр распреде­ления:

к = тчс2ч/2,56ш. (4.66)

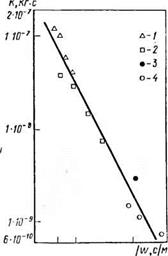
Рассчитывая кинетический параметр распределения (4.61) по формуле (4.66) для частиц различных моноднсперсных слоев при различных состоя­ниях псевдоожиженного слоя, получим зависимость вида /г = [(го). На рис. 4.11 изображена экспериментальная зависимость кинетического парамет­ра k от скорости ожижающего агента. Как видно из рисунка, опытные точ­ки вполне удовлетворительно аппроксимируются степенной зависимостью

k=Awn. (4.67)

Для моноднсперсных слоев в диапазоне скоростей ожижающего агента (0,3< ю <1,3 м/с) /1 = 3,16-Ю”8; п=4.

Решая совместно уравнения (4.66) и (4.67) получим эмпирическое выра­жение для расчета средней начальной скорости вылета частиц:

сч = 8,1 10“8и^/тч. (4.68)

Величина k определяет соотношение между средней энергией отдельной частицы тчсч2/2 и модулем скорости ожижающего агента.

Экспериментальные данные показали, что в разреженной зоне монодис- персного псевдоожиженного слоя силы взаимодействия между частицами пренебрежимо малы. Наибольшие отклонения экспериментальных точек от зависимости (4.67) наблюдаются для малых чисел псевдоожижения. Учиты­вая пакетный характер выброса частиц и, следовательно, некоторую устой­чивость пакетов при малых скоростях обтекания их газовым потоком, мож-

Рис. 4.11. Зависимость кинетического пара-
метра распределения k от скорости ожи-
жающего агента w для моноднсперсных
слоев:

1 — стеклянные шарики, d5 = 1,67 мм; 2 — стеклян
ные шарики, d3 = I,18 мм; 3 — шарики полистиро-
ла, d3 — 0,895 мм; 4 — стеклянные шарики, d.=
=0,315 мм

но отметить влияние стесненности на ско­рость движения частиц. С увеличением ско­рости ожижающего агента пакеты теряют свою устойчивость в надслоевом простран­стве, уменьшается объемная концентрация частиц, и их взаимодействие друг с дру­гом становится пренебрежимо малым. Сред­нестатистическое отклонение экспернмен тальных точек для зависимости k=f(w) не превышает 15%.

Ввиду того что кинетический пара­метр k распределения (4.61) является лишь функцией энергетического состояния псев­доожиженной системы (модуля скорости ожижающего агента), можно пред­положить, что уравнение (4.67) будет справедливо и для полидисперсных псевдоожиженных слоев.

С этой целью введем понятие массы отдельной частицы такого монодне - персного слоя, который но своему энергетическому состоянию эквивалентен полидисперсному слою прн данной скорости псевдоожижения, т. е. будем считать энергетически тождественными две системы (моно - и полидисперс ную), если они дают один н тот же спектр начальных скоростей вылета частиц.

Эквивалентную массу частицы полидисперсного слоя тэ будем опреде­лять по формуле

тэ = 2,566ш/Лі, (4.69)

где k — параметр, определяемый из уравнения (4.67); Т:ч — среднее значение начальной скорости вылета частиц, соответствующее данному состоянию по - лиднсперсного псевдоожиженного слоя.

Заметим, что сложная смесь частиц широкой степени полиднсперсности в момент начала псевдоожижения может быть охарактеризована двумя про­стейшими моделями моноднсперсных слоев: во-первых, слоем частиц разме­ром da, который при скорости газа w=wc дает такое же распределение на­чальных скоростей вылета частиц, какое имеет полидисперсный слой при этой скорости ожижающего агента; и, во-вторых, монодисперсным слоем частиц размером е!0, скорость начала псевдоожижения которого совпадает со значени­ем w0. При этом первый эквивалентный монодисперсный слой находится в состоянии развитого псевдоожижения, а второй — в критическом состоянии потери устойчивости.

Очевидно, отношение размеров частиц этих моноднсперсных слоев мо­жет служить характеристикой полиднсперсности моделируемого слоя:

jl=d3/do. (4.70)

При da—>-0 и, следовательно, при я—<-0 распределение начальных ско­ростей вылета вырождается для состояния слоя w — vs и, что характерно лишь для монодисперсного слоя. Предельным значением характеристики полндис - персности может быть я—*-1. В этом случае dB—>-dc, что предполагает зна­чительную ширину спектра размеров частиц, составляющих полидисперсный слой. Для представленной на рис. 4.12 полидисперсной псевдоожиженной си­
стемы гранулированного суперфосфата, опытное значение начальной скорости полного псевдоожижения которой а>о=0,76 м/с, da=0,89 мм и dQ= 1,89 мм, величина характеристики полнднсперсности я = 0,89/1,89= 0,47.

Характеристика полидиснерсиости, определяемая выражением (4.69), оценивает смесь частиц (гранул) по способности псевдоожиженного слоя да­вать определенный спектр выбросов в момент начала его псевдоожижения. Если при w=w0 выбросов нет илн онн незначительны, значит слой монодис - персный или очень мало от него отличается.

Статистический анализ структуры разреженной зоны неоднородного псев­доожиженного слоя с помощью максвелловского распределения частиц по начальным скоростям их вылета из плотной зоны слоя позволил углубить представления о некоторых физических связях, существующих между плотной и разреженной зонами слоя, твердыми частицами и ожижающим агентом.

Кроме того, рассмотренная статистическая модель образования разре женной зоны может быть использована для количественного описання про­цессов, граничным условием которых является распределение частиц по на­чальным скоростям в момент нх вылета в надслоевое пространство.

Перемешивание твердой фазы в псевдоожиженном слое. Ха­рактер движения частиц в псевдоожиженном слое определяет­ся двумя одновременно действующими факторами: крупномас­штабной циркуляцией пакетов через весь аппарат с некоторой скоростью и мелкомасштабными пульсациями, характеризуе­мыми эффективным коэффициентом диффузии D* [97]. В об­щем балансе перемешивания основная доля приходится на цир­куляцию через весь аппарат: коэффициент диффузии D* =

= (0,5—1,0) - ІО-4 м2/с на 1,5—2 порядка меньше общего коэф-

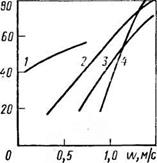
Рис. 4.13. Зависимость коэффициента турбу­лентного перемешивания D„eр от скорости w для стеклянных шариков диаметром 0,315 мм (/), 1,18 мм (3), 1,67 мм (4) и по - лидисиерсной смесн гранулированного су­перфосфата (2)

фициента D(30—40)-10-4 м2/с, оп­ределяющего степень перемешива­ния слоя в целом. Перемешива­ние за счет циркуляции пакетов происходит как в плотной фазе слоя при образовании и гидродина-

в надслоевом пространстве при выбросе и распаде пакетов.

Для количественной оценки еп можно использовать выражение (4.60). Полагая, что вероятность движения с той илн иной скоростью одинакова для пакета частиц в плотной фазе слоя и на поверхности слоя, можно рас­считать среднее время циркуляции пакета тц. п = Т//гД, где Н—масштаб дви­жения пакета (высота слоя).

Можно также определить порядок коэффициента турбулентного переме­шивания твердой фазы D„ep за счет движения пакетов [97]:

Оце j) - : 6,1 vnl. - (4.71)

Значения Опер, рассчитанные по уравнению (4.71), для всех исследован­ных систем находятся в диапазоне (20—80) ■ I0-4 м!/с (рис. 4.13). Увеличе­ние скорости ожижающего агента в области развитого неоднородного псев­доожиженного слоя приводит к интенсификации перемешивания твердой фа­зы. С уменьшением размеров частиц дисперсной системы влияние скорости потока на изменение D„ep уменьшается.

Определение времени прохождения частицей всего объема слоя под дей­ствием мелкомасштабных пульсаций является сложной задачей. Данные по так называемому эффективному коэффициенту диффузии получены на плос­кой модели идеализированного псевдоожиженного слоя, состоящего из одного ряда частиц [97].

Исследована [98] направленная циркуляция твердой фазы в конфузор- ном (сужающемся кверху) аппарате прямоугольного сечения размером 0.25Х Х0.06 м. Использовалась система сферических монодисперсных частиц алю­мосиликатного катализатора (rf.-, = 3,34 мм), содержащих некоторое количест­во меченых (пропитанных черной тушью) частиц того же размера. Скорости меченых частиц в различных зонах и время циркуляции определялись с по­мощью кинофотосъемки. Полное время циркуляции частицы Тц в слое с на­правленным движением твердой фазы складывается из времени ее опуска­ння в центральной части слоя в результате мелкомасштабных пульсаций Тц. ч и времени подъема при пакетном выбросе Тц. п в периферийной зоне, при­чем Тц. ч>Тц. п. _

Для среднего времени циркуляции Тц частиц получено следующее эмпи­рическое выражение:

Тц= 44 (///в)-б.» (/отв//)-0'6 (ta/tr0)-M. (4-72)

Формулой (4.72) можно воспользоваться для оценки порядка величины Тц. ч, применив ее к критическому состоянию слоя ш/юо=1 в аппарате посто­янного по высоте сечения (flfB= 1), когда появление пакетных выбросов ис­ключается. Тогда тц. ч= 150 с, а средняя скорость частиц при 77 = 0,2 м будет равна 0,0013 м/с.

В случае же развитого неоднородного псевдоожиженного слоя с актив­ным движением пакетов по всему его объему средняя скорость, определяе­мая по уравнению (4.60), находится в пределах 0,2—1,0 м/с. Из этого со­поставления видно, что средние скорости пульсаций одиночных частиц и их пакетов различаются более чем на 2 порядка и следовательно, на эту же величину должны отличаться друг от друга эффективный коэффициент диф­фузии D* И коэффициент турбулентного перемешивания твердой фазы Опер - Эти выводы находятся в соответствии с данными, полученными для диффу­зии частиц в двухмерном псевдоожиженном слое [97].

Таким образом, при наличии пакетных пульсаций в слое перемешивание твердой фазы определяется движением и взаимодействием пакетов частиц.

Степень перемешивания твердой фазы прн непрерывном процессе, как известно, оценивается отношением Тц/Т (где Т=Ссл/Сисх", Сел — вес слоя; Qисх — нагрузка по исходному продукту). Пренебрегая циркуляцией твердой фазы под действием мелкомасштабных пульсаций в неоднородном псевдо­ожиженном слое, условие нормирования распределения (4.58) можно запи­сать в виде:

ОО

<?ц = Тц/т(ЗиСХ= J / (1>п) <Hi. (4.73)

о

При Тц=Тц. ч, т. е. при вырождении крупномасштабных пульсаций, ха­рактерном в общем случае лишь для начала псевдоожижения слоя, отноше­ние Тц/х«) и для непрерывного процесса в таком случае будет характерен режим вытеснения.

В условиях развитого неоднородного псевдоожиженного слоя, когда Тц^т, будет происходить полное перемешивание частиц даже при очень зна­чительной нагрузке Qисх на аппарат.

4.2.4. Унос при гранулировании

Показано [99], что формирование уноса в грануляторе с псевдоожиженным слоем начинается на границе плотный слой — разреженная зона. В общем случае математическое опи­сание уноса сводится к совместному рассмотрению распреде­ления частиц по начальным скоростям их вылета из плотной фазы слоя и закономерностей движения частиц в надслоевом пространстве. При этом рассмотренное выше распределение час­тиц по начальным скоростям их вылета из слоя является гранич­ным условием задачи.

Закономерности движения частиц в надслоевом пространстве для раз­личных режимов обтекания их газовым потоком выражаются следующими

где g— ускорение свободного падения; z — высота подъема частицы. 106

В уравнениях (4.74) — (4.79) коэффициенты о, Ь, с постоянны для дан­ной псевдоожиженной системы и определяются следующим образом:

а=18р/Д2рт; fc=39v1/2pr/4ds/2pTg; с= l,44pr/4dpTg.

По зависимости вида 2 = ф(пч) и начальным скоростям вылета частиц в надслоевое пространство можно рассчитать максимальный путь их подъема. Аналитическое решение уравнений (4.74) — (4.79) даже для аппарата с про­стейшей геометрической конфигурацией надслоевого пространства (напри­мер, цилиндрической, т. е. когда n>(z) = const) затруднено. Значительно бо­лее приемлемым методом решения приведенных дифференциальных уравне­ний (4.74) — (4.79) является численный, осуществляемый с применением ЭВМ.

Зависимости вида z = <р(і'ч), найденные решением соответствующих урав­нений для аппаратов с различным законом изменения скороЛи ожижающе­го агента по высоте w=f(z), могут быть использованы для расчета необхо­димой высоты надслоевого пространства, определяющей минимальную вели­чину уноса материала, либо качество разделения исходной смеси (примени­тельно к классификаторам с псевдоожиженным слоем).

Расчет уноса. Расчет уноса в аппарате с неоднородным псев­доожиженным слоем при осуществлении в нем непрерывного установившегося процесса заключается в следующем.

Из распределения начальных скоростей вылета частиц для данного состояния псевдоожиженного слоя [см. (4.61)], прини­мая для системы с полным перемешиванием частиц в плотной фазе слоя условие нормирования:

оо

Qhcx = j* / (уч) du4 = I» (4.80)

0

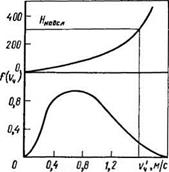
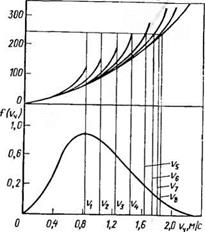
определяем долю частиц, попадающих в унос из монодисперсно - го псевдоожиженного слоя (рис. 4.14):

оо

Qy= J /Ы<К, (4.81)

v

где v4'— начальная скорость вылета частиц, соответствующая пути ее подъ­ема z, равному высоте надслоевого пространства Н„адел.

Частицы, вылетевшие из плотной фазы слоя с большей на­чальной скоростью, попадают в унос. Частицы, начальная ско­рость вылета которых меньше ш/, возвращаются в слой. На верхней половине графика рис. 4.14 изображена расчетная за­висимость г=ф(пч), полученная решением соответствующих дифференциальных уравнений движения частицы определенно­го размера для данного состояния псевдоожиженного слоя.

Величина уноса в аппарате с полидисперсным псевдоожи­женным слоем, очевидно, будет равна сумме количеств уноса каждой t-й фракции, т. е.

Qy=* У qyi - (4.82)

1=1

Величина уноса t'-й фракции qyi определяется подобно тому, как это было сделано для монодисперсного слоя, но с обяза-

тельным учетом содержания данной фракции в исходной смеси, загружаемой непрерывно в аппарат

счп

На верхней части графика (рис. 4.15) изображены расчет­ные зависимости вида z=f(v4) для каждой t-й фракции поли­дисперсного слоя.

Из ^выражения (4.85) нетрудно определить гранулометриче­ский состав уноса. Для оценки этого состава воспользуемся величиной относительной концентрации мелочи Y (частицы раз­мером менер граничного зерна drp) в уносе, т. е. Y—y/ (1-у), где у — содержание мелочи в уносе. Тогда из выражения (4.85) получим:

^чг ч3 ч4

it f f(v4)dvЧ+(І1-ЬІ2) j /Н*ч+ (І1 + І2 + Із) j / К)

Y =

45

(І1 + І2 + із + І4) j f (уч) 4уч + ■ - ■ + (Іі + І2 + • •• + in) J* f (ич)

rp

(4.86)

По уравнениям (4.85) и (4.86) можно также полностью рас­считать классификатор с псевдоожиженным слоем материала при необходимости разделения полидисперсной смеси на два продукта: верхний (унос) и нижний. Для этого в дополнение к указанным уравнениям следует рассмотреть уравнение балан­са материальных потоков, которые дают следующие величины верхнего Qy и нижнего Q„ продуктов в зависимости от содер­жания в них данного компонента, например мелочи, при задан­ном QHCX:

<?у=<?и«(£—*)/(» —*). (4-87)

<?и = Q«cx (y — t)l(y — X). (4.88)

Здесь х — содержание мелочи в нижнем продукте; Е; — со­держание мелочи в исходной смеси.

Таким образом, расчет разделения, заключающийся в опре­делении состава и выхода продуктов (верхнего и нижнего), сво­дится к решению уравнений (4.85) и (4.86) совместно с уравне­ниями баланса (4.87) и (4.88).

Расчет сепарационного пространства. В отличие от аппара­тов с неподвижным слоем материала сепарационное (надслое - вое) пространство грануляторов с псевдоожиженным слоем рассчитывают, исходя из соображений предотвращения или до­пустимости минимального уноса продукта. Как это следует из рассмотрения структуры однородного и неоднородного псевдо­ожиженных слоев, различают кинетический и динамический унос твердой фазы.

Для аппаратов с однородным псевдоожиженным слоем ха­рактерен только унос, связанный с превышением скорости ожи­жающего агента в сепарационном пространстве скорости вита­ния частиц данного размера. Такой вид уноса получил назва­ние кинетического.

В случае неоднородного псевдоожижения, сопровождающе­гося выбросом в надслоевое пространство пакетов твердых ча­стиц любого размера, в том числе и частиц, скорость витания

которых значительно больше скорости газа в сепарадионном пространстве, помимо кинетического имеет место унос, назы­ваемый динамическим. /

Основным условием предотвращения кинетического уноса является выполнение следующего неравенства: (

Шсеп^ї^вит (4.89)

(где Шсеп — скорость газа в сепарационном пространстве).

Изучение особенностей динамического уноса показало, что распределение начальных скоростей выброса пакетов частиц из псевдоожиженного слоя описывает в первом приближении и распределение начальных скоростей вылета отдельных частиц из плотной фазы слоя в надслоевое пространство.

■ Это предположение позволяет определить среднее и макси­мальное значения начальной скорости вылета частиц в надслое­вое пространство, исходя из анализа распределения выброса пакетов частиц из слоя.

Для монодисперсного слоя получено следующее выражение: сч= 0,09Ar°.25 Ig Шр/ш0. (4.90)

Для полидисперсного слоя (гранулированный суперфосфат) среднее значение скорости определяется как

йч = 0,5+ 1,3 lgo>„/ro0. (4.91)

Максимальное значение начальной скорости вылета частиц определяется с учетом дисперсии распределения по следующе­му приближенному уравнению:

^чтах^ЗСц' (4.92)

Сепарационное пространство грануляторов с псевдоожижен­ным слоем, как правило, рассчитывают с учетом обоих видов уноса. Диаметр сепарационной зоны определяют из расчета обеспечения скорости ожижающего агента меньше скорости витания самых мелких частиц (или частиц, унос которых допу­стим).

Высоту сепарационного пространства рассчитывают по урав­нению

Нееп>1^ч max/2g. (4.93)

Достоверность изложенной методики расчета подтверждена опытом эксплуатации промышленных грануляторов с псевдо­ожиженным слоем.