Гранулирование

Свойства материалов как объектов гранулирования

К наиболее важным свойствам материалов, определяющим эффективность процессов гранулирования и сопутствующих им процессов тепломассообмена, а в конечном итоге — качество готового продукта, относятся: смачиваемость порошков, их теплоемкость и теплопроводность, химический потенциал И СО­

противление пластическим деформациям, коэффициенты диф­фузии жидкости в них.

Смачивание. Смачивание характеризуют [24] как процесс, сопровождающийся образованием новых фазовых границ, и в зависимости от термодинамики процесса различают три типа смачивания:

1) контактное или адсорбционное смачивание;

2) смачивание погружением или пропиткой;

3) смачивание при растекании.

Основными энергетическими характеристиками поверхности твердых тел и жидкостей служат удельная свободная поверх­ностная энергия ДЭ и поверхностное натяжение о, вследствие чего процессы смачивания удобно описывать (для случаев 1—3) термодинамически следующим образом [24]:

ДЗі — Ст. ж— (Сж, г4“Ст, г)» (1*1)

Д3г= От. ж—1 Ож. Г) (1*2)

ДЭз= (Ст. жЧ-Сж. г) СТт. г, (1.3)

где от, ж, Ож, г, От, г — поверхностные натяжения на границе контакта фаз; индексы т, ж, г — твердая, жидкая н газовая фазы.

Во многих случаях должно выполняться условие: ДЭ<0. В то же время для равновесного состояния твердой, жидкой и газовой фаз справедливо следующее соотношение (уравнение Дюпре):

От, г= От, ж-(-Ож, г COS 0, (1*4)

где G—краевой угол смачивания, отсчитываемый от поверхности жидкой фазы.

То же уравнение, но записанное относительно cos60, назы­вают [25] уравнением Юнга:

COS 00= (oTlr— От, ж)/Ож, г - (1.5)

Поскольку значения от, г и от, ж экспериментально определить не удается [24], авторы [25], используя понятие работы адге­зии, уравнение (1.5) преобразуют к следующему виду:

COS 00= (Аа — Ож, г)/Ож, г» (1.6)

где /1а—работа адгезии, характеризующая взаимодействие двух конденсиро­ванных фаз в расчете на единицу площади контакта.

Для расчета работы адгезии используют различные теоре­тические методы [26, 27], в том числе на основе молекулярной теории смачивания, например для систем с преобладающей до­лей дисперсионных взаимодействий между жидкостью и твер­дым телом [28]. Так, при рассмотрении краевых углов смачи­вания порошков предполагают [28], что взаимодействие меж­ду молекулами двух фаз, находящихся в контакте, определя­ется силами нескольких типов. Они могут быть представлены суммой работ адгезии для различных видов взаимодействий,

Член Лат’ж'г,<г — учитывающий вклад дисперсионных сил, обычно является доминирующим. Итак, из уравнений (1.6) и (1.7) следует, что образование острых краевых углов возмож­но лишь при условии:

(1.8)

при Ла<Сж, т смачивание отсутствует.

Из вышеизложенного можно сделать вывод, что измерение величины краевых углов смачивания дает наглядный способ проникновения в природу и характер сил, существующих на границе раздела фаз, а'значит и возможность влиять на про­цесс формирования гранул.

В производстве минеральных удобрений в качестве твердой фазы используется порошкообразный материал, поэтому опре­деление краевого угла пористых тел представляет особый прак­тический интерес.

Литературные сведения об определении краевых углов сма­чивания порошкообразных материалов весьма ограничены и противоречивы [24, 25, 29].

Наиболее простой способ [29] основан на измерении скоро­сти подъема жидкости по капиллярам порошка:

/і2ж — ТЖГпО COS 0/2(1 л:,

где кж — высота подъема жидкости в порошке; тж — время подъема жидко­сти; гп—эквивалентный радиус пор; о — поверхностное натяжение жидко­сти; 0—краевой угол смачивания; рж—вязкость жидкости.

Однако сложности, связанные с определением эквивалент­ного радиуса пор реальной засыпки порошка, делают это урав­нение недостаточно пригодным для расчета краевого угла 6. В результате определение высоты Аж смачивающей жидкости становится весьма затруднительным.

Предложен [30] метод расчета краевого угла, позволяющий избежать трудностей, связанных с определением гп. В этом случае вместо длины пути, пройденного жидкостью в порошке, определяют скорость ее впитывания. Чтобы исключить влияние неоднородностей пористого образца, автор [30] предложил проводить дополнительные опыты по определению скорости впитывания исследуемым порошком неполярных жидкостей (бензол, тетрахлорид углерода и т. п.) с малым поверхностным натяжением, для которых установлено, что cos0=1, т. е. 0 = = 0°. Тогда уравнение (1.9) после ряда преобразований прини­мает следующий вид:

где ив, ев—скорости впитывания воды и бензола соответственно; рв, pie — вязкости воды и бензола; а,, ав — поверхностное натяжение воды и бензола.

Этот метод [30] был впервые применен [31] для определе­ния краевых углов порошкообразных минеральных удобрений со следующей корректировкой: в качестве жидкой фазы вместо дистиллированной воды использовали насыщенные растворы исследуемых удобрений с тем, чтобы предотвратить их раство­рение. Описанная установка [31] позволяет автоматически фиксировать массу жидкости, впитываемой исследуемым мате­риалом в единицу времени. Представлены [31] результаты оп­ределения краевых углов смачивания для некоторых видов по­рошкообразных минеральных удобрений.

Особое значение оценка смачиваемости приобретает при ор­ганизации технологии гранулированного хлорида калия, кото­рая предусматривает введение на определенных стадиях алифа­тических аминов с числом углеродных атомов от 7 до 20. Та­ким образом, в готовом продукте присутствуют примеси али­фатических аминов, которые гиидрофобизируют поверхность и могут препятствовать смачиванию порошкообразного хлорида калия, а значит, и его способности к гранулообразованию сов­местно с другими компонентами.

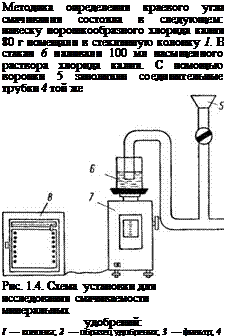
С целью изучения влияния алифатических аминов на сма­чивание хлорида калия, а следовательно, на процесс грануло - образования, в лабораторных условиях проведены исследова­ния на различных марках этого продукта. Определение краево­го угла смачивания проводили по известной методике [31] на усовершенствованной установке, представленной на рис. 1.4.

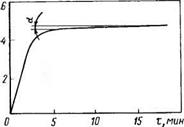Рис. 1.5. Кинетика поглощения жидкости образцом—зависимость Сж=/(т)

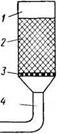
Рис. 1.6. Схема установки для исследования кинетики поглощения жидкости:

1 — исследуемый образец; 2 — стакан с водой; 3 — весы ВЛТК-500; 4 — устройство для

подвески образца

жидкостью и перемещали колонку 1 так, чтобы жидкость прошла через фильтр 3 и начала смачивать исследуемый порошок 2. С целью исключения влияния избыточного давления воздуха, создаваемого при заполнении соеди­нительных трубок жидкостью, внутри колонки 1 установлен капилляр, кото­рый позволяет значительно увеличить точность измерения.

Количество впитанной жидкости замеряли на весах 7, которые имели ин­дукционный датчик, позволяющий фиксировать изменение массы жидкости С в стакане 6 во времени т иа диаграммной ленте потенциометра 8. Скорость впитывания определяли как тангенс наклона а кривой G—f(x) к оси т (рис. 1.5).

Полученные экспериментальные данные использовали для расчета крае­вого угла смачивания по уравнению [31]:

cos 0 = ЦрЦр Оу/ЦуЦуОр,

где о, р, а — соответственно скорость впитывания, вязкость и поверхностное натяжение раствора хлорида калия (индекс р) и тетрахлорида углерода (ин­декс у).

Значения вязкости и поверхностного натяжения тетрахло­рида углерода заимствованы из работы [31]. Исследования про­ведены на следующих образцах хлорида калия: химически чис­том, галургическом, содержащем в своем составе амины (330 г/т), и флотационном (140 г/т).

Расчетные значения краевых углов смачивания, приведен­ные ниже, получены при использовании в качестве смачиваю­щей жидкости насыщенных растворов указанных марок хлори­да калия со следующими показателями свойств:

и галургический хлорид калия не смачиваются насыщенным раствором. Это объясняется гидрофобизирующим действием алифатических аминов, содержащихся на поверхности его кри­сталлов.

Добавление азотной кислоты к насыщенному раствору КО (любых марок) приводит к уменьшению краевого угла, т. е. к улучшению смачивания хлорида калия:

На основании проведенных исследований можно сделать важный в практическом отношении вывод: с целью интенсифи­кации процесса гранулирования сложных удобрений, одним из основных компонентов которых является хлорид калия, целе­сообразно перед гранулированием или в процессе гранулирова­ния обрабатывать удобрение кислыми растворами.

Диффузия влаги. Методы определения коэффициента диф­фузии основаны главным образом на закономерностях стацио­нарного массообмена [32]. Все они осложняются большой дли­тельностью проведения эксперимента. Кроме того, существую­щие приборы или ограничивают область влагосодержания, да­вая возможность определять этот коэффициент только в гигро­скопической области, или не позволяют избежать погрешностей, обусловленных краевыми эффектами.

Ввиду этих недостатков авторы [32] предложили методику определения коэффициента диффузии влаги с использованием данных по кинетике увлажнения пористых материалов. Теоре­тическое обоснование разработанной методики базируется на решении уравнения изотермического переноса влаги в капил­лярно-пористых материалах:

ди(х, х)/дх = атд2и/дх2 (т>0, — гш<х<гш), (1.11)

где и — текущее значение влагосодержания материала; х — текущее значе­ние радиуса шара; т — время; а„, — коэффициент диффузии влаги; гш—ра­диус шара.

Решая уравнение (1.11) при начальных и граничных усло­виях первого рода

U(X, 0)=0, U (/Ти, т) = Мщах, К(—г, г, г)

(где Птах —максимальное влагосодержание материала), авто­ры [32] получили расчетную формулу для определения коэффи­циента диффузии:

Ят= tg а (ггш/ц2п ), (1.12)

где tg а=(1п В (Ті)—1п В (Тг)]/(т2—о); ть т2 — два дискретных значения вре­мени^ В (т) = 1—[її (Т) | г/max), где и — среднее влагосодержание материала.

В случае шара ап=п, для цилиндра — является корнем функции Бесселя: р„=2,4048 [32].

Далее авторы отмечают, что экспериментально осуществить процесс, удовлетворяющий описанной задаче, довольно просто. Для этого необходимо абсолютно сухой образец погрузить в дистиллированную воду и снять кривую кинетики увлажнения образца. При этом необходимо, чтобы образец и вода находи­лись при одинаковой температуре.

Схема экспериментальной установки [32] представлена на рис. 1.6. В ста­кан с водой погружают подвешенный с помощью устройства 4 к весам 3 марки ВЛТК-500 образец 2. При увеличении влагосодержаиии образца 2 вес его увеличивается. Показания весов записывают через определенные промежутки времени вплоть до постоянного веса, когда образец перестает впитывать влагу. По этим данным строят кривые кинетики увлажнения об­разца, а после их обработки рассчитывают коэффициенты диффузии влаги в различных строительных материалах.

Эта методика обладает одним недостатком — при снятии кривых кинетики увлажнения образца авторы [32] не учиты­вали количество испарившейся за время эксперимента жидко­сти. Эта методика была принята для определения коэффици­ентов диффузии влаги в концентрированных и сложных удоб­рениях с учетом испарения влаги.

После снятия кривых кинетики увлажнения определяли ко­эффициент tga, а по уравнению (1.12) рассчитывали коэффи­циент диффузии влаги. Известно, что в промышленных усло­виях при осуществлении процессов гранулирования в аппарат возвращают ретур при 40—87 °С, на который распыливается жидкая фаза при 40—115 °С (в зависимости от схемы произ­водства). С учетом этого, в лабораторных условиях проведены исследования зависимости коэффициентов диффузии влаги от температуры. Кривые кинетики поглощения влаги снимали при изотермических условиях путем термостатирования установки. Относительная погрешность определения коэффициентов диф­фузии влаги не превышала 5%.

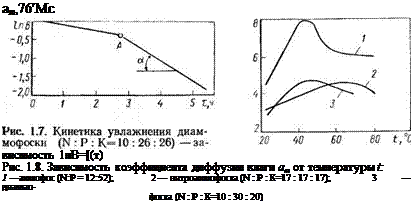На рис. 1.7 в качестве примера представлена типичная кри-

вая кинетики увлажнения диаммофоски марки 10:26:26, по­строенная в полулогарифмических координатах. Из рисунка видно, что интенсивное поглощение жидкости образцом наблю­дается после насыщения поверхностного слоя (точка А). Как указывалось выше, используя прямолинейную зависимость 1пБ=/(т), вычисляли tg а угла наклона этой прямой к оси абс­цисс, а затем по формуле (1.12) рассчитывали коэффициенты диффузии влаги ат, 10~9 м2/с в концентрированных и сложных удобрениях для температуры 22 °С (табл. 1.2).

Сопоставление данных по коэффициентам диффузии и по­ристой структуре изучаемых образцов представлено в табл. 1.2. Пористость образцов определяли методом вдавливания ртути в поры удобрений на установке ПР-3.

Из табл. 1.2 видно, что при близких значениях пористости, коэффициент диффузии влаги ат в ряду удобрений аммофос — диаммофоска 10:30:20 имеет тенденцию к уменьшению. При этом, несмотря на довольно высокое содержание крупных пор с радиусом Гп>10~7 м для нитроаммофоски 17:17:17 — 75,8% и диаммофоски 10:30:30 — 53,3%, коэффициенты диффузии ат имеют самые низкие значения—3,2-10-9 м2/с и 2,9-10~9 м2/с соответственно, что объясняется, по-видимому, наличием в их составе хлорида калия, гидрофобная поверхность которого за­медляет продвижение жидкости по капиллярам образца.

Полученные результаты по кинетике влагопоглощения и рассчитанные коэффициенты диффузии исследуемых удобрений характеризуют влагопроницаемостъ твердой фазы при / = 22 °С. В промышленных условиях, как указывалось выше, при осу­ществлении процессов гранулирования поддерживается темпе­ратура до 100 °С в зависимости от технологических параметров процесса. Температурная зависимость am=f(t) для некоторых видов минеральных удобрений (рис. 1.8) показывает, что коэф­фициент диффузии с увеличением температуры возрастает до выраженного максимума при /~50°С, равного для аммофоса

am=8,0-10"9 м2/с, для диаммофоски 10:30:20 — am=4,7x ХЮ~9 м2/с, а затем уменьшается до некоторого постоянного зна­чения. Для нитроаммофоски максимум выражен нечетко и смещен в сторону больших температур.

Экстремальный характер зависимости am = f(t) можно объ­яснить следующим образом. В области температур 20—40 °С перенос диффундируемого вещества в объем гранулы происхо­дит, в основном, в процессе его стока по поверхности пор. При этом с увеличением температуры вязкость диффундирующего вещества уменьшается, что приводит к увеличению эффектив­ного коэффициента диффузии.

В области температур более 40 °С в результате расширения газовой фазы перенос диффундирующего вещества протекает в объеме пор через газовую фазу, что приводит к снижению эффективного коэффициента диффузии.

В области температур 20 °С — tK. p (где /И. Р — температура начала разложения образца), т. е. в рабочем диапазоне, зави­симость коэффициента диффузии влаги от температуры прини­мает вид:

em=am0exp(fe/)-

После обработки экспериментальных данных для удобрений получено значение постоянного коэффициента k при темпера­туре разложения менее 60 °С К=0,02, при ^>60 °С К=0,025.

Теплофизические и термодинамические свойства удобрений. Известно, что к основным теплофизическим показателям мате­риала относится коэффициент температуропроводности. Для его расчета необходимо знание коэффициентов теплопроводности, теплоемкости и плотности [33]. Эти параметры определены для удобрений: аммофоса, полученного на основе кислоты из апа­тита диаммонийфосфата 18:48, нитроаммофоски 13:19:19, нитродиаммофоски 17:17:17, диаммофоски 10:26:26. Иссле­дования проведены в диапазоне температур 25—80°С, который соответствует возможному изменению температуры материала в процессе гранулирования и сушки.

Теплопроводность исследуемых образцов определяли на приборе ИТ-3, в основу работы которого заложен стацио­нарный метод пластины [34], основанный на измерении тепло­вого потока, пронизывающего образец испытуемого материала, имеющего форму пластины.

Исследование зависимости теплоемкости сложных удобрений от температуры проводили калориметрическим ме­тодом [34]. Сущность метода заключается в том, что исследуе­мый образец, запаянный в платиновую ампулу, нагревают в вертикальной трубчатой электропечи, а затем помещают в ка­лориметр, находящийся в водяном термостате при 25 °С. По ве: личине подъема температуры калориметра определяют опыт­ное значение энтальпии. Калибровку калориметрической уста­новки осуществляли измерением в ней энтальпии синтетическо-

го сапфира а-АЬОз — вещества, рекомендуемого для этой цели. Точность измерения энтальпии в интервале температур 25— 80 °С составляла ± 1,5%.

Значения теплопроводности представлены в табл. 1.3. Там же приведены экспериментальные значения насыпной и пикно­метрической плотности сложных удобрений различных марок.

Используя данные по теплопроводности, теплоемкости и плотности, рассчитывали коэффициенты температуропроводно­сти, значения которых представлены в той же таблице. Анализ представленных данных показывает, что теплоемкость, тепло­проводность, а следовательно, и коэффициент температуропро­водности в исследованном диапазоне температур практически в пределах точности измерений не изменяются.

Определение химических потенциалов. Химический потен­циал характеризуется приращением внутренней энергии данно­го компонента системы на единицу, если давление, температура и масса всех остальных компонентов системы остаются по­стоянными.

Проведены исследования [35] зависимости химического по­тенциала и коэффициента термовлагопроводности от влагосо - держания для ряда минеральных удобрений, выпускаемых оте­чественной промышленностью. Учитывая, что в настоящее вре­мя ряд заводов отрасли переходит на выпуск новых видов слож­ных удобрений (диаммонийфосфата, диаммофосок) в лабора­торных условиях проведен комплекс исследований по опреде­лению энергии связи и коэффициентов термовлагопроводности для новых марок удобрений.

Методика определения указанных выше термодинамических параметров заимствована из работы [35]. Сущность методики заключается в снятии изотерм сорбции исследуемых образцов минеральных удобрений. Затем рассчитывают энергию связи влаги с материалом (ц = 7?і/1пф) для разных относительных влажностей ф воздуха и температуры. На основании графиков li = f(u, t) рассчитывают изотермическую удельную массоем - кость по соотношению с'т — (du/dn)t и методом графического дифференцирования определяют температурный коэффициент

химического потенциала (dijdt)u, а затем рассчитывают коэф­фициент термовлагопроводности из выражения:

b=c'm (dp./dt)u.

Исследование процесса сорбции паров воды образцами ди - аммофосок марок 10:26:26 и 10:30:20, полученными из хи­мически чистых солей, проводили импульсным хроматографиче­ским методом.

Исследуемый образец помещали в термостатированную колонку газово­го хроматографа «Цвет-102», прогревали в потоке гелия при 55 °С до уда­ления гигроскопической воды. Затем при 20 °С микрошприцем вводили дозу воды.

Варьированием условий контакта твердой и газовой фаз было установ­лено, что для исследуемых солей возможно получение хроматограммы, фор­ма которой обусловлена преимущественно равновесными факторами и не зависит от условии эксперимента: расхода газа-носителя в пределах (1,8— 4,8) -10-3 м3/с, величины навески (1—10)-10-3 кг, дисперсности соли (0,05—-0,10) -10—3 м, величины вводимой дозы воды (0,1—20)-Ю-6 кг.

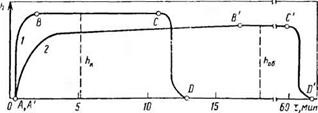
На такой равновесной хроматограмме (рис. 1.9) можно выделить три участка: участок АВ, соответствующий размыванию переднего края зоны, характеризует начальную стадию процесса; примолинейный участок ВС, со­ответствующий постоянному давлению пара над солью; участок CD, соот­ветствующий размыванию правой части хроматограммы, который практиче­ски совпадает с участком кривой холостого опыта.

Размыванию переднего края хроматограммы ЛВ соответствует изотер­ма, обращенная выпуклостью к оси давления пара.

Для получения абсолютных значений давлений пара Лоб применяли сле­дующий способ калибровки: достаточно большую дозу воды вводили в ко­лонку с инертным материалом (плавленой кварцевой крупой), регистрируя при этом ступенчатую хроматограмму, высота которой (Лк) соответствует табличной величине давления насыщенного пара воды при данной темпера­туре. Относительная погрешность этого метода калибровки составляет ±2% (отн.).

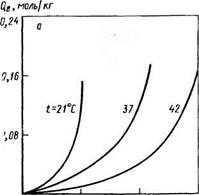
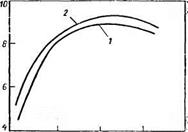
Изотермы сорбции паров воды в диапазоне температур 26—45 °С показывают, что сорбционная емкость диаммофоски марки 10:26:26 (рис. 1.10, а) существенно больше, чем марки 10:30:20 (рис. 1.10,6). Например, при температуре 12 °С, количество сорбированной влаги QB на диаммофоске марки 10:26:26 составляет 0,08 моль/кг, а марки 10:30:20 — 0,07 моль/кг. Это объясняется тем, что диаммофоска марки 10:26:26 имеет значительно большую удельную поверхность, чем марки 10:30: 20.

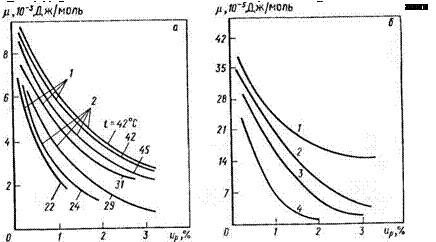
На рис. 1.11, а представлены зависимости химического по­тенциала для исследованных образцов от влагосодержания, а на рис. 1.11,6 для сравнения представлены эти же зависимо­сти для других минеральных удобрений, заимствованные из работы [35].

На рис. 1.12 представлены зависимости коэффициента тер - мовлагопроводности от влагосодержания: с увеличением влаго­содержания коэффициент термовлагопроводности сначала уве­личивается, а затем уменьшается. Это уменьшение вызвано тем, что, как указывается в работе [35], с повышением влагосодер­жания количество адсорбционно связанной влаги по сравне­нию с осмотически связанной влагой постепенно уменьшается. Максимум на кривой характеризует момент, когда тепло ад­сорбции нс выделяется и начинается период капиллярной кон­денсации.

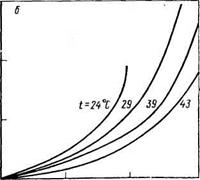0 / 2 Р„,кПа о I 2 Р„, кПа

Рис. 1.10. Изотермы сорбции паров воды на диаммофоске:
а — N : Р : К=10 : 26 : 26; 6 — N : Р ; К=10 : 30 : 20

Адгезионные свойства. В процессе транспортирования, при погрузочно-разгрузочных работах минеральные удобрения под­вергаются воздействию статических (гравитационных) и ди­намических (вибрационных) нагрузок. При этом наблюдается налипание материалов на различные поверхности, обусловлен­ное действием адгезионных сил. Кроме того, известно, что в процессе прессования порошкообразных материалов, особенно минеральных удобрении, происходит их налипание на валки.

В общем случае интенсивность этого процесса можно оце­нить либо силой прилипания, либо числом адгезии, которое по­казывает отношение числа частиц, оставшихся на подкладке, к начальному числу частиц на ней при данной силе отрыва [36]. Известны и другие методы исследования адгезии частиц порошка к различным поверхностям. Однако ни один из пред­ложенных методов не может быть использован для оценки к~'

адгезионных свойств порошко­образных удобрений в процес­се их непрерывного уплотне­ния на валковых прессах.

Рис. 1.12. Зависимость коэффици­ента термовлагопроводиости 6 ди­аммофоски марок 10 : 26 : 26 (/) и 10 : 30 : 20 (2) от влагосодержа­ния ир

Вполне очевидно, что величина адгезионных сил зависит от параметров процесса прессования: давления на валки, влажно­сти прессуемого материала и его гранулометрического состава. Измерение адгезионных сил в условиях непрерывного формо­вания практически невозможно. С целью максимального при­ближения к реальному процессу уплотнения разработаны ме­тодика и прибор для проведения исследований адгезионных свойств порошкообразных материалов [37].

Методика сводится к предварительному уплотнению материала и по­следующему измерению усилий отрыва плоской поверхности от исследуемого материала при помощи прибора, сконструированного на основе аналитиче­ских весов типа АВД-200. Одну из подвесных чаш весов заменили жестким стержнем, на нижнем конце которого закреплен пуансон пресс-формы. Для равномерного отрыва пуансона по всей плоскости соприкосновении с мате­риалом пресс-форму устанавливали иа подставке при помощи уровня. Адге­зионные силы А рассчитывали по уравнению

A=F0!Su

где F0 — усилие отрыва пуансона от материала, Н; Si — поверхность отры­ва, м2.

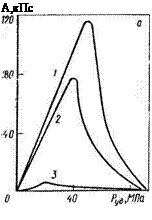
На рис. 1.13, а приведены зависимости адгезионных сил раз­личных минеральных удобрений от давления уплотнения Руд. Кривые имеют экстремальный характер, причем адгезионные силы принимают максимальные значения в области малых дав­лений. Указанные явления объясняются следующим образом. По мере увеличения давления прессования до определенного предела происходит уплотнение прессуемого материала с соот­ветствующим увеличением площади контакта частиц материа­ла с поверхностью пуансона, вследствие чего возрастают адге­зионные силы. При превышении этого предела адгезионные

Рнс. 1.13. Зависимость адгезионных сил А от различных условий:

•и — от давления уплотнения Руд: / — аммофос из апатита (№=1.05%); 2 — трнполифое-
фат калия (№=0,1%); 3 — РК-смесь № 1 (№=2.2%);

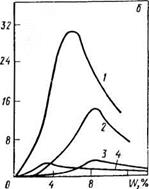
«6 — от влажности удобрений: / — аммофос нз апатита; 2 — аммофос из фосфоритов Ка-
ратау; 3 — РК-смесь № 1; 4 — хлорид калия

силы уменьшаются вследствие образования тонкой пленки воды, выдавливаемой из прессуемого материала.

На рис. 1.13,6 представлены зависимости адгезионных сил минеральных удобрений от влажности. Исследования проводи­ли при постоянном давлении, равном 263 МПа, что соответству­ет давлению прессования в промышленном прессе [38]. При влажности удобрений, близкой к нулю, адгезионные силы опре­деляются величиной поверхностной энергии контактных участ­ков. При возрастании влажности до определенного предела увеличение адгезионных сил связано, по-видимому, с ростом эф­фективной площади контакта за счет дополнительных жидкост­ных контактов, образующихся в местах выпрессовывания вла­ги. При дальнейшем увеличении влажности наблюдается уве­личение толщины пленки жидкости, и адгезионный контакт поверхность — материал заменяется контактом жидкость — жидкость. В этом случае наблюдается когезионный разрыв внутри пленки жидкости и, как следствие, уменьшение адгези­онных сил. В опытах с фосфорно-калийной смесью при влажно­сти 10,9% поверхности исследуемого образца и пуансона после отрыва были покрыты пленкой воды, хорошо различаемой не­вооруженным глазом. Из рисунка видно, что наиболее адгези­онно активным удобрением является аммофос, полученный на основе кислоты из апатита.

Результаты исследования адгезионных свойств удобрений дают возможность обосновать увеличение эффективности прес­сования на валковом прессе при установке в его бункере под - прессователя, а также выбрать развиваемое им оптимальное давление. При работе подпрессователя развивается небольшое давление в слое материала и на поверхности контакта валок — прессуемый материал. За счет этого увеличивается адгезион­ное сцепление между поверхностью валка и частицами мате­риала. Следовательно, интенсифицируется захват материала валками, и в результате увеличивается плотность прессованного материала.

На основании проведенных исследований рекомендуются следующие оптимальные давления подпрессовки: для фосфор­но-калийных удобрений 25—30 МПа, для хлорида калия 35— 40 МПа. Кроме того, полученные экспериментальные данные могут быть использованы для оценки налипания материала на стенки аппарата при расчете грануляторов барабанного типа, а также устройств, в которых удобрения подвержены действию статических (гравитационных) и динамических (вибрацион­ных) нагрузок. К таким устройствам относятся бункеры, ваго­ны, транспортеры. Данные по адгезионным свойствам мине­ральных удобрений представляют также практический интерес для конструкторов, занимающихся расчетом и разработкой очистных устройств валковых прессов и грануляторов бара­банного типа.

Сопротивление дефорациям. По представлениям, развитым

Зі

П. А. Ребиндером, важнейшие физико-механические свойства физических тел — прочность, пластичность, вязкость — обуслов­ливают способность их сопротивляться деформациям и разру­шению под действием внешних сил, т. е. исследуя указанные выше свойства материала, можно прогнозировать величину давления, необходимого для получения продукта заданной плотности.

Для оптимизации процесса уплотнения порошкообразных удобрений определенный интерес представляет оценка физико­механических свойств исходного сырья путем определения ка­кого-либо параметра, характеризующего влияние этих свойств на процесс уплотнения. Таким параметром, синтезирующим влияние физико-механических свойств порошкообразных мате­риалов, является их пластическая прочность.

Предложен метод определения пластической прочности ма­териалов по картине развития деформации при постоянной нагрузке, действующей на конус пластомера и возрастающей от опыта к опыту. Такой способ определения пластической проч­ности мелкодисперсных керамических масс дает возможность осуществить их структурно-механическую классификацию. Од­нако этот метод не позволяет определить условия уплотнения порошкообразных удобрений.

Решение данной задачи возможно на основании результа­тов исследования реологических свойств порошкообразных удобрений, которые до настоящего времени другими авторами не проводились.

В общем случае, как при прессовании материала, так и при погружении конуса на определенную глубину совершается ра­бота образования контактной поверхности:

л

AK=Pdh, (1-13)

6

где Р — сила, действующая на конус (или пуансон), Н; h — глубина погру­жения конуса или пуансона в исследуемый материал, м.

Проинтегрировав уравнение (1.13) для различных условий образования контактной поверхности, можно получить соотно­шение между давлением прессования и пластической проч­ностью порошкообразных материалов.

Для определения работы образования контактной поверх­ности Ак по глубине погружения конуса предложено уравнение

л

Ак — | Р d/i = окя03коН/24 tg а/2,

О

где 0к — напряжение в материале в местах контакта с конусом, Па; DKOh — диаметр конуса, м; а —угол при вершине конуса.

При прессовании порошкообразных материалов в пресс-мат­рице работа образования контактной поверхности А'к опреде-

ляется уравнением

где Г — площадь сечения пуансона, м2; Н„ — высота первоначальной засып­ки материала в матрице, м; hK — конечная высота спрессованного материа­ла. м; Руд — давление уплотнения, Па.

Из условия постоянства массы порошка до п после уплот­нения следует:

Ни — (Рл/рн)/ік — Z/lK.

Тогда

А'и—РsaF(z—

Очевидно, что при погружении конуса в исследуемую систе­му для достижения плотности материала в конкретной зоне, эквивалентной его плотности в случае прессования в матрице, требуется совершить значительно большую работу.

На основании изложенного:

AJA'K= Ок(я£>Л24 tgа/2) [РудР(г - 1)/ь]

ИЛИ

Рул~ KiKzOk", Руд—KOki

где Кі=АнІА'к—коэффициент, характеризующий соотношение работ при по­гружении конуса и пуансона; K2=nDKs/[24 tga/2F(2—1)/гк] — коэффициент, характеризующий соотношение контактных поверхностей при погружении ко­нуса и пуансона.

Глава 2