Пропускная способность барабанного аммонизатора
При вращении барабана материал в нем перемещается вдоль (по оси вращения) и поперек (перпендикулярно ей). Поперек вращающегося барабана материал перемещается под действием •сил тяжести, трения и центробежной. После достижения вместе •с обечайкой предельного угла рд нарушается равновесие тела относительно поверхности барабана, сдвигающая сила становится больше силы трения и тело начинает перемещаться вниз. Движение материала вдоль оси барабана обусловлено разностью давлений на входе в цилиндрическую обечайку и выходе из нее. Перепад давлений создается при понижении уровня материала, вызванном его обрушением на разгрузочном конце. Заполнение барабана зависит от свойств материала и параметров его движения.
Зная заполнение на конце барабана, его пропускную способность определяют из следующих соображений. Количество скатывающегося в гладкостенном вращающемся барабане материала (из условия неразрывности потока) равно количеству поднимающегося материала, тогда
Тп/Тск~ Сск5п/Сп5ск ~ F ск,
тде тп, Тек — продолжительность подъема и скатывания частиц; ц„, и<.к — скорости подъема и скатывания частиц; s„, scк — пути подъема и скатывания частиц; Fл, Fck — площади поперечного сечения поднимающегося и скатывающегося материала.
|
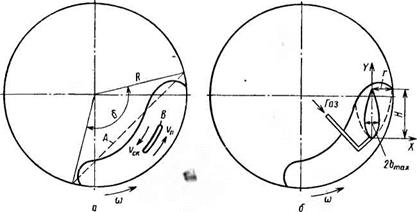
Рис. 6.1. Схемы движения материала (о) и газа (б) в поперечном сечении вращающегося барабана (Л — профиль слоя в неподвижном барабане; В — нейтральная область) |
Обозначив Fn/F06=ty (где Fав — площадь поперечного сечения материала в барабане), принимаем, что максимальный путь скатывания равен хорде, проведенной между крайними точками - засыпки. Как следует из рис. 6.1,
vcJv„- [ф/(1 — ф)12/? sin (6/2)//?в=2чр sin (6/2)/(1 — ф)6, где 6 — угол охвата засыпки в неподвижном барабане.
Скорость подъема материала определяется параметрами вращения барабана и в среднем равна vn=(oRI2.
Средняя скорость скатывания в поперечном сечении
sin (6/2)/(1 — ф)6. (6.1)
Из этой формулы, задаваясь оптимальной скоростью скатывания и коэффициентом заполнения, определяют частоту вращения барабана.
При подаче материала во вращающийся барабан происходит повышение его уровня в загрузочной части. Наклонная поверхность образуется не только в поперечном, но и в продольном сечении, за счет чего и происходит его перемещение вдоль оси. На разгрузочном конце материал расположен в поперечном сечении под углом естественного откоса в движении рд, а в продольном сечении — под углом Рд—а (где а — угол наклона барабана). Скорости скатывания в продольном и поперечном направлениях пропорциональны пути скатывания. Из геометрических соотношений:
сСкпр0дКк = [1 —cos (6/2)]/2 sin (Рд a) sin (6/2). (6.2)
Скорость перемещения вдоль оси барабана:
г>ос = ^скпродсо5 (Рд-а), (6.3)
1/ос = Дшф[1 — cos (6/2) 1/26(1 — if)tg(P* —а). (6.4)
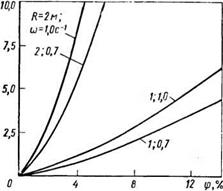
Рис. 6.2. Зависимость пропускной способности гладкостенного вращающегося барабана Q от его заполнения ф для различных радиусов R и частот вращения to барабана
 Пропускная способность вращающегося барабана определяется осевой скоростью и сечением материала, обрушивающегося на разгрузочном конце:
Пропускная способность вращающегося барабана определяется осевой скоростью и сечением материала, обрушивающегося на разгрузочном конце:
Q = tf3toi|j[l — cos(6/2)] (6 —sin6)/ /46(1 — $)tg(PA — a). (6.5)
Зависимости Q от ф для барабанов различного диаметра при различной скорости их вращения приведены на рис. 6.2.
Вывод уравнения (6.5) построен на зависимости производительности барабана от его заполнения на разгрузочном конце и не учитывает заполнения в рабочей зоне. Одним из важных условий проведения процессов гранулирования, аммонизации и других является поддержание оптимальной высоты слоя именно здесь. Анализ формулы (6.5) показывает, что требуемое заполнение достигается только при определенном соотношении расхода материала, скорости вращения и угла наклона барабана. Для выявления конкретной зависимости применительно к продуктам узкого гранулометрического состава (1—5 мм) проведены экспериментальные исследования.
С увеличением скорости вращения барабана увеличивается скорость осевого перемещения материала и при постоянной удельной производительности Q уменьшается коэффициент заполнения (рис. 6.3,с). С удельной нагрузкой, начиная с 0,5 т/(м2-ч), как и с углом наклона барабана высота слоя связана линейно (рис. 6.3,6). В результате обработки экспериментальных данных получена зависимость (v в м/с):
H/D = 0,02 - f- 0,I8Qtr-°.№ (0,112 —tgct), (6.6)
справедливая для @=0,5—10,0 т/(м2-ч).
Максимальное отклонение экспериментальных данных от рассчитанных по уравнению (6.6) для барабанов диаметром до 4,5 м и пропускной способностью до 300 т/ч составляет ±20%.
Высота слоя, рассчитанная по уравнению (6.6), является минимальной в необрушившемся слое. По мере удаления от зоны выгрузки высота слоя возрастает, причем слой имеет выпуклый профиль. Зависимость коэффициента заполнения барабана от его относительной длины приведена иа рис. 6.3, в, из которого видно, что интенсивность роста слоя зависит от удельной производительности аппарата.
Создание требуемой высоты слоя возможно путем установки подпорного кольца. Экспериментально показано, что при отсутствии подачи материала уровень слоя после остановки барабана близок к горизонтали, и зона действия кольца зависит от его высоты и угла наклона барабана. Высота слоя над подпорным кольцом возрастает с увеличением производительности,
а его профиль на длине (4-ь5)D эквидистантен профилю слоя в барабане без подпорного кольца. Следовательно, полученная зависимость пригодна и для барабанов с подпорным кольцом.