Гранулирование

Истечение газа во вращающийся слой зернистого материала

Взаимодействие движущихся относительно друг друга ча­стиц слоя и вводимого в него газа зависит не только от харак­тера движения слоя, но и от газораспределения. Движение газа в неподвижном и псевдоожиженном слоях широко исследова­но рядом авторов. Развитие газовой струи в общем случае приводит к образованию неустойчивой поверхности раздела слоя с областью газового пузыря, его отрыву и зарождению нового. В зависимости от параметров истечения меняются раз­меры и частота зарождения пузырей, а также интенсивность циркуляции через них твердых частиц. Различают три режима истечения газа: фильтрационный, пузырьковый и струйный, оп­ределяемые характерным соотношением размера факела и вы­соты слоя над ним [117].

При фильтрационном режиме размер отрывающихся пузы­рей настолько мал, что соизмерим с каналами между частица­ми, а частота отрыва настолько велика, что течение газа прак­тически непрерывно и не влияет на движение частиц. При об­разовании каверны или факела в них возникает циркуляция твердых частиц, что резко увеличивает интенсивность контак­та газовой и твердой фаз. Интенсивность внедрения частиц в факел ослабевает по длине струи, вследствие уменьшения разности давлений в слое и в струе и увеличения степени насы­щения струи частицами. При заполнении сечения струи части­цами наступает полное насыщение, после чего внедряющиеся в факел частицы, сталкиваясь, вновь входят в слой, образуя сплошную прослойку, служащую границей раздела [118].

Математическое описание этой сложной картины возможно лишь при ряде допущений и выделении отдельных составляющих процесса. Рассмат­ривались [1191 внутренняя задача, т. е. гидродинамика и процесс переме­шивания внутри индивидуальных струйных факелов с учетом наличия в них взвешенных частиц, а также внешняя задача — влияние струй на гидроди­намику и процессы переноса в плотной фазе слоя вне факелов [119]. Реше­ние задачи газораспределения в неподвижном слое базируется на рассмотре­нии равновесия сил, действующих иа выделенный элементарный объем ии - фильтруемого слоя, и определении критических расходов газа, отвечающих условию зарождения каверны [117]. Далее методами теории аналитических функций найдено поле давлений в окрестности струи. Разработанная мето­дика расчета параметров струи предполагает постановку единичного экспе­римента по пробою слоя для определения коэффициента, характеризующего интенсивность нарастания толщины струи в слое данных параметров. Таким образом, практическое использование разработанной теории сводится к про­ведению экспериментальных исследований в модельных условиях.

При чисто эмпирическом подходе к расчету струй [120] рассмотрено распространение газа в неподвижном и псевдоожиженном слоях в условиях адсорбции, т. е. при поглощении газа. Установлено, что наиболее интенсив­ный массообмен газа со слоем происходит в пределах факела. Показано влияние на массоперенос соотношения диаметров частиц и сопла. Отмечает­ся, что в условиях адсорбции динамическая и концентрационная границы факела совпадают.

Для описания струйного течения в псевдоожиженном слое используются методы интегральных соотношений [117]: уравнения интегрального баланса импульса, энергии и объема. При некоторых дополнительных предположени­ях о профилях скорости газа по оси и в сечениях основного участка, струк­туре потока в нем и законе нарастания толщины факела вдоль потока полу­чены основные кинематические, энергетические и массовые характеристики развития струй в псевдоожиженном слое. Такой подход также не лишен не­достатков, так как применим в пределах принятых допущений и только для условий, в которых получены значения эмпирических коэффициентов.

Исследование развития струи газа во вращающемся в бара­бане слое [121, 122] показало влияние на режим истечения ско­рости и плотности истекающего из сопла газа, а также давле­ния над соплом, режима движения материала и соотношения размеров частиц и сопла. В зависимости от этих параметров газ может истекать в режиме фильтрации или каналообразо - вания. Последний непригоден из-за больших проскоков газа. Режим фильтрации может быть как с образованием факела у сопла, так и без него. С возрастанием скорости истечения

у погруженного сопла вначале образуется шаровая каверна с циркуляционным движением частиц внутри нее, а затем — практически свободный от частиц факел.

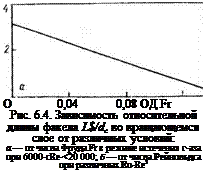
Анализ размерностей параметров, влияющих на относитель­ный размер замкнутого факела, определяемый соотношением его длины и максимального диаметра, показал, что эти пара­метры можно объединить в следующие безразмерные комп­лексы: Re, Eu, Fr, d/dc. Экспериментально определенные зави­симости размера факела от некоторых из безразмерных пара­метров приведены на рис. 6.4.

Зависимость длины факела (Ьф в м) от параметров истече­ния газа и вращения барабана выражается уравнением:

£Ф=</сг(1 — 4,9Fr)Re3S/4-10erfA (6.7)

где Re=vdjv— число Рейнольдса для истечения из сопла диаметра dc, v — скорость истечения газа, м/с; v — кинематическая вязкость газа, м2/с; d — диаметр частиц слоя, м; P=EuRe2 — безразмерный комплекс давления; Fr= = co2Z)/2g — число Фруда для барабана; to, D — угловая скорость (в с-1) и диаметр (в м) барабана.

Уравнение (6.7) справедливо в диапазоне изменения пара­метров: d/dc=0,05—0,3; L^dс = 3—10; Fr=0,01—0,16; />=400— 8000.

Исследование аммонизации гранул в режиме факелообразо - вания показало, что из-за создания разрежения в устье сопла подсасываются наиболее мелкие частицы, которые быстро ам­монизируются, перегреваются и налипают на сопло. Это приво­дит к нарушению процесса, образованию комков, изменению аэ­родинамики струи. Для предотвращения этих явлений скорость газа рекомендуется поддерживать в режиме начала факелооб - разования, т. е. при соотношении L^/dc=3, а для уменьшения скорости использовать сопла диаметром свыше 10d.

Истекающая из погруженного в слой сопла струя газа раз­вивается в зернистом слое и выходит на поверхность, причем тепломассообмен между газом и твердым материалом происхо-

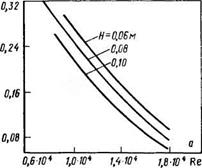
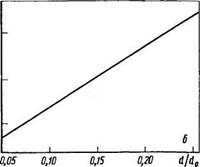
Рис. 6.5. Зависимость параметра истечения газа о из сопла от различных уело-

вий:

а — от числа Рейнольдса Re при d(dc =0,25 н различной высоте слоя И; 6 — от соотно-
шения размеров частиц и сопла d{dc при высоте слоя Я=80 мм и Re=8000

дит не только в факеле, но и в зоне фильтрации. Исследование зоны распространения газа в движущемся слое показало, что расширение газа происходит по параболическому закону, и его зону фильтрации через слой можно принять в виде параболои­да вращения с вершиной у погруженного сопла и основанием на поверхности слоя. Для неподвижного слоя это подтверждено другими исследователями [123, 124].

Экспериментально определялся параметр а параболоида, описываемого уравнением у—ах2, в зависимости от скорости истечения газа, частоты вращения барабана, диаметра частиц слоя, глубины погружения сопла. Зависимости а от числа Рей­нольдса и соотношения размеров частиц и сопла приведены на графиках (рис. 6.5). Как видно из графиков, значения о возра­стают с уменьшением высоты слоя. Установлено, что аммониза - цию предпочтительнее осуществлять в верхней скатывающейся части вращающегося слоя, высота которой составляет 0,06— 0,1 м. Следовательно, для расчета реальных процессов приве­денных данных вполне достаточно.

Зная параметр истечения а, нетрудно найти объем зоны фильтрации газа в слое зернистого материала:

У,,, - я//2/2с, (6.8)

где Н — глубина погружения сопла в слой.

Однако это справедливо лишь для инертного материала. При взаимодействии газа и твердых частиц, сопровождаемом массообменом, такая конфигурация газовой зоны - нецелесооб­разна, поскольку велика площадь истечения газа из слоя, что приводит к большим проскокам непрореагировавшего газа. Наиболее рационально иметь в слое замкнутый газовый объем, что достигается при определенном соотношении объемов исте-

кающего и поглощаемого газа. Такую задачу можно решить только зная скорость поглощения газа, т. е. кинетику аммони - зации продукта.