ФИЗИКА ПЛАЗМЫ

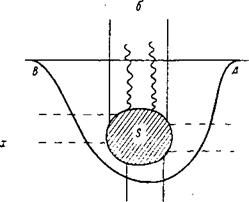
ЖЕЛОБКОВЫЕ КОЛЕБАНИЯ РАЗРЕЖЕННОЙ ПЛАЗМЫ С НЕКОМПЕНСИРОВАННЫМ ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ. II

А. В. Тимофеев

Показано, что при достаточно большой величине пространственного заряда и монотонном распределении электрического поля собственные колебания отсут­ствуют. Этот результат получен с использованием квазиклассического прибли­жения и поэтому применим к мелкомасштабным колебаниям, локализованным во внутренней части плазмы.

Введение

Настоящая работа продолжает исследование желобковых колеба­ний разреженной плазмы с некомпенсированным пространственным зарядом, начатое автором в работе [*J. В [*] было обнаружено, что собственные колебания плазмы могут отсутствовать, если радиаль­ное электрическое поле меняется линейно с расстоянием. Доказа­тельство основывалось на применении соотношений неопределенно­сти, аналогичных квантовомеханическим. Использовалось также то обстоятельство, что в реальных устройствах ларморовский радиус заряженных частиц имеет хотя и малую, но конечную величину. При отсутствии собственных колебаний методом преобразования Лап­ласа решалась временная задача с начальными данными.

В настоящей работе более общими методами показано, что отсут­ствие собственных колебаний характерно для систем с переменной в пространстве скоростью движения плазмы (Slipping system). Уст­ранение собственных колебаний можно рассматривать как стабили­зацию плазмы, поскольку в работе [*] показано, что в этом случае произвольные начальные возмущения затухают со временем. (По этому вопросу см. также f2]). Условие стабилизации разреженной

Плазмы Р2^~~^ по порядку величины совпадает с определенным-

Экспериментально!3] (здесь р = п°{ ~~ 1—величина раскомпен-

П0

Сации пространственного заряда; rd — дебаевский радиус ионов; R — средний радиус кривизны силовых линий магнитного поля; а — характерный поперечный размер системы). То же условие было по­лучено в [4а| при помощи качественных оценок, см. также [4б]. В этих работу само существование собственных колебаний принималось без осуждения, а стабилизация понималась как переход комплекс­ных собственных частот в действительные. (Аналогичное предполо­жение сделано в работах I5]). Однако в режимах, которые по [4* 5] являются стабилизированными, с необходимостью появляются резо­нансные точки, в которых фазовая скорость волны совпадает со ско­ростью невозмущенного дрейфа плазмы. Такие резонансы не учиты­вались в [4*5], между тем более корректное рассмотрение приводит в этом случае к выводу об отсутствии собственных колебаний.

Этот вывод получен с использованием квазиклассического при­ближения. Поэтому наше рассмотрение, вообще говоря, не исключает возможности существования собственных колебаний с длиной волны порядка характерных размеров плазмы, а также собственных коле­баний с малой длиной волны, локализованных в центре системы или у края плазмы, если к нему приближена металлическая стенка.

Следует отметить, что наши результаты могут быть использованы при исследовании устойчивости плоско-параллельных течений иде­альной жидкости, поскольку дифференциальные уравнения, описы­вающие возмущения такого течения, совпадают с исследованными в настоящей работе.

1. Основные уравнения

Для рассмотрения желобковых колебаний плазмы низкой плотно­сти с дебаевским радиусом ионов, много большим ларморовского (г*^>г, ), могут быть использованы уравнения двухжидкостной гид­родинамики и уравнение Пуассона для электрического поля. Учи­тывая, что частицы в возмущениях потенциала <р2 дрейфуют со ско­ростью У1 = -£-[1^<р1], и используя уравнения непрерывности и

Уравнение Пуассона, для самосогласованных возмущений потенци­ала <р1 нетрудно получить следующее уравнение I1* 41

(1)

Здесь У*—плазменная частота частиц сорта /; 2у =

= —I — циклотронная частота; У0. = -=- <р'0 (х)— *—начальная

/ПуС ■“

Скорость дрейфа в скрещенных полях — электрическом и слабонеод­нородном магнитном, радиус кривизны последнего Я; е^. — средняя энергия частиц сорта / обычно в экспериментальных устройствах, например, в адиабатических ловушках; Возмущения потен­

Циала выбраны в виде срх (х)е~ш+*ку. Ось 02 направлена вдоль маг­нитного поля, по 02, ОУ система предполагается однородной.

Как известно, желобковые колебания (кя = 0) могут быть неустой­чивы, если магнитное поле спадает в ту же сторону, что и плотность

Плазмы (Д>0 при-^-<о), а плазма не слишком разрежена

(га = -^|-^аД, здесь а« —см., например, I4]). Мы рас­смотрим* именно такой случай. Будем также считать, что начальное электрическое поле создается некомпенсированным пространственным

Зарядом, долю которого обозначим через р, р = ^ ^• Для

Определенности положим гс0; > п0в, такое соотношение между плотно­стью зарядов часто самопроизвольно устанавливается в адиабатиче­ских ловушках.

Уравнение (1) удобно рассматривать как одномерное уравнение Шредингера с полной энергией Е = — к2 и эффективным потенциа­

Лом

Будем считать для простоты, что как плотность плазмы так и плот­ность пространственного заряда спадают наружу монотонно. В этом

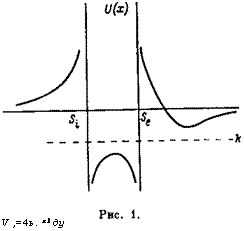
Случае характерная зависимость эффективного потенциала от коор­динаты х имеет вид, представленный на рис. 1.

Если электронная плотность превышает ионную, то общий вид и (х) сохраняется, меняется лишь порядок точек 5^,

Определенный интерес представляют также колебания однокомпонент­ной плазмы. В этом случае, используя уравнение Пуассона для невозму­щенного потенциала?0(х) и вы­ражение для начальной скорости дрейфа К0, удобно привести урав­нение желобковых колебаний к следующему виду

?1 = 0. (2)

Уравнение (2) описывает так­же колебания плоскопараллель­ного течения идеальной жидкости (см., например, Iе]).

В последнем случае под срх следует понимать функцию тока, связанную с возмущениями ско­рости соотношениями

—

Дх

■V

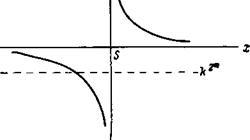
Зависимость эффективного потенциала в уравнении (2) от коорди­наты х показана на рис. 2. *

Эффективный потенциал и (х) действительно имеет вид, подобный изображенному на рис. 1, 2, если найдутся резонансные точки

Определяемые равенством - р =

Получим условия, при кото­рых следует ожидать появления резонансов. Из уравнения (1) сле­дует, что при наличии частиц с противоположным знаком за­ряда эффективный потенциал мо­жет быть отличен от нуля за счет разности в скоростях дрейфа

Счет разности в значениях плот­ности заряженных частиц п0{ —

— пАв^рп0.

Последний фактор оказывается важнее, если доля некомпенсиро­ванного пространственного заряда достаточно велика

.^'5

Если выполняется это условие, то локализованные собственные решения с ка^> возможны только при наличии резонансов. Дей­ствительно, в обратном случае для и (х) по порядку величины имеем

[/ (х)»к2. При этом уравнение (1) сводится к уравнению «сво­бодного движения»

Аналогичные соображения показывают, что при рассмотрении ко­ротковолновых колебаний однокомпонентной плазмы также необхо­димо учитывать резонансные точки.

В дальнейшем мы ограничимся только коротковолновыми колеба­ниями (ka^> 1), при исследовании которых допустимо применение квазиклассического приближения.

2. Сингулярные точки поворота, отсутствие собственных колебаний с Imco = 0.

Из рис. 1, 2 следует, что если уравнения (1), (2) имеют собствен­ные функции, то их область локализации по крайней мере с одной стороны ограничивается точкой, в которой U (х) обращается в беско­нечность. Следуя [7J, мы будем называть такие точки сингулярными точками поворота. В работах [7| они изучались в неоднородной по­коящейся плазме.

Для того чтобы продолжить решение через сингулярную точку, в [7] использовалось то обстоятельство, что вблизи от такой точки дифференциальное уравнение для возмущения можно записать в сле­дующем простом виде

+ (4)

Оно имеет решения J(x — x3)Z1[2 jA(x — х$], здесь Z1—функция Бесселя индекса «единица». Примем для определенности 0.

Тогда слева от S будет расположена область непрозрачности, в ко­торой 9j должно выражаться в виде комбинации функций Бесселя от мнимого аргумента. Справа, т. е. в области прозрачности, реше­ние должно быть выражено через функции Бесселя действительного аргумента. Связь между коэффициентами в этих комбинациях опре­делялась в [7] из условия непрерывности решения в сингулярной точке (х = х5). При этом возникала трудность, связанная с неодно­значностью функций Бесселя. Так, например, функция К2, спадаю­щая слева от S, имеет при x = xs логарифмическую точку ветвления (см., например, [8]). Нужная ветвь логарифма в [7] отбиралась из ус­ловия поглощения волны, падающей справа на S. Для этого требо­валось принять вполне определенное правило обхода точки S в пло­скости комплексного переменного z (cpj (z) является аналитическим продолжением ^(х))-

Переходя затем к большим значениям х — х8 |, х — х$|^>А-1, когда справедливы асимптотические выражения для функций Бес­селя, можно найти, что волна, бегущая в области прозрачности к точке S, слева от нее переходит в экспоненциально спадающее решение. При этом отраженная волна полностью отсутствует

(х — ха)'1' ехР [—2 V А Iх — xs | ] ^ (х ~ xa)‘U ехР ~2i V А (х — ^s)] • (5)

Здесь в соответствии с общепринятой традицией для величины - — может быть использовано обозначение к% =--- —----------------------------------------------------------------------- . На-

X Xs X Xs

Правление распространения волны, о котором говорилось выше, опре­деляется временной зависимостью решения e~*Mt и знаком экспо­ненты в правой части (5).

Соотношение (5) было получено в [7] при обходе точки S снизу. Если обходить S сверху, получается обратный результат, а именно, решение, спадающее слева от S, переходит справа от нее в волну, бегущую направо. Другими словами в этом случае волна излучается сингулярной точкой. Нотрудпо также найти, что при А<^0

© 2 Журнал технической физики, 1, 1968 г.

По f7] сингулярная точка по-прежнему должна обходиться снизу. Следует отметить, что в случае, рассмотренном в [7], направление обхода S может быть определено по Ландау добавлением к частоте малой положительной мнимой части *v.

Поведение второго независимого решения, растущего в области непрозрачности, исследовано в [7] не совсем корректно. Этот вопрос будет обсужден ниже.

Мы получим аналогичные результаты более простым способом. Известно (см., например, [*]), что смена асимптотических представле-

%

Ний решения происходит на линиях Стокса, на которых Re J kxdz = 0.

*s

Для уравнения (4) — это линии, выходящие из точки S, аргумент которых равен arg (z—хя)==0, ±2тг, ±4тс,. .. Поэтому на плоскости комплексного переменного 0^|arg(z—xs) | ^ 2г для решения можно использовать одно и то же асимптотическое представление. Так, на­пример,[функция Кх (2) (где Z = 2J A (z — х8) при 2^> 1,| arg(z—х3) |<]3и) может быть представлена следующим асимптотическим выраже­нием: Кг(2)ж — (^гУ*е~2 (СМв» например, |8]). Это позволяет сразу пе­рейти от больших положительных значений х—xs к отрицательным, если только известно, какая ветвь функции К1 (2) должна представ­лять решение, или, иными словами, определено положение разреза, выходящего из точки ветвления z = xs. Следуя Ландау, мы внесем в этот вопрос определенность, заменив со на ш-f-iv. При этом в на­шем случае [см. уравнения (1), (2)] z — ха переходит в z — ха—.

Следовательно, если kVо>0, то полюс смещается с действительной оси вверх и соответственно разрез должен пройти в верхней полу­плоскости комплексного переменного z. При kV[|<0 разрез следует провести в нижней полуплоскости. (Напомним для сравнения, что в [7], где рассматривалась покоящаяся плазма, сингулярная точка об­ходилась снизу).

Теперь, воспользовавшись асимптотическим представлением для функции Кг(2) при &Fo>0, сразу приходим к формуле (5). Если kVо<0» то знак в показателе экспоненты в правой части (5) должен быть заменен на противоположный.

Если, как это сделано в [7], не проводить различия между реше­ниями, спадающим и нарастающим на линии Стокса arg (z — z$) = 0, то, продолжая последнее, можно было бы получить сходные резуль­таты. Однако, как следует из общей теории асимптотических представ­лений [9], с нарастающим решением нужно обращаться более осторожно. Действительно, на линии Стокса погрешность в асимптотическом пред­ставлении нарастающего решения, вообще говоря, превышает по вели­чине спадающее, поэтому коэффициент при последнем не может быть определен однозначно. Однако в области прозрачности оба решения при соответствующей нормировке дают волны одинаковой амплитуды, бегущие в разные стороны. По этой причине не существует однознач­ного продолжения нарастающего решения в область прозрачности. Это, однако, не мешает однозначному продолжению решения в обратном направлении.

Учитывая вышесказанное, для решения уравнения (4), нарастающего в области непрозрачности, запишем формулу связи в следующем виде

(I — х3)Ч> ехр [2 V Ax — xs\ *- (I — XS)'I - exp [2 г У А(х — is)]. (6)

Эта формула связи, так же как и (5), может быть использована при анализе уравнений (1), (2), если kV’Q"> 0.

В обратном случае (Л^<^0) знак в показателе экспоненты в правой части (5), (6) следует заменить на противоположный.

Теперь нам нетрудно показать, что уравнения (1), (2), с эффектив­ным потенциалом, изображенным на рис. 1, 2, не имеют локализован­ных собственных функций.

Рассмотрим сначала уравнение (1). В этом случае локализованные решения, если такие существуют, ограничены 6 обеих сторон сингуляр­ными точками поворота. Пусть для определенности кУ’0^>0; тогда в соответствии с (5) решение, спадающее слева от 5,-, справа от этой точки переходит в волну, бегущую налево. Это решение нельзя сшить с решением, спадающим справа от £#, т*ак как последнее слева от Бв переходит в волну, бегущую направо.

Точно так же невозможны локализованные решения и для потен­циала, показанного на рис. 2.

Действительно, решение, спадающее за обычной точкой поворота, переходит в области прозрачности в стоячую волну (см. например [9]), в то время как решение, спадающее за сингулярной точкой поворота, переходит в бегущую волну.

Настоящее доказательство основано на возможности квазиклассиче - ского представления решения в области между точками поворота. Для уравнений (1), (2) это условие может, вообще говоря, не выпол­няться. Это ограничение будет устранено нами в следующем разделе.

3. Отсутствие собственных колебаний с произвольным значением 1тш = у

Рассмотрим теперь вопрос о существовании собственных колебаний с более общих позиций. Обратим внимание на то обстоятельство, что

Эффективный потенциал и (г) в уравнениях (1), (2) спадает как ——

2 — 2 в

При удалении от сингулярных точек. Это непосредственно видно для

У

Уравнения (2). Что касается уравнения (1), то оно для | ъ = | ^

Г2

Сводится к уравнению (2). При этом необходимо учесть, что

Пр

Для | 2 — г можно пренебречь разностью в скоростях дрейфа

V TOC o "1-5" h z О

Электронов и ионов. Именно поэтому в вышеприведенном условии мы

Г2

Опускаем индекс ; у величины ъау Следовательно, при ъ —

V" (г) Р

Эффективный потенциал и (г) имеет вид ■■—- и по порядку

У — у о 2з)

Величины равен и (г) ~а 2 ^. В результате при достаточном уда­лении от сингулярных точек, когда г — 25 | (ак2)'1, уравнения (1), (2)

принимают следующий простой вид

О)

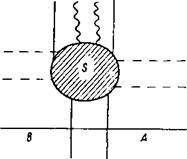
Теперь полезно обратиться к рис. 3, а, б. На них заштрихована область Я, в которой эффективный потенциал превышает по порядку величины к2, и следовательно, уравнения (1), (2) отличаются от (7). На рис. 3 изображены линии действительной фазы — сопряженные линии Стокса (сплошные линии), линии мнимой фазы — линии Стокса (штриховые линии) и разрезы (волнистые линии). Эти линии, согласно п. 2 (см. также [*]), выходят из точек поворота. Их число и положение
даны на этих рисунках условно. Для нас важно лишь то обстоятельство,

Г

Что вне области £ линии действительной фазы ^1ш^кхс1г — 0^ идут

Ж

Вертикально, а линии мнимой фазы ^Ие = 0)—горизонтально.

Разрезы выходят из сингулярных точек поворота и идут по направ­лению вверх при 0 и вниз при кУ0<^0 (см. раздел 2).

В соответствии с правилом обхода сингулярностей по Ландау на­правление разрезов должно оставаться неизменным при произвольных 1та> = у. Поэтому при т<0 разрезы должны пересечь действительную ось, и в этом случае решение, если оно существует, должно на дей­ствительной оси быть разрывным. При этом точка, в которой разрез

Пересекается с действительной осью, остается неопределенной, и, следовательно, решение не может быть определено однозначно. По этой причине мы можем утверждать, что уравнения (1), (2), дополненные правилом аналитического продолжения решения по Ландау, не могут описывать затухающих колебаний реальных систем. В случае плоско­параллельных течений реальной жидкости решение остается непрерыв­ным и однозначным, так как уравнение (2) в том секторе комплексного переменного, где могут проходить разрезы, дополняется членами с высшими производными, которые учитывают вязкость [8]. В случае колебаний разреженной плазмы (г4^>гл ) аналогичные эффекты слишком ничтожны, чтобы их имело смысл учитывать. Впрочем, как будет видно из дальнейшего, возможно независимое доказательство отсут­ствия собственных решений с ^<0 у уравнений (1), (2). При этом конкретный вид решения в секторе комплексного переменного, содер­жащем разрезы, окажется для нас несущественным.

Приступим к такому доказательству. Для этого рассмотрим область,

Лежащую справа от 5. В этой области решение, спадающее к границе

Плазмы, имеет вид я1—е~к*. Продолжим это решение налево от 5 по

V' о

, то, как следует из рис. о, а, при этом мы

Не пересекаем линий Стокса, и, следовательно, вид решения не должен измениться. Поэтому слева от 5 решение должно нарастать.

Это представление может измениться за счет добавления спадающей экспоненты. В нашем случае в области справа от £ нарастающее решение отсутствует, и поэтому из условия непрерывности асимпто­тическое представление решения остается неизменным. При переходе через сопряженную линию Стокса решение <р1 = е~к* становится нарастающим.

Поднимаясь затем на действительную ось, мы вторично пересекаем линии Стокса. При этом к нарастающему решению может быть добав­лено спадающее. Однако слева от Б им можно пренебречь. Таким образом, мы приходим к выводу, что ни при каком значении ^ нельзя построить решения, спадающего в обе стороны от Я.

Это доказательство пригодно при произвольных положительных

Значениях у, а также при т<С0» если - т4г - В обратном случае,

I * ' о I

Когда I | 1, оно применимо лишь для определенных распределе-

О

Ний У0(х). Действительно, при |~т-|^>1 особая точка а с нею и

Область Я на рис. 3, б смещаются с действительной оси далеко вниз на расстояния, много большие а. Между тем для распределений началь-

-‘1 V" (г)

Ной скорости типа У0(г)~-е а% отношение у ) неогРаниченно

Возрастает при 1т2->оо. Поэтому на линии АВ уравнения (1), (2) уже не сводятся к уравнению (7).

Впрочем существование решений с 1 представляется мало-

| л к о

Вероятным, поскольку в настоящем случае кУ0 является наибольшей величиной, имеющей размерность частоты.

Остановимся теперь на ограничениях, связанных с использованием квазиклассического приближения.

Во-первых, размеры области Я, в которой С/ (г)^А:2, должны быть много меньше характерного размера системы, т. е. величины а. Оче­видно, что это верно лишь для мелкомасштабных возмущений с ка^> 1. Во-вторых, квазиклассическое приближение должно быть справедливо как справа, так и слева от Я. Это означает, что сингулярные точки должны быть удалены как от центра плазмы, так и от ее края, если к последнему приближена металлическая стенка. В обратном случае сингулярная точка может совпасть с краем плазмы или с ее центром, т. е. с точками, в которых решение должно обращаться в нуль. Такие решения должны рассматриваться особо.

Как уже отмечалось, уравнение (2) совпадает с дифференциальным уравнением для возмущенной функции тока плоско-параллельного течения идеальной жидкости. Для этого случая известна теорема Рэлея [®], утверждающая, что собственные колебания с отсут­

Ствуют, если профиль скорости течения не имеет точек перегиба

М^(*о) = 0).

Наши результаты могут рассматриваться как обобщение этой тео­ремы на случай произвольных у для квазиклассических возмущений во внутренней части жидкости.

Таким образом, мы показали, что если электрическое поле доста­точновелико [выполнено условие (3)] и меняется монотонно (У'0~ Е'о=^=0), то собственные колебания, локализованные во внутренней части плазмы, отсутствуют. В этом случае для рассмотрения вопроса о временной эволюции начальных возмущений электрического потенциала необ­ходимо непосредственное решение задачи с начальнымн данными. Оказывается (см. [1,21), что элементарными решениями, по которым нужно разлагать начальные возмущения, являются в этом случае моду­лированные пучки заряженных частиц, дрейфующие в начальном элек­трическом поле.

Эти пучки аналогичны так называемым волнам Ван-Кампена (неана­литические решения Ландау) для колебаний однородной покоящейся плазмы [10]. В работах 11>2| показано, что любое гладкое возмущение, созданное совокупностью модулированных пучков, затухает во времени,

И, следовательно, плазма является устойчивой.

За обсуждение работы автор благодарен Б. Б. Кадомцеву, Ю. Н. Днестровскому и Д. П. Костомарову.

ПРИЛОЖЕНИЕ

В разделе 2 мы нашли, что при продолжении решения через син­гулярную точку поворота его поведение определяется формулами (5), (6). Покажем, что эти соотношения не изменяются при учете конечной величины ларморовского радиуса заряженных частиц.

Уравнения, учитывающие этот эффект, были получены в работе [х] [(ср. с (1). (2)]

(777: X..... <1Л>

Здесь скобки означают усреднение по величине ларморовского

Радиуса. При у — 1 >> I выражение (1.1) переходит в (2). (Для

Простоты рассматриваются колебания однокомпонентной плазмы).

Рассмотрим решение, спадающее в области непрозрачности. В окрест­ности особой точки оно имеет вид

Ср1 = 2 у/Ах Кх (2 у/Ах)« 1 — (Ах) 1д (Ах). (1.2)

V*

Здесь Л = ~>0, А~1^>х^>гх , х>0. Начало координат выбрано в ре - зонансной точке.

Это решение из-за неоднозначности логарифма может быть продол­жено в область отрицательных х различными способами. Как и в раз­деле 2, для устранения неоднозначности будем следовать Ландау,

Заменив в (1. 1) со на <о4-Ь. При этом в (1.2)л’х->х— 4тт - (для апре­ле V о

Деленности полагаем &7']>0).

Проинтегрируем уравнение (1.1) по действительной оси в симме­тричных пределах (от х — —е до х = е, А~х^> гх ) относительно точки х = 0. В этой области с точностью до величин порядка Агя 1 можно положить ср1»1. Тогда этот интеграл определяет скачок про­изводной при переходе через особую точку

*|"=ЧГ? гЬг,'У (,'3)

-ГЛ.

Здесь учтено, что интегралы от —е до —гя и от гя до е взаимно сокращаются, а также изменен порядок интегрирования по йх и усред­нения по ларморовскому радиусу.

? йх

Интегрирование по йх дает I — ■ — =—Ы. Усредняя

-I ,

По ларморовскому радиусу, окончательно получаем ср' |*в = Следо­вательно, при х < 0 А~г^х^> гя решение (1.2) должно быть опре­делено как

—(i4i)llg(i4|i|)-finj. (1.4)

Продолжая теперь выражения (1.2), (1.4) в область больших зна­чений |х|, где справедливы асимптотические представления, снова при­ходим к выражению (5).

Заметим, что в случае максвелловского распределения усреднение по гя можно произвести непосредственно в уравнении (1.1)

^ - F*2+тй:£ ^ ^ (1 + - й" | e,,rfp)] *=°- V■ 5>

Здесь Z — ~ . Нетрудно видеть, что, интегрируя (1.5), мы

Г 1.л " о

Приходим к тому же самому результату: <р[|*_t = inA.