ТРАНСФОРМАЦИЯ МАГНИТОЗВУКОВЫХ КОЛЕБАНИЙ ПРИ АЛЬФВЕНОВСКОМ РЕЗОНАНСЕ
В квазиклассическом приближении рассчитан коэффициент трансформации магнитозвуковых колебаний в электронные при альфвенов - ском резонансе в неоднородной замагнпченной плазме. Вместе с проведенным ранее анализом длинноволновых колебаний результаты данной работы позволяют составить полное представление о зависимости коэффициента трансформации от параметров плазмы и колебаний. Результат^ аналитических расчетов хорошо согласуютья с численными, которые также проводились в настоящей работе.
Введение
Электромагнитные колебания, распространяющиеся по неоднородной плазме, могут испытывать «локальные» резонансы, проявляющиеся в резком уменьшении длины волны. Характерными примерами резонансов являются гибридный резонанс (ГР) необыкновенных колебаний (НК) и альфвеновский резонанс (АР) магнитозвуковых и альфвеновскых колебаний (МЗК и АК) [1]. В окрестности резонансной точки электромагнитные колебания трансформируются в колебания с меньшей длиной волны (МЗК и АК — в «электронные» колебания (ЭК), НК — в бернштейнов - ские) *. Мелкомасштабные колебания весьма эффективно поглощаются плазмой, поэтому наличие резонансных точек в плазме позволяет использовать крупномасштабные электромагнитные колебания для ее нагрева. Эффективность нагрева определяется коэффициентом трансформации крупномасштабных колебаний в мелкомасштабные. В настоящей работе рассчитывается коэффициент трансформации МЗК в ЭК при АР [85]. Ранее в [5] он был определен для МЗК с длиной волны, значительно превышающей как размер области непрозрачности МЗК в окрестности точки АР, так и размер области прозрачности АК (рис. 1). В этой же работе проведены численные расчеты коэффициента трансформации для несколько большей области параметров. Нами рассматривается другой предельный случай коротковолновых — «квазиклассических» МЗК. Используется аналогия между ГР и АР, благодаря которой коэффициент трансформации НК в бернштейновские колебания при ГР, найденный в [6], по виду оказывается идентичным коэффициенту трансформации МЗК в ЭК при АР. В [6] рассматривались колебания плоского слоя плазмы с 0. Такие колебания соответствуют аксиально-симметричным модам цилиндрического плазменного шнура. Нами показано, что выражение, полученное в [6], остается справедливым и для колебаний с Ny¥=0. (Рассмотрение в этом случае усложняется из-за появления так называемых фиктивных сингулярностей [7, 8].) Проанализированы также низкочастотные колебания, коэффициент трансформации которых отличается от найденного в [6].
|
N1 |
![]()
|
А |
![]()
|
МЗК |
![]()
|
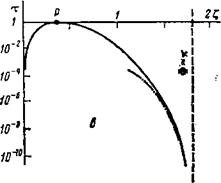
Рис. 1. Зависимость х-компоненты показателя преломления от координаты Х: а - Ny— 0, Б - #у=*0. Х8 - точка АР, в точках *1.* выполняется равенство Ъ—Nгг=x±g. Область прозрачности МЗК расположена слева от точки Х|(Х|/)У АК-между точками Х3 и Хг(хг'). Плотность плазмы спадает слева направо |
 Совокупность аналитических выражений коэффициента трансформации МЗК при АР, полученных для различных предельных случаев в [5] и в настоящей работе, позволяет составить полное представление о поведении коэффициента трансформации в зависимости от параметров плазмы н МЗК. Оно подтверждается числеплы - ми расчетами, которые также проводились в настоящей работе. При расчетах использовался метод дифференциальной прогонки, разработанный для решения дифференциальных уравнений с малым параметром при старшей производной [9, 10]. К данному классу принадлежат волновые уравнения, описывающие колебания плазмы при наличии АР. Результаты численных расчетов хорошо согласуются с аналитическими, причем согласие оказывается вполне удовлетворительным даже за пределами области применимости квазиклассического приближения, использовавшегося в настоящей работе при аналитическом рассмотрении.
Совокупность аналитических выражений коэффициента трансформации МЗК при АР, полученных для различных предельных случаев в [5] и в настоящей работе, позволяет составить полное представление о поведении коэффициента трансформации в зависимости от параметров плазмы н МЗК. Оно подтверждается числеплы - ми расчетами, которые также проводились в настоящей работе. При расчетах использовался метод дифференциальной прогонки, разработанный для решения дифференциальных уравнений с малым параметром при старшей производной [9, 10]. К данному классу принадлежат волновые уравнения, описывающие колебания плазмы при наличии АР. Результаты численных расчетов хорошо согласуются с аналитическими, причем согласие оказывается вполне удовлетворительным даже за пределами области применимости квазиклассического приближения, использовавшегося в настоящей работе при аналитическом рассмотрении.
1. Основные уравнения
Рассмотрим колебания плоского слоя плазмы в однородном магнитном поле.
Будем описывать их уравнениями двухжидкостной гидродинамики в форме, предложенной в [11],
(1)
1гВ+ (£,+£,) (-М'Е) =0,
|
<■>« |
![]() Где В, Е — 2-компоненты магнитного и электрического поля колебаний соответственно,
Где В, Е — 2-компоненты магнитного и электрического поля колебаний соответственно,
■1 +
“і««1
|
|
(оРІ — ленгмюровская частота частиц сорта 7=е, і, ш, — циклотронная частота, эффекты теплового движения частиц не учитываются, значки «перпендикулярно» и «параллельно» отмечают направление относительно основного магнитного поля. Используется декартова система координат с осью ОХ, направленной вдоль градиента плотности, и осью 02 —
вдоль основного магнитного поля. В (1) введена безразмерная координата X (ко/с-^х).
Нетрудно показать, что система (1) имеет единственную особенность в точке, где е=0. В зависимости от значения частоты данная особенность соответствует верхнегибридному или нижнегибридному резонансу, который испытывают НК. В простейшем случае Л^2=0 уравнения, составляющие систему (1), разделяются, причем НК описываются первым уравнением
В окрес/ности точки гибридного резонанса для регуляризации задачи необходимо учесть эффекты конечного ларморовского радиуса. При этом порядок волнового уравнения повышается до четвертого.
В области низких частот (а, когда выполняется условие |ен|^ >е, g, система (1) так же, как и в случае Nz=0, распадается на два уравнения. Первое из них имеет вид (2). Оно описывает крупномасштабные АК и МЗК. Второе уравнение
|
( |
Е—N *
Al+s,,-------- -^)Е=° <3>
Описывает мелкомасштабные ЭК.
Однако в отличие от случая NZ=О уравнения (2), (3) при NzҐ*0 независимы ЛИШЬ Приближенно, С ТОЧНОСТЬЮ ДО Членов Ttmjnii. Связь между этими уравнениями становится существенной в окрестности точки АР (e==iV,2) , в которой уравнение (2) имеет особенность. Для описания явления трансформации АК и МЗК в ЭК, происходящего в данной области, необходимо обратиться к исходной системе (1), что эквивалентно использованию уравнения 4-го порядка. В то же время, если нас не интересуют детали поведения АК и МЗК в окрестности точки АР, то эффект трансформации в ЭК можно учесть, оставаясь в рамках уравнения (2). Для
Этого при продолжении решения через точку АР следует использовать правило обхода Ландау. Данный прием будет использован ниже при аналитическом расчете коэффициента трансформации МЗК в ЭК. Таким же образом рассчитывался в [6] коэффициент трансформации НК в бернштей - новские колебания.
2. Аналитическое рассмотрение
А. Колебания с Nv=0. При рассмотрении колебаний с NV=О будем опираться на аналогию между низкочастотными (со<о>^) АК и МЗК с NZ^О и высокочастотными (cd^cd,) НК с Nz=0. Квазиклассическое выражение для показателя преломления последних, как известно, имеет вид iV*2= = (е*—£*)/е. В плазме с переменной плотностью зависимость Nx(X) аналогична изображенной на рис. 1, с тем отличием, что область большей плотности располагается с правой стороны рисунка. В [6] анализировалось падение НК со стороны меньшей плотности (из вакуума). При *«
Г*= J |IV,|Dx>L (выполнение этого условия естественно для квазиклас -
.•i
Сического случая) выражение для коэффициента трансформации в бернштейновские колебания в точке верхнегибридного резонанса, полученное в [6], можно представить в виде
Т=4е“2Г sin2 Ф. (4)
*«
Здесь Ф —* JiV. dx — набег фазы НК по внутренней области прозрачно - *1
Сти. Характерно, что при Ф=ля коэффициент трансформации обращается в нуль. В этом случае точка ГР приходится на узел колебаний, устанавливающихся во внутренней области прозрачности.
Б силу сходства зависимостей Nx(X) выражение (4) должно также давать коэффициент трансформации МЗК в ЭК в точке АР при падении со стороны большей плотности.
Отметим, что в [6] при построении квазиклассического решения область непрозрачности XiXB «проходилась» с помощью правила Джеффриса 3. В [12] показано, что использование этого правила законно лишь в низшем приближении по параметру ехр(—Г). Поэтому попытка учесть в выражении для т более высокие члены разложения поехр(-Г), сделанная в [6], может оказаться некорректной.
Б. Колебания с NvҐ[86]0. Покажем, что выражение для коэффициента трансформации (4) остается справедливым и в случае Ny^= 0. При Ny^O Точки поворота квазиклассическпх решений смещаются: Xlt 2. Точки же Хи 2 на первый взгляд становятся сингулярными точками уравнения (2). Действительно, в них, как и в точке хя, обращается в нуль коэффициент при старшей (второй) производной. Однако на самом деле этого недостаточно для возникновения особенности. Особая точка может оказаться фиктивной, если в ее окрестности разложения коэффициентов при первой и нулевой производных имеют некоторый специальный вид. Например, в окрестности точек Xit Г уравнение (2) сводится к следующему:
^ ^В-о.
Где I]=Ny(X—Xi, *). Оба независимых решения последнего уравнения ана - литичны в точке т|=0 и представляются в виде рядов по степеням Г:
В(,)=Цп+0(л3), Bu,=nl+0(V).
Таким образом, особенности уравнения (2) в точках Xti Г на самом деле являются фиктивными. Если это уравнение переписать для какой - то иной величины, например ЕУ, то фиктивные особенности в точках Xit Г Пропадут. Однако вместо них возникнут аналогичные фиктивные особенности в других точках [7, 8].
Обратимся теперь к анализу квазиклассических решений (2) при наличии фиктивных особенностей. При формальном расчете величина Nx в этих точках обращается в бесконечность. Слагаемое, приводящее к особенности Nx, содержит Производную ОТ Невозмущенных величин co(g/Z))*'. Данное слагаемое можно учесть через предэкспоненциальный множитель. С этой целью в области Х">х8 представим (2) в виде
Здесь все члены (2), ответственные за фиктивную особенность, сконцентрированы в первом слагаемом. Отметим, что последнее слагаемое регулярно в точке Х=хг и мало по параметру квазиклассичности ~ClNxl&, I — характерный масштаб изменения плотности плазмы.
В области прозрачности имеем
Я г
В«С, а+(х)ехр( i J N, dx) +Сга - (х) exp ( —* J N.Dx) , (6)
V
Где ЛГх=(1/а—iV„2)v а—(е— NX*)ID, функции А±(х) определяются уравнением
2(In <x*),'+(ln Nx)X'+(L±INjNx){N А)х=0, Из которого получаем
При Х-+хг (аУУ„2-*-1) имеем а^Л^Л^ехр(^Ьп/А). Поскольку в окрестности этой точки (2) сводится к уравнению Эйри, то в решении (6), соответствующем при Х>х2’ спадающей экспоненте, должно выполняться равенство Положив С 1=—г/2 и учитывая соотношение
А± х—*хоГ ехр (— ^л/^)’ находим, что при х—Х3 выражение (6) принима -
*х5 ет ВИД
£«Лг,''соз( | Д^х-Ф-лм).
В области Х^х8 наличие в (2) слагаемых, пропорциональных #„2, несущественно. Поэтому, как и в случае N„=0, решения уравнения (2) выражаются через функции Ханкеля //£1,2> (^(х—х3)Чг1гх1г)- Используя при продолжении через точку Х3 правило обхода Ландау (обходя при С1по1с1х<0 точку Хв в комплексной плоскости снизу) и определяя вид асимптотики в области Х<ха с помощью правила Джеффриса, получаем
* *
£*|ЛГ,|‘4 {-^-ехр(-I |лг,|сг1-гф)-зтфехр( I Лг. йх)} . (7)
*я *я
При продолжении решения к левой границе области непрозрачности Хх х8 необходимо учесть фиктивную особенность в точке я». Для этого представим (2) в виде, аналогичном (5),
Рассмотрим квазиклассическое решение вида
• Я
В=С, р+(х)ехр ( 1 |ЛГ,|Аг)+Сгр_(х)ехр(-| |ЛГ,|с*х), (9)
Где |ЛГ,|=(ЛГ„2—1/а)' Фупкдии 3*(х) определяются уравнением £(1п р1).'+(1п|ЛГ1|),'+(1±ЛГ,/|^|)(1па),'=0, из которого получаем
P±=(aiVv2(a^w2-l))-,Чa^2-1/2+(fl^2(^y2-l)),/,):p^
При Х-+х3 имеем р±-^=Р2^‘Аа( |Л^х|/А^у)Поэтому решение (9) принимает вид (7>, если С^Л^)7’зт Ф, С2=(ЛГ„/2)ъ ехр(—1Ф). Учитывая
Соотношение ~1 Г* ^ ('VI ^х) » в области Х~хх получаем
X *
Вх шк{51пФехр( I 1ЛГ-1*-г)+-^вхр(-1 |ЛГ.|Л:+Г-1ф)}.
В окрестности точки х/ фундаментальную систему решений (2) удобно взять в виде
Вх, 2~(х—Хх)~'и ехр{±г! аОх (Х—Хх)4*) .
Для таких решений постоянная Стокса, как хорошо известно [12], равна Продолжая решение через точку х/ с учетом правила Джеффри -
878
Х
В ~ ,■■{ (exp(Г—1Ф)— £зтФехр(—Г))ехр(« J NxDx+In/I^ +
2 |iV*l
— I
Я
+ (exp(r~iO)+isin Ф exp (—Г)) exp ( —i | Nxdx—in/4)}.
V
Из последнего выражения следует, что коэффициент отражения МЗК по мощности равен р=1—4е~2Г sin2 Ф-Ь0(е“4Г). Следовательно, учитывая закон сохранения энергии, находим, что коэффициент трансформации, как и в случае Nv=0, дается выражением {4).
В. Колебания при Ф<2. Выше считалось, что характерная длина волны колебаний мала как по сравнению с размером области непрозрачности (Г>1), так и по сравнению с размером области прозрачности АК (Ф>1). Обратный предельный случай длинноволновых колебаний (Г, Ф<1) рассматривался в [5]. Однако возможно такое соотношение параметров ПРИ котором квазнклассическое приближение непригодно лишь в области прозрачностп АК (Г>1>Ф). Рассмотрим этот случай.
При gcoo)-*-0 уравнение (2) в окрестности точки Х8 принимает вид
((X-Xs)-LBx')X'-Nv*(X-Xs)-LB=0.
Его решение, спадающее в области Х>х8, выражается через функцию Макдональда:
B=Nv(X-Xs)Kl(Nv(X-Xs)). (10)
Продолжим (10) в область x<xs, используя правило обхода Ландау (см. выше). В окрестности точки Хв сопряженные линии Стокса расположены при arg(x—Јs)=—я/2, —Зя/2, а постоянная Стокса равна 2I [13]. В соответствии с правилом Джеффриса на линии arg(x—xs)=—я имеем
B^((jil2)Nv(x—xa)Yl'(exv(-Ny(x--xs))+i exp(Nv(x—xs))).
Продолжая решение через область непрозрачности, в окрестности точки Xi находим
• •
B&Ny(ND/2E.I'N,)'L‘ (ехр(г —J |Agdr)+iexp(-r + J |W,|d*)).
X/
Переход через точку Xi совершается точно так же, как и в предыдущем разделе. В результате в области прозрачности (х<х{’) получаем
((«R-4-E"R)ExP(-^*^-T)+
К
TOC o "1-5" h z + («r + - i-e-r)exp(iJiV, rfx + ^-)). (И)
V
Из (И) следует
P^l-т, т=2ехр(—2Г). (12)
Найденное выражение для т не совпадает с пределом (4) при Ф-*0.
Расхождение, по-видимому, обусловлено тем обстоятельством, что (4)
Было получено в предположении ф»1.
Коэффициенты отражения и поглощения МЗК зависят только от двух величин: Гиф. Довольно простые выражения для этих величин удается яайти при когда как размер области непрозрачностн, так и раз
Мер области прозрачности АК малы по сравнению с характерным мас
Штабом изменения плотности плазмы I. Полагая Г—N1г^гx'(x—Xв)1 £=* =сопзЬ и опуская в выражении для Nxz малые слагаемые —Л^„с//со, получаем
Г= (^У«3/3|ех'|) (Н-6)7*( ((+Ь)'1г—)К(д)+2Е (<?)), (13)
Ф=(^з/з|е;|)(1+б),'‘(((1+б),'*+1)/1:(/?)-2£(/7)), (14)
Где
6=4^Д ^=1((1+6),/1+1)2-1(1+6)-,/*)7%р=(((1+6)7>-1)2-,(1+6)-,/,)'
К, Е — полные эллиптические интегралы.
При £-*-<» (|ЛГу| —*-0) из (13), (14) находим
В обратном предельном случае 6-^0 (#-^0) коэффициенты р, т зависят от единственной величины Г«2Л^3/3|ех'| (Ф-^0).
Из полученных выражений следует, что при N„-*-0 (£-*-<») квазиклас - сическое приближение применимо (Г, Ф>1), если (<ОрЛс) (а)/й)<)5/,>1. Нетрудно видеть, что данное условие может быть выполнено во многих современны* термоядерных установках. С увеличением размера системы и плотности плазмы, а также при переходе к колебаниям с достаточно большими значениями область применимости квазиклассического
Приближения расширяется.
В настоящем рассмотрении считалось, что энергия падающих МЗК распределяется по двум каналам: в отраженные МЗК и в ЭК, уходящие от точки АР. Из соотношений взаимности следует, что при падении ЭК на точку АР коэффициент отражения ЭК и трансформации в МЗК должны совладать с найденными выше. Вообще говоря, мыслима ситуация, по-ви - димому, не реализуемая в современном термоядерном эксперименте, когда АК также могут потреблять энергию (длина затухания сравнима или меньше их области прозрачности). В этом случае приобретают реальный смысл коэффициенты взаимной трансформации и отражения всех трех видов колебаний (МЗК, АК, ЭК) (см. Приложение).
3. Численные расчеты
Коэффициент трансформации МЗК рассчитывался также численно на основе решения исходной системы (1). Она содержит малый параметр е/|еп|<1. В пределе |е,||=°о система сводится к сингулярному уравнению второго порядка (2), описывающему МЗК и АК. Если |в„ | велик, но конечен, сингулярность устраняется, однако появляются коротковолновые «электронные» моды с характерной длиной волны, в (|е(,|/е),,я раз меньшей. В области непрозрачности слева от Ха одно из двух коротковолновых решений нарастает с большим пространственным инкрементом, что затрудняет прямое численное интегрирование. Для преодоления этой трудности использовался метод дифференциальной прогонки [9, 10]. Следуя этому методу, запишем (1) в виде
TOC o "1-5" h z (Ятх')*'=£т, (15)
‘ЧСТ д.)
Nt*
Подстановка Атх'*Лт+а переводит (15) в систему
А:=-АК-'А+Ь, (16)
Ах'------ АК~'&, . (17)
Хх’ *=К~1Ат+К~1а. (18)
Устойчивость интегрирования системы (16) —(18) определяется собственными значениями матрицы АК~{— Xit 2. Те же самые собственные значения имеет и матрица К~1А. Из однородного уравнения (18) Тх'—К~1Ах Следует, что в области применимости квазиклассического приближения они связаны с волновыми числами собственных колебаний соотношением X~iNx. Чтобы избежать появления быстро нарастающих электронных мод на левой границе области интегрирования х_, матрица А выбиралась такой, чтобы однородное уравнение (18) описывало экспоненциально спадающие ЭК и убегающие от точки Ха МЗК. Эти колебания могут «завязаться» с нарастающими ЭК лишь в точке трансформации Ха. Поэтому уравнения (16), (17) устойчиво интегрируются от х_ до Ха (прямая прогонка), а (18) - от Xs К X- (обратная прогонка). Аналогичным образом на правой границе Х+ матрица А выбирается так, чтобы в этой области однородное уравнение (18) описывало экспоненциально спадающие АК и убегающие от точки Ха ЭК. При этом прямая прогонка осуществляется на интервале (х+, Ха), обратная — на (Х8, х+).
Посредством величины A в задачу вводятся волны, падающие на область трансформации. В интересующей нас задаче неоднородный член K~va в правой части (18) при х=х_ должен соответствовать МЗК, падающим слева. На правой границе х+ следует положить а=0.
При обратной прогонке для интегрирования (18) от точки Xs к х_ и Х+ необходимо задать начальное условие для т в точке Xs. Оно находится из требования непрерывности функций Т(х) и Т'{х) в точке Xs: t'(xs) =
=K~lA (xs—0)т (x3) +K~la(xs—0) —К~ХА (о^-ЬО) т (xs), откуда Т(ха) = (Л (ха+0)— A (xs—0))~la{xs—0).
Фиктивные особые точки, в которых D=0, оказалось удобным обходить в комплексной плоскости. При этом не нарушалась устойчивость интегрирования и сохранялась точность результатов.
Коэффициенты отражения МЗК и трансформации в ЭК определялись по х-компонентам вектора Пойнтинга. В области применимости квазиклас - сического приближения для этих величин использовались выражения
МЗК------ 1 (8~ДГ» > дг |Д| » 5 эк------------- C_t(e-Np
8я D 1 1 ’ 8я N. Y 1 1
На рис. 2, 3 показаны результаты численного счета и расчета по формулам (4), (12), (13), (14). Отметим отсутствие симметрии рис. 2 относительно изменения знака Ny.
Для того чтобы повысить точность последних формул, величины Г, Ф при NvҐ[87]0, G^O брались не из приближенных аналитических выражений (13), (14), а рассчитывались численно по формулам
Xi
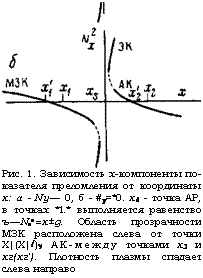
Рис. 2. Линии уровня коэффициента трансформации МЗК в ЭК на плоскости параметров х=Л^/| е*' | 1/1, —g| | ех'|%. Кривые отвечают значениям коэффициента трансформации: ^ - 10“в; 2-10-5; 3 — 10“4; 4- - Ю“3; 5-10-3; 6- 210“2; 7-0,2; 5-0,5; % 9 - 0,8; .Ю — 1. На жирных линиях т обращается в нуль
|
|
|
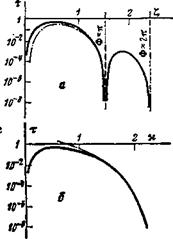
Рис. 3. Характерные зависимости коэффициента трансформации от параметров задачи: а-зависимость от £ при #„=0 (штрихпунктир - расчет по (4)) ; Б - зависимость от х при £=0 (штрихпунктир - расчет по (12)); « — зависимость от £ при х/£*1,26 (сечение рис. 2 по лучу 0Р, в точке Р величина т=1); штрихпунктир - расчет по (4) |
 От Ха. Добротность такого резонатора определяется коэффициентом трансформации МЗК. Поэтому в основе численных расчетов добротности плазменного шнура [14] или импеданса антенны, возбуждающей МЗК [8, 15], неявно лежит определение коэффициента трансформации. Нетрудно показать, что добротность плазменного шнура по порядку величины равна (1(оР{/с) (ю/ю<) (1/т).
От Ха. Добротность такого резонатора определяется коэффициентом трансформации МЗК. Поэтому в основе численных расчетов добротности плазменного шнура [14] или импеданса антенны, возбуждающей МЗК [8, 15], неявно лежит определение коэффициента трансформации. Нетрудно показать, что добротность плазменного шнура по порядку величины равна (1(оР{/с) (ю/ю<) (1/т).
За обсуждение работы авторы благодарны А. В. Звонкову.
ПРИЛОЖЕНИЕ
Полная система коэффициентов отражения и трансформации. В настоящем Приложении в соответствии со сказанным в конце раздела 2в при расчетах р, т не учитывается отражение АК от правой границы области непрозрачности - точки х2(х»'). Для того чтобы рассчитать полную систему коэффициентов отражения и трансформации, обратимся к исходной системе (1). Вдали от точки АР она распадается на два независимых уравнения (2), (3). В ее окрестности система (1) может быть сведена к одному уравнению четвертого порядка
1
—ф'/йч&ф"+ф-о,
Л
Где
<р-|в<Ьг, Л-|е,|е.'*/ЛГ, У»1.
Данное уравнение исследовано достаточно подробно [16, 17]. Результаты этих работ использовались при построении решений в окрестности точки АР, в остальной области анализ производплся так же, как и в разд. 2. В результате были найдены коэффициенты отражения — /?, и трансформации — 7* (индекс «1» резервируется для МЗК, «2» — для АК, «3» — для ЭК) :
Д1==1_е-*г + 0(<?-*г), Я2~Дз=0(е-2Г),
Гн-Г«—в-*,+0(е-зг)| 7’1а=»7’л=»в“г+0(в~зг), Г„-Гп - -1 - _1 в-*г+о(#-*г).
В случае слабого затухания АК найденные коэффициенты позволяют независимым способом рассчитать величины р, т, определенные в основном тексте. При этом амплитуда А стоячих АК определяется из условия согласования АК, падающих на точку АР, и уходящих от этой точки. Например, в случае N„=0 оно имеет вид
Л=-(Л/?^Г|2)ехр(21ф).
Коэффициенты р, т (см. разд. 2) даются выражениями р= (Ri+ATu)z, т=(7*1з+.А2э1)*. Нетрудно найти, что данные выражения совпадают с найденными в разд. 2а.
Отметим также, что в [3, 4] для нахождения полной системы коэффициентов отражения и трансформации использовалось модельное уравнение туннелирования, к которому применим метод интегрального преобразования Лапласа. С относительной точностью 0(е~2Г) полученные в этих работах коэффициенты совпадают с найденными здесь.