ФИЗИКА ПЛАЗМЫ

ТЕОРИЯ ЦИКЛОТРОННОГО НАГРЕВА В ДЛИННЫХ АДИАБАТИЧЕСКИХ ЛОВУШКАХ

А. В. ТИМОФЕЕВ Введение

Для нагрева плазмы в адиабатических ловушках часто используются циклотронные колебания. Колебания могут обмениваться энергией с заря­женными частицами, если частота колебаний о совпадает с циклотронной (О) (/—е, 0 - Магнитное поле адиабатических ловушек нарастает от центра к торцам системы, поэтому резонансное условие может быть удовлетворе­но лишь в отдельных точках: одной при ©=(»)*>, двух при а>>со^. Здесь (о# — минимальное значение циклотронной частоты в ловушке.'

Заряженные частицы при своем движении между магнитными пробка­ми (областями большего магнитного поля) периодически проходят через резонансные точки. Результат каждого отдельного акта резонансного взаи­модействия зависит от соотношения между фазой электромагнитных коле­баний и фазой циклотронного вращения частицы в момент прохождения через резонанс. Возникает вопрос — можно ли при описании этого процес­са использовать приближение хаотических фаз? Положительный ответ не­избежно повлек бы за собой вывод о диффузии функции распределения по шкале энергии, т. е. о нагреве плазмы.

Эволюция фазы при циклотронном взаимодействии была впервые про­слежена в работе [4]. В этой работе показано, что хотя энергия частиц под действием циклотронных колебаний меняется во времени, однако эти из­менения оказываются периодическими, а движение частиц по фазовой плоскости характеризуется новым адиабатическим' инвариантом, заменяю­щим магнитный момент. Этот результат был получен для коротких лову­шек, в которых за одно прохождение между пробками частица не успевает выйти из резонанса. с колебаниями. Ловушку можно считать короткой, если ее длина Ьь не превышает (Ьг^ здесь Ь — характерный масштаб измене­ния магнитного поля, ri — ларморовский радиус заряженных частиц *.

Однако согласно общей теории возникновендя стохастичности в дина­мических системах адиабатические инварианты могут быть разрушены при «перекрытии резонансов» в фазовом пространстве (см., например, [2-3]). К проблеме циклотронного нагрева эта теория была применена в работах [4- *]. В [5], как и в [*], рассматривались короткие ловушки, в [4] — длинные. Было показано, что явление «перекрытия резонансов», приводящее к нагреву плазмы, наступает при достаточно большой ампли­туде электрического поля циклотронных колебаний. Условия* «перекры­тия», полученные в этих работах, можно представить в виде

ПРИ

Е>н°т (£) (■?) пр

Во всех этих работах рассматривалась идеализированная проблема без учета случайных воздействий на движение частиц[36]. Между тем в реаль­ной плазме скорость частиц должна хаотически меняться под действием кулоновских соударений, а из-за неизбежной немонохроматичности цикло­тронных колебаний фаза последних не может считаться вполне регуляр­ной.

Действительно, за одно колебание между пробками заряженная части­ца успеет совершить N « — > 1 оборотов по циклотронной окружности.

Случайные воздействия не «собьют» фазу лишь в том случае, если за это время скорость частицы изменится на бу<у/Л^, а ширина спектра цикло­тронных колебаний б© не превышает ©/ТУ. Например, при Г#=102 эв, Я0= «Ю3 гс, Ь=10г см величина Л^Ю4, и, следовательно, плотность плазмы не должна превышать 1010 слс~3, а ширина спектра 10~г о)в.

Отметим также, что в указанных выше работах рассматривалась неса - мосогласованная задача, а именно, анализировалось движение заряжен­ных частиц в поле заданной волны. Обратное влияние плазмы на колеба­ния не учитывалось. Наконец, из-за математических трудностей до сих пор остался невыясненным характер движения частиц в длинных ловушках при малой амплитуде волны.

В настоящей работе рассматривается проблема циклотронного нагрева плазмы в длинных ловушках (Ь0> (Ьг^4*). В разделе 1 случайный элемент исключен из проблемы. Показано, что движению ансамбля частиц под дей­ствием циклотронных колебаний соответствует преобразование фазовой плоскости (энергия — фазовый угол), сохраняющее площадь и состоящее из поворотов вокруг начала координат и сдвигов. При этом энергия от­дельной частицы меняется во времени периодически, и, следовательно, циклотронные колебания не нагревают плазму. Этот результат справедлив,

Если амплитуда колебаний достаточно мала Е<.Н0~ (“£“) ("]£’)

В обратном случае, в соответствии с [*■3], «резонансы перекрываются» и движение становится стохастическим (см. также [*]). Теория перекрытия резонансов в значительной мере эвристична. Проблема циклотронного на­грева предлагает сравнительно простую геометрическую модель (преобра­зование, состоящее из поворотов и сдвигов), на которой эта теория могла бы иметь дополнительную проверку.

В двух последующих разделах исследуется влияние случайных воздей­ствий на процесс резонансного циклотронного взаимодействия. В разде­ле 2 интенсивность случайных воздействий предполагается настолько большой, что траектория частицы на фазовой плоскости напоминает тра­екторию броуновской частицы. В разделе 3 рассматриваются случайные воздействия малой интенсивности, которые оказывают слабое влияние на движение частиц по фазовой плоскости. Найдено, что в обоих случаях за­ряженные частицы набирают энергию в поле циклотронных колебаний, причем с усилением интенсивности случайных воздействии скорость нагре­ва плазмы возрастает. Предельное значение скорости нагрева получается в приближении хаотических фаз, когда считается, что фаза «сбивается» при каждом прохождении через резонанс.

Задача о резонансном взаимодействии циклотронных колебаний с за­ряженными частицами, удерживаемыми в магнитной ловушке, в некоторых отношениях близка к задаче о резонансном взаимодействии заряженных частиц с волной конечной амплитуды (см., например, [7]). В частности, и в нашем случае можно использовать понятия: пролетные и захваченные частицы. При этом явление захвата состоит в том, что циклотронная вол­на навязывает частице определенное значение частоты колебаний между магнитными пробками. В то же время специфика задачи о циклотронном: взаимодействии позволяет использовать более простые и эффективные ме­тоды. А именно, при наличии случайных воздействий эволюция функции распределения частиц под действием циклотронных колебаний может быть описана с помощью уравнения Фоккера — Планка, в котором независи­мыми переменными являются лишь время и энергия. С помощью этого уравнения мы получили простые выражения для количества энергии, по­глощаемой плазмой, и показали, что окрестность сепаратрисы, разделяю­щей области пролетных и захваченных траекторий, дает малый вклад в конечный результат. Напомним, что в задаче о движении частиц в поле волны конечной амплитуды аккуратный учет кулоновских соударений на движение частиц в окрестности сепаратрисы представляет значительные трудности.

В последнем 4 разделе настоящей работы рассматривается самосогла­сованная задача о распространении циклотронных колебаний по плазме,, удерживаемой в магнитной ловушке. Такое рассмотрение удается провес­ти при со>(»)*>, когда имеются две резонансные точки, симметрично распо­ложенные относительно минимума магнитного поля, причем области ре^ зонансаого взаимодействия, окружающие каждую из резонансных точек, не перекрываются.

В этом случае в окрестности резонансных точек зависимость магнитно­го поля от координаты может быть аппроксимирована линейной функцией, а волновое уравнение сводится к уравнению Уиттекера, решения которо­го хорошо изучены. Волновое уравнение имеет особенность в точке цикло­тронного резонанса, где осуществляется обмен энергией между плазмой и циклотронными колебаниями. Поэтому оказывается, что вся динамика ре­зонансного взаимодействия может быть эффективно учтена в правиле про­должения решения через резонансную точку. Интересно, что правилу об­хода Ландау соответствует приближение хаотических фаз при описании резонансного взаимодействия. Этот результат фактически содержится в ра­боте [8]. Методом, который ранее использовался в этой работе, мы нашли правила продолжения решений при произвольной интенсивности случай­ных воздействий. С их помощью решено волновое уравнение й получены значения коэффициентов отражения, поглощения и прохождения цикло­тронных колебаний, падающих на адиабатическую ловушку.

1. Проблема нагрева при отсутствии случайных воздействий

А) Модель с «дискретным» временем.

Рассмотрим электромагнитные колебания с круговой поляризацией, электрический вектор которых вращается в ту же сторону, что и электро­ны в магнитном поле. Уравнение движения отдельного электрона предста­вим в виде

Здесь v-=vx—ivv, ось OZ направлена вдоль магнитного поля. В (1) опу­щено слагаемое, учитывающее изменение скорости ларморовского враще­ния под действием магнитного поля колебаний. Оно мало, если выполняет­ся условие < 1, где к— волновой вектор колебаний. Для ОПреДелеН-

UJ.

Ности рассматриваем нагрев электронной компоненты плазмы.

Примем, что постоянное магнитное поле меняется по простейшему за­кону, обеспечивающему конфигурацию магнитной ловушки H(z) =Я0(1+

-f-z2/L2). В таком поле траектория электрона дается выражением

Z(t)=L—-sin(о)б(t £0));

V±0

Здесь Уцо(у-1-о) —скорость движения электрона в. направлении вдоль (попе­рек) магнитного поля в точке z=0, ауь=и±0/Ь — частота колебаний между пробками магнитной ловушки.

Однородное уравнение, соответствующее (1), описывает свободное вра-

1

Щение электрона по ларморовской окружности (t) *=*v± exp i J dt'm* (tf) j.

Решение полного уравнения (1) показывает, что в результате прохож­дения через резонансную точку z,=z(tt) амплитуда и фаза циклотронного вращения меняются

ЕЕ

--------- (2)

Те

Здесь t — интервал времени, в течение которого заряженная частица на-

Ts

Ходится в резонансной зоне, a(f.) = ^ dt'((щe(t') — ю)4-Да. При резонансе

В МИНИМуМе МаГНИТНОГО ПОЛЯ (более ТОЧНО При Ьд|<^ЛУ..о 0)Го ')

Af=3v*r (£/1>„о)'лсо;о Да=0.

Если резонансная точка сдвинута к краю системы:

И.^^’УцошГо'- то At= /Vh(z)^-J, Да=я/4.

При zs=0 вычисления оказываются более простыми. Этот случай мы и рас­смотрим вначале.

Уравнение (2), разумеется, содержит лишь часть информации о воз­действии электромагнитных колебаний на частицы. Однако этой информа­ции достаточно для того, чтобы учесть кумулятивные эффекты, накапли­вающиеся за много актов резонансного взаимодействия. Такой способ приближенного описания процесса резонансного взаимодействия принято называть импульсным приближением (см., например, [* *]).

Импульсное приближение позволяет проследить за движением частиц на фазовой плоскости, рассматривая значения величин v±, а в дискретные моменты времени, разделенные промежутками, равными я/юь. Поэтому использование импульсного приближения эквивалентно введению дискрет­ного времени.

Из (2) следует, что за одно прохождение через резонанс, т. е. за поло­вину периода колебаний частицы между пробками магнитной ловушки,

Модуль скорости и фазовый угол меняются следующим образом:

TOC o "1-5" h z 1>х, п+1=^х, 2Дух, „ cos а„+Д (3)

1 - _|_ . / у-ь»+А 1 _ ...

Ocn+i = —-a„+arctg (

2 v±, А 2 /

Здесь введен дискретный аргумент п — число прохождений через резо­нанс. Величины v±, п, ап берутся в момент времени, непосредственна сле­дующий за актом резонансного взаимодействия, «),

£2(*>х,») = — ые 0LvnozvZ3n, набег Фазы а(t)=Јdt'(<j3e(t')—<a) вычисли-

2 ’ ^

ется за половину периода колебаний электрона между пробками, электри­ческое поле считается достаточно слабым, так что выполняется условие

А = — EAt<^v±. те

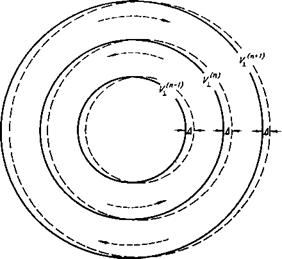
В соответствии с (3), (4) переход от v L>n, ап к v±t n+1, an+i происходит в два этапа. На первом меняется лишь фаза ап-^ап - Это преобразование описывает движение частицы между последовательными прохождениями через резонанс. Ему соответствует вращение плоскости и±, а на рис. 1. Весьма существенно, что угол поворота зависит от скорости v±. На втором этапе вся картина, как целое, сдвигается вдоль электрического поля на величину А. (Ввиду того что фаза циклотронного вращения отсчитывает­ся от фазы волны, мы фактически работаем во вращающейся системе ко­ординат, где электрическое поле постоянно во времени.) Фазовая площадь сохраняется на обоих этапах. Этот результат вполне естествен, так как мы рассматриваем консервативную динамическую систему. Чтобы плазма на­гревалась, в движении частиц должна появиться тенденция к увеличению y_L, т. е. оно должно стать необратимым. На первый взгляд, такая тенден­ция в движении частиц действительно имеется (см. последнее слагаемое и (3)). Однако, например, в интересующем нас случае слабого электриче -

А,

Ского поля это слагаемое имеет второй порядок малости по — < 1? и в

V±

Выражении для v±, найденном из (3), (4), оно компенсируется другими слагаемыми, имеющими тот же порядок величины (см. ниже).

Прежде чем решать уравнения (3), (4), полезно представить себе об­щий характер движения частиц на фазовой плоскости и±, а. Частицы, ко­торые в течение сравнительно долгого времени приходят в резонансную точку при одном и том же значении фазы а, естественно назвать резонанс­ными. При — «с 1 условие резонанса имеет вид Q(F(±))=2кт.

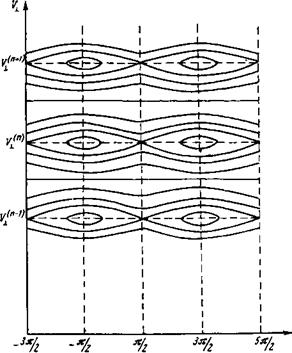
Вблизи линии v±s=V(±) находятся неподвижные точки фазового про­странства, для них a«ji(Z+V2) (см. рис. 2). Как обычно, в задачах о резо­нансном взаимодействии устойчивые (эллиптические) точки равновесия чередуются с неустойчивыми (гиперболическими). Эллиптические точки окружены траекториями частиц, «захваченных» волной. Эти частицы впол­не заслуживают свое название, так как их фаза испытывает лишь неболь­шие колебания относительно фазы волны. (Напомним, что мы работаем в системе координат, вращающейся вместе с полем волны.) Ширина области, занятой захваченными траекториями, по порядку величины равна

G разделе 16) (см. ниже) уравнения, описывающие движе -

K A dvj

Ние в области приведены к стандартному виду. Вдали от липни

^1= V*™* располагаются траектории пролетных частиц. На этих траекто­риях фаза испытывает систематическое приращение. Если

1

(1£2-^

То траектории пролетных частиц слабо отличаются от пря -

Мых линии, и поэтому при их анализе можно использовать метод последо­вательных приближений. Введем новую переменную г^п=^1,пи предста­вим уравнения движения в виде ряда по малому отношению Уравнение (3) уже имеет требуемый вид, а вместо (4) получаем

А»+і=аЛ+А/и)п біп ап+А2'/2шп віп 2ап.

Решая систему (3), (5) методом последовательных приближений, иа -

10ДИМ

(0)

IV п =г^о,

Ап(0)=а0+Агй(0),

Шп(1)=Ашо бш-1 ) [ —^ (а° "^_2_^(°)) (а«0> "^~2^^(0) )] ’

АЛ(1)=—біп-2 (—£2{0) ) [—сое ао+соя ] +

2 аьио 2 /

+ -^-и;о ^эш-1 ) ^—соз^ао + —й(0) ^+соз ^ап0) + —^(0) | ,

WГ = - у sin-2 ( - у й<0>) [ і-cos («О“') ] -

-^Ш^8ІП'3 (тй<0)) [cos (тй'°’) +cos (2a)+TQW)"

—cos + j&(0) cos^a0+ai0) + —Q(0) cos(2ao+ЗQ^0)) +

TOC o "1-5" h z -^-cos(2aГ>) +Q(0)) ] . (10)

Здесь w0, ae — начальные значения w, a;

Q{0)=Q(w0)—— sin-1 (— Q(h70) sin (a0 + 4-&(и>о) .

2 dwо 2 / 2 /

При вычислениях использована формула

П—1 X X 1

^cos(Лж+у)- — 8ІП-* (-у) [ sin +sin (( п —2 ) Я+У)]

О

(см., например, {10]).

Мы нашли, что в области w—W{m)^>v/U [——— траектории про-

Д Dw1

Летных частиц слабо отличаются от прямых iz;=const; здесь Wlm)*= = (^?))2 — такие траектории представляют непроницаемые барьеры для захваченных частиц, чьи траектории расположены в области w^W{m). Поэтому и у последних величина w может измениться лишь в ограничен­ных пределах. Отсюда следует, что электромагнитные колебания не могут нагреть плазму. Наше рассмотрение относится к колебаниям малой ампли-

DQ

Туды, когда выполняется условие д--- <1, и поэтому траектории основ-

Dv ±

Ной массы пролетных частиц близки к прямым линиям. При решении си­стемы (3),' (4) мы учли лишь члены второго порвдка малости по Д/и/7’. Вообще говоря, нельзя исключить возможность того, что в высших поряд­ках по этому параметру траектории (6) — (10) окажутся неустойчивыми. Сходные вопросы, как известно, встают в проблеме устойчивости планет­ных орбит и т. д. (см., например, [2-3]). К настоящему времени по этому вопросу общепринята следующая точка зрения. Траектории становятся не­устойчивыми, если происходит явление «перекрытия резонансов», т. е. ширина области «захватываемой» т-м резонансом превышает расстояние между этим резонансом и соседними. В интересующей нас йроблеме усло-

DQ j-j

Вие перекрытия имеет вид Д---- > 1. Ыри выполнении этого условия дви-

Dv±

Жение частиц по фазовой плоскости приобретает характер беспорядочного блуждания. Вспоминая определения Q и Д, нетрудно сообразить, что час­тица переходит от одного резонанса к другому за один акт взаимодействия с циклотронными колебаниями, и, следовательно, за это же время исчеза­ет фазовая корреляция. Таким образом, мы приходим к заключению, что

Если Л------ > 1, то при описании взаимодеиствия частиц с циклотронны-

(1и±

Ми колебаниями мы можем использовать приближение хаотических фаз. Нетрудно видеть, что условие перекрытия резонансов совпадает с полу­ченный в [4] (см. также введение).,

.Сопоставим теперь наши результаты с результатами, полученными в Iе*11 ]. В э’Гих работах уравнения, аналогичные (3), (4), интегрировались на электронно-счетной машине. Было найдено, что малая доля частиц на­долго задерживается в окрестности неподвижных точек фазового простран­ства, а остальные ускоряются электрическим полем волны до произвольно больших значений энергии. Эти результаты свидетельствуют о необрати­мом характере движения частиц на плоскости и;, а и несохранении фазо­вой площади. Возможно, что они являются следствием приближений, сде­ланных при численных расчетах. Действительно, в [*•11 ] фазовая плос­кость была разделена на ячейки конечного размера, и анализировалось движение частиц по этим ячейкам. При таком описании неизбежна потеря некоторой части информации, а следовательно, должен вноситься и эле­мент необратимости. По существу именно таким образом происходит пе­реход от обратимого уравнения Лиувилля к необратимым кинетическому уравнению и уравнениям гидродинамики. Б статистической механике ис­пользование величин, усредненных по конечным ячейкам фазового про­странства, называется введением крупнозернистого распределения (см., например, [**■|3]). Такая интерпретация результатов, полученных в [•■11 ], подтверждается рассмотрением, проведенным в последующих разделах настоящей работы. Нами показано, что если частицы подвергнуть случай -

Яым воздействиям, то они действительно начинают набирать энергию в поле электромагнитных колебаний, причем скорость нагрева плазмы воз* растает с увеличением интенсивности случайных воздействий.

Б) Модель с непрерывным временем

Для дальнейшего полезно более подробно рассмотреть движение час­тиц в резонансной области w=Wlm). Используем то обстоятельство, что в этой области Q«2пт. Введем безразмерные величины б=Д/м;ав, U—w/wat где ivа — некоторое характерное, например среднее значение w. Если

TOC o "1-5" h z Шы) =Q—2nm-+0, 6-^0,

До отношение бЙ(я0/б остается конечной величиной, то можно ввести не­прерывное безразмерное «время» т]=п6. Чтобы найти производные

1У = -1_ а = , представим уравнения (3), (5) в виде

Dx dx

Ип„-ь=опь+-^ипьг+..., (ID

I

Ая+,—an=dn6 + — an62+..., (12)

где tfn, a«, а« являются функциями Un, ап. В (11), (12) введены члены со вторыми производными tfn, «п, пропорциональные б2, которым в урав­нениях (3), (5) соответствуют слагаемые, пропорциональные Д2. Это сде­лано с единственной целью показать, что и в модели с непрерывным вре­менем отсутствует эффект непрерывного увеличения энергии, к которому на первый взгляд должны приводить эти слагаемые. При конкретных рас­четах они в сцлу своей малости не будут учитываться.

TOC o "1-5" h z Д д

Используя равенства tfn=Cn------ tfn+du---- Cnt

DUn дап

An=ftn - Г77- ctn+ctn - т— tin,

DUn da« tr-2irh cos oc-6Q{m)U4' sin a, (14)

A=CD(m) (U)—U~4t sin a —T77W* 6Q(m))cos a. (14)

du

Здесь cd(wi>(^) =BS6Q(m)/6. Уравнения (13), (14) могут быть получены из гамильтониана:

И

H{U, a)= J dU' a>lm) (V) —2U% sin a—If' 6Й1"’ cos a. (15)

Из (13) — (15) следует, что слагаемые, пропорциональные (6Q(m)), кото­рые своим появлением обязаны учету вторых производных в (11), (12), лишь слегка искажают траектории-частиц на фазовой плоскости, не меняя пх общего вида. При 6Q(m)<l эти слагаемые могут быть опущены.

TOC o "1-5" h z / 1 d Ч*

Перейдем к новым переменным Ца (U—U(m)) (U(m)) ~'и I-------------- — G)(m) ) ,

2 dU /

т=т](Uim))'u (2-^-©(m)) и сместим угол а на —я/2. Здесь U(m)=Wlm)/wa. dU I

Тогда гамильтониан (15) принимает стандартный вид

1

Н(и, а) = — и2—cos а. (16)

Движение, описываемое гамильтонианом (16), происходит по траекто­риям

“-Mr к(т)Ь от

А=Во+м(/)т. (19)

4& / 1 кл / 1

Здесь / =------- Е(—), «(/) =------- (—), Е и К — полные эллипти-

Л к / К к /

Ческие интегралы, к=(1/г+Н/2)ъ (см., например, [*■10]).

Приведем также разложение Фурье «скорости» и по 0:

И=А:лК"1 ^1+4 ^ qn (l+qtn) cos п0 ^. (20)

»—1

Здесь 9=ехр ( - л/2 К' К-’ (-Ц-)) .

Выражения (17) — (20) описывают движение пролетных частиц. Ана­логичные выражения можно было бы привести и для захваченных частиц, однако ниже мы увидим, что захваченные частицы играют весьма малую роль в интересующих нас процессах.

2. Нагрев при наличии интенсивных случайных воздействий

А) Движение отдельных частиц

Предположим теперь, что система, рассматриваемая нами, подвержена случайным воздействиям. Под их влиянием фаза ая. за время между по­следовательными прохождениями через резонанс (половину периода коле­баний по ловушке) испытывает случайные приращения соп. Примем, что величины cd„ подчиняются нормальному закону

/(соп) = (2я)”1/,о”1 ехр(—соя2/2а2) (21)

И б — коррелированы по индексу п (дискретному времени). Будем счи­тать, что случайные воздействия нарушают фазовую корреляцию прежде, чем волна успеет «захватить» частицы. Таким будет характер движения

DQ

Частиц, если а[37]>Дш7*--- . Фактически это условие означает, что за харак-

Dw

Терное время корреляции Q(u>) меняется на малую величину. В этом слу­чае на всей фазовой плоскости траектории частиц могут быть найдены методом последовательных приближений по параметру Дlwh (см. раздел 1а)). По аналогии с (6) — (10) получаем

П

TOC o "1-5" h z ая(0) =a0+7iQ0+ (23)

Ктт 1

Я

U'»1 -*2Д ш»'* у1,cos (а»"’), (24)

А„(1>=—Дш» А У, sin(аГ*) +2ДУ*, У, соз(а,(0)), (25)

У0Л

Кшт 1 ft—■ 1 /»1

Ш‘г> =2Дг£ 2 cos (оС-а,“”) +Д*(га+1) - к«1 і —1

-2Дгш„ Vі V' V (sin (аі,*і,-а» ’ ) +sin (<&!,.»+<**’ )). (26)

m—1 і —1 ft—l

Подставим в (26) выражение для ai (23) и усредним по статистическому ансамблю (начальной фазе и распределению (21)). При вычислениях используем формулы

»

^соз (а+ У, ш> )^=cosaP’,~m+1, (27)

Кт*ГП

Г.—1

У1 Р* cos (кх+у) =* (cos у—cos (х—у) — $п cos (пх+у) +

ЛшшшЛ----------------------------------------------

Ft—о

+Ря+1соз((л—1)х+у)) (1—2(i cosx+jj2)-1. (28)

Здесь скобки означают усреднение по статистическому ансамблю, 0=

Оо

= ^ <*(•>*/(<«>*) cosG)neexp(—о72) —формула суммирования (28) взята из

—оо

[10]. При р*=0 она переходит в формулу, использовавшуюся в разделе 1а) (см. (6)-(Ю)).

Вычисления приводят к следующему результату:

<ц>.>=ш,+пД,-^-1Р.- 1 Р (29)

Dw0 l,-f-[J—2$ cos Й(ш0)

Это выражение показывает, что при наличии случайных воздействий частицы могут как увеличивать, так и уменьшать свою энергию. Соответ­ствующие области значений w чередуются с периодом 2л (-^) <w.

Dw /.

С уменьшением р области значений ш, в которых энергия уменьшается, сокращаются. В предельном случае р=*0 все частицы поглощают энергию колебаний, и (29) переходит в выражение, полученное в [4], в приближе­нии хаотических фаз.

Покажем теперь, что аналогичные результаты получаются и в модели с непрерывным временем. Опустим в (13), (14) малые слагаемые, пропор­циональные 6Q(m), и введем в (14) случайную величину <о(т|), б-корреля - рованную во времени <o)(t|)(i)(ii/)>=oV6 б(ц—т|') и распределенную по нормальному закону. В результате вместо (13), (14) получаем

TOC o "1-5" h z C=2lfh cos а, (30)

A=cD(m) (U)-U-'k sin а+ю (г). (31)

Решая (30), (31), приходим к выражениям, которые отличаются от (22)—

(25) заменой сумм на интегралы по/времени. Выражение, аналогичное

(26) , удобно представить в виде

DUw

—------ =21 cos (a(0) (л) - a(0) (V)) “

®Л i

D(D(m) 'ГГ

-W—Г8йи(«‘*»(я)) *l" cos(a(e'(n")). (32)

0 0

Это выражение следует усреднить по статистическому ансамблю. Покажем, как это делается на примере экспоненты ехр(их(0>(11)"”*а<0>(л/))- В выра­жении для а(0) (т|) —сс(0) (“П7) перейдем от интегрирования к суммированию

Ц/Ь

TOC O "1-5" H Z Се"» (п) - а"» (л') = (n-n ) ®<т)+6 2, <■>*• (33)

Л-ч'/а

Используя независимость а* при б-*-0, и учитывая (21), находим

<ехр(ia(0) (ц) —ia(0) (tj') ) >=ехр(i(tj—tjO o(m)) (<ехр(icd6) >)п~ч'/#=

•=аехр(т]—т)7) (id>(w,)—aV26). (34)

Нетрудно заметить, что вычисление (34) аналогично вычислению интегра­ла по случайным траекториям, введенного Винером (см., например, [4*1). Вычисляя (32) с помощью (34), получаем

Dw л. d о*

— )б*Л2 — w--------- —-------------- . (35)

Di / dw /a* * , /вл, чч„

1 (у) +№{т)У

Здесь использованы соотношения т]=лб, o)(m)=6Q(m)6“1, 6Q<m)=Q—

—2лт.

Исходные уравнения (30)^ (31) имеют смысл лишь при бй(,и)“»-0, а2-^0. В этом случае cos (6Q(m))«l— ~(6Q(m))2, P=<cos ^ 1—^0*,

И (29) переходит в (35).

Б) Эволюция функции распределения

На интервалах времени, существенно превышающих характерное вре­мя фазовых корреляций, эволюция функции распределения

F(w) может быть изучена с помощью уравнения Фоккера — Планка (см., например, [14]). В это уравнение в качестве коэффициентов входят сила динамического трения и коэффициент диффузии. Первая из этих величин была определена в предыдущем разделе. Для вычисления коэффициента

Диффузии достаточно знать Шп* (см., например, [14]). Используя (24), находим

D(w) = 4-<((ц>.+1-ц^.)г-(ц>п-ц>.))>°Дгш. 1 ^ . (36)

2 1+[г--2рсо8&(ш)

»-►оо

Поскольку оказалось, что сила динамического трения ^ и коэф­

Фициент диффузии удовлетворяют соотношению /-^1б = -^-/>(и?),

Д,\ /

То уравнение Фоккера — Планка принимает следующий вид:

1 а/ Д а/

2а>ь dt dw dw

Здесь учтено, что акты резонансного взаимодействия разделены интер­валом времени (Зсйб)-1, ©6 —частота колебаний электрона по ловушке, Q (/, t, w) — плотность источников и стоков частиц.

В настоящей работе рассматриваются длинные ловушки, для которых

Выполняется условие Й=^£о)ео1>||о21>_|_о"а>1. Если разброс в распределении

По поперечным скоростям не слишком мал, то распределение по попереч­ным скоростям захватывает большое число резонансов Q(W(M))=2nm. Коэффициент диффузии колеблется при изменении w, принимая макси­мальные значения npir w*=W(m). Разумно использовать усредненный коэф­фициент диффузии Dav. Определим его таким образом, чтобы поток частиц

TOC o "1-5" h z по оси w, вычисленный с помощью усредненных величин Dav{w), ,

Равнялся истинному

/---- Dn-^-=-D~. (38)

OW Ow

Функция D(w) включает в себя «быструю» зависимость, входящую через cos{Q(h>)) и «медленную» (см. (36)). Наша цель состоит в устранении «быстрой» зависимости. Функция cos (Q (ш)) близка к периодической, и нам достаточно усреднить D(w) по одному «периоду», т. е. по интервалу

W+ где • Медленная зависимость от w будет

( DQ “х

Учитываться параметрически. Поскольку на интервалах порядка 2л I )

Усредненная функция распределения меняется на весьма малую величину, то производная может быть заменена на (Ж(+т) — W^)”1 (/(1У+|)) — —/(Wl"^)). С другой стороны, из (38) следует / (Wjn>) _ / (Wlm)) = -

*£•>

. Сопоставляя эти выражения, получаем

W(m>

D.W = <"Г - И*"’) - AVT+f • <39)

Заметим, что прямое усреднение (34) дало бы результат, не зависящий от р, Д„,=Д2ш, что совпадает с истинным коэффициентом диффузии при Р=0, т. е. в приближении хаотических фаз. Коэффициент диффузии £)=Д2ш следует использовать в момент включения циклотронных колеба­ний, пока распределение еще не промодулировано волной. Однако срав­нительно быстро частицы перераспределяются таким образом, что их кон­центрация повышается в области, где коэффициент диффузии мал, и по­нижается там, где он велик. Естественно, что при этом среднее значение коэффициента диффузии уменьшается (см. (39)).

TOC o "1-5" h z С помощью (39) находим среднюю скорость прироста т. е.

Силу динамического трения

1 / (1ш д, 1—В2

----- (----- ) =--------- Д«„=Да—(40)

2а>Д dt / «„ <1и> 1+р2

Из (40) следует, что при усилении интенсивности случайных воздействий, т. е. при р-^0, скорость нагрева плазмы возрастает. В предельном случае •Р=0, когда при рассмотрении процесса можно использовать приближение хаотических фаз, приходим к выражению, использовавшемуся в [4]. Следует отметить, что для распределений с малым разбросом

„

(----- ) нельзя использовать усредненные величины. В этом случае

(1и? }

Скорость нагрева йш/(И (см. (29)) может существенно отличаться от (40).

Более того, если частицы сконцентрированы в области, где ------- < 0, то

Йш

Они будут отдавать свою энергию колебаниям, т. е. плазма окажется не­устойчивой.

3. Нагрев при слабых случайных воздействиях

Если фазовая корреляция сохраняется в течение длительного времени / dQ - Ч*

(---- ) , то случайные воздействия слабо влияют на

DwJ

Движение частиц по фазовой плоскости, и это влияние может быть учте­но по методу последовательных приближений. Вдали от резонансной зоны

^ ш—И7(т)>Д,/,ш'/4^-^г^ | , т. е. в области, где траектории близки к

Прямым линиям, мы можем использовать результаты предыдущего разде­ла. Однако окрестность прямой ш—И74”0 требует специального рассмотре­ния. Чтобы учесть случайные воздействия, дополним гамильтониан (16) слагаемым ц©(т).

В = и2—соз а+в® (т). (41)

Здесь в соответствии с (31) случайная функция Э(т) определена как

D<й{n)-'l^

Л©* ' Л

2~ш~) *

Из (41) для иу а можно получить уравнения, аналогичные (30), (31). Однако вместо щ а целесообразно использовать переменные действия /, 0, введенные в разделе 16. Уравнения для поправок /(1), 0(1), обязанных случайным воздействиям, имеют вид

Ди

TOC O "1-5" H Z /(1,=-(0( т)-—, (42)

О и

ЙшЦ) ди

0(1) =—77—/(1,+ю(т)-^-. (43)

АI о1

Из (42), (43) следует

* о тт

Йт'ы(т')—(/,0(т')), (44)

Е<‘'=рт'а(т')~(/,0(тО)--^^|йт'|йт''а)(т")~£/(/,0(т")),

(45)

С помощью (44) находим выражение для коэффициента диффузии

В2 / / ди 2

(46)

С1(0^т^ ~^2

2 ) <1, гг (0) определяется (20), скобки

(Ш /

Со значком 0 означают усреднение по начальной фазе.

Чтобы найти коэффициент динамического трения, представим гамиль­тониан Й в виде й=Й+и& (т), где Н — невозмущенный гамильтониан (16). Поскольку (1Й/йх=и((1(о/(1х), то для (1Н/с1т получаем

/(1)——^(46) и используя при вы­числении (|б5(т)-^) (44), (45) , находим

/ й1{2) ба / / ди д2и ди д2и

”^Г/ Т дд ддд1~ д! до* / / 0е (48)

Если в этом выражении проинтегрировать по частям, то нетрудно найти,

/ й! йО что (- > .

а% / й!

Таким образом, функция распределения по действию 1 должна удов­летворять уравнению Фоккера — Планка в виде

В дальнейшем нас будут интересовать лишь пролетные частицы. Ис­пользуя (20), для Б(1) можно получить простые выражения в двух пре­дельных случаях и &-*■ 1, т. е. в области прямолинейных траекторий,

И поблизости от сепаратрисы, разделяющий пролетные и захваченные тра­ектории. В первой из этих областей получаем

TOC o "1-5" h z Я(/)~б2/4/2. (50)

Если выполняется условие-^!» и;—Ц?{т) '>(±!'2юи то (50)

Аю йю I ’

переходит в (36). Чтобы убедиться в этом, необходимо в (36) разложить по малой разности ю—УУЫ), учесть, что в этой области 1~и, а также вспомнить определения и, т, б (см. раздел 16).

При &-И (1-^4/я) коэффициент диффузии расходится по логарифми­ческому закону

£>(/)~2я-Мб2|1п (/-4/я) |, (51)

А = J йх х2е~х (1+е~х)'

Где

О

Как и в предыдущем разделе, рассмотрим размытые распределения, эволюция которых определяется средним значением коэффициента диф­фузии Пм(и>). Для таких распределений поток I в пределах одной ячейки

У{™) <и;<И;+т> меняется на весьма малую величину ЫМж(<'[У+ —И7- )

(И^(т>)-1<1? и при приближенном описании процесса диффузия может считаться стационарной. Проанализируем процесс диффузии в области захваченных траекторий и;жЦ7{7П) (см. рис. 2). Предположим, что через эту область проходит некоторый поток. Пусть у какой-то частицы действие /по модулю уменьшилось до значения /<4/я, т. е. она захватилась вол­ной. Тогда в стационарном случае одновременно с этим другая частица должна перейти из захваченных в пролетные, ее действие должно возрасти. Таким образом, в области захваченных траекторий результирующий поток должен быть равен нулю, и эту область можно вообще не рассматривать.

В области пролетных траекторий переменную ю удобно заменить на /, поскольку при использовании последней уравнение диффузии принимает стандартный вид (49). Эта переменная при /»1 переходит в переменную

И, которая в свою очередь линейно связана с ю (см. раздел 16). Поэтому при /> 1 /(/) лишь нормировочным множителем отличается ОТ /(и>). Для

Определения АпДн?) достаточно знать разность)—{(]¥-т)) (см. раз­дел 26). Поскольку /(РР±(7И))>1, то для Оаг{ю) получаем следующее вы­ражение:

Г(И'<Г))

Оак(и>) = (№(]п)-'№(™))28(и(т)у1*( % (52)

Кк™.

Здесь знак ^ означает, что интегрирование идет только по пролетным: траекториям.

Частица быстро проходит через области, где коэффициент диффузии велик, и надолго задерживается там, где коэффициент диффузии мал. Поэтому значение Паь(м) должно определяться областями замедленной диффузии. Величина #(/) уменьшается с ростом /, т. е. с удалением от сепаратрисы, разделяющей области пролетных и захваченных траекторий.

Разделим область интегрирования в (52) на три части и оценим вклад

Каждой из них. К первой отнесем область значений /»1, именно она и

Определяет величину интеграла. Вклад второй, где /« 1 оказывается в

/ 5/1 4

(шъ&----- ) >1 раз меньше. Наконец, в третьей области (/-► ) коэф-

(1и? / к

Фициент диффузии логарифмически расходится. Расходимость вызвана неприменимостью метода последовательных приближений в окрестности сепаратрисы. Она должна устраниться при переходе к точной теории. Однако поскольку коэффициент диффузии стоит в знаменателе подын­тегрального выражения, то в любом варианте теории вклад этой области оказывается конечным и составляет малую долю порядка а2 от вклада вто­рой области. Таким образом, мы приходим к заключению, что Д»»(ш) оп­ределяется вкладом первой области. В ней траектории частиц близки к прямым линиям, и поэтому могут быть использованы все результаты, по­лученные в предыдущем разделе. В частности, коэффициент диффузии

(}& -*/*

Ш7,А---- ) <1 должен совпа­

Ло?/

Дать с (39).

В задаче о движении частиц в поле волны конечной амплитуды, кото­рая близка к рассматриваемой нами, вместо уравнения Фоккера — Планка используется кинетическое урвнение (см., например, [7]). Такой способ описания значительно сложнее, так как в кинетическое уравнение вхо­дит добавочная независимая переменная фаза. Нам удалось избавится от нее с помощью гамильтоновского формализма. Однако гамильтоновский формализм можно использовать далеко не всегда. Так, например, в него нельзя включать электрон-ионное трение, играющее существенную роль в задаче, рассматривавшейся в [7].

4. Самосогласованное рассмотрение

А) Решение волнового уравнения

В предыдущих разделах рассматривались колебания, для которых ус­ловие резонанса выполняется в центре ловушки ©==©«о. Если ©>©*о, то имеются две резонансные точки, симметрично расположенные относитель­но минимума магнитного поля[38]. За один период колебаний частица дваж­ды проходит через каждую из них. Естественно, что в этом случае ис­следование резонансного взаимодействия оказывается более сложным. Однако при ©>©#0 удается построить самосогласованное решение задачи, не считая поле электромагнитных колебаний заданным.

Покажем, как это делается. Рассмотрим колебания с круговой поляри­зацией, распространяющиеся вдоль магнитного поля, так называемые свисты. Они описываются уравнением

£Е+ /л уЕ+ <■»•'<* —£=о, (5з>

<1гг с 1 с2(со,(г)—со)

Где ©рв — электронная плазменная частота.

Предположим, что колебания Частоты © падают на ловушку слева (см. рис. 3). В этом случае справа от ловушки, т. е. в области г>1> коле­Бания будуТ распространяться слева направо. Соответствующее решение

Волнового уравнения (53) имеет вид

Ј<'>=e-,/T-l(a) exp (iq>(,)(z) )•

Здесь использованы обозначения к=и>/с, f=nB/k, a=l+iB/2k, в_ mr. zL.

Нормировочный множитель с е~т/4Г-1(а) введен для удобства дальнейших вычислений. Длина волны колебаний предполагается достаточно малой

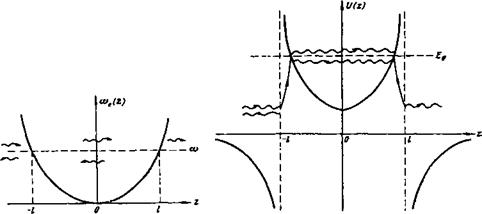
Рис. 3. Распространение циклотронных колебаний, падающих на адиабатическую ловушку. Направление распространения показано стрелками

Рис. 4. Циклотронные колебания приФо=2ял. Обозначения: £/0(г) =---------------------

С2 (©в (г)-©)

Полная энергия уравнения Шредингера.

Потенциальная энергия и Е0

Эквивалентного (53). Амплитуда колебаний в области прозрачности изображена вол­нистой линией

К1> 1, что делает возможным использование квазиклассического прибли­жения.

В области 12 11 <I уравнение (53) переходит в уравнение Уиттекера, а решение (54) принимает вид (см., например [15])

Я(г)-ЛГ (х) +<гт/Т-1 (2-а) У(х), (55)

Где Х— —2ik(z—l).

При х-^0 (г-+1) функция М регулярна М^х, а функция имеет ло­гарифмическую особенность И^«Г-1(а) (1+Вл;1пл;). Если решение задано справа от точки 2=1, то его вид при 2<1 будет зависеть от того, как мы продолжим решение через резонансную точку, т. е. определим неанали­тическую функцию 1п(г—/). Возможные правила продолжения логарифма имеют вид

1п (г—/) —*-1п12—^| — 1*я(1—а(г)). (56)

Здесь а(г) — произвольное число. При использовании правила обхода Лан­дау следует положить а(г)=0. Величина а(г) определяет скачок производ­ной при переходе через резонансную точку. С другой стороны, работа

Электрического поля волны над плазмой, производимая в резонансной точ­ке, дается выражением

7>а r! F I l+e Rr2

N = — E'(l)-~ — ——(1—a<r)) Е(I) Is. (57)

4ясо dz I i—Q 4 со

Таким образом, правило продолжения решения через резонансную точ­ку однозначно связано с долей энергии, поглощаемой в этой точке [8].

Оставим пока величину a(r) неопределенной. Тогда в области z<l решение (55) переходит в

TOC o "1-5" h z £<'>=—е-т/т-1 (2-a) W(х) + ( 1 - a(r) (1-е"т)) М(х). (58)

В квазиклассическом представлении оно имеет вид

Я<с)=етАГ-1 (a) ^ I _ J_ а(г> (1_е-т) ^ ехр (г<р(0' (г)) -

—ет/4Г_1(2—a) (l—^-a(r) Y(l—е_1,)ехр(—«p:c,(z)). (59)

Здесь ' 2 '

»'■’(z) (z+,)+ТкЫ{-ШТгУк 6'~2Ы ~т1“ш

Теперь продолжим решение (58), (59) через левую резонансную точку. Величина а{1 характеризующая правило продолжения, вообще говоря, может быть отлична от a(r). Процедура продолжения вполне аналогична использованной выше. В результате получаем

£<о=езТ//Т-1(2_а) _La<r>(i_e-T)

— ^1 —^_a<r> ) ^"а(!>) (1“е_т)2е'Ф°] ехр(гф(П (z)) +

+е_т/4 (1—е_1г)Г-1 (a) ^1--La(r)(i_e-T)

— ^1 + -^-а<0 (1—е~л)ел —^‘а(г> )е'Ф°] exP(—(z))- (60)

Здесь действительная величина

Ф.=2Ы-4In(Ш> + f, п [Г (1 - ".)/ Г (1 + -|)]

Имеет смысл набега фазы при распространении волны от одной резонан -

В / z—I 1

TOC o "1-5" h z спой точки до другой, cp(/)(z)=/c(;rH) + —In (----------------- ;---- —7 ).

2к z+l 4/а /

Для дальнейшего полезно также привести выражения для E(z) в ре­зонансных точках z= ±1

E(l)=r4 (61)

Е(-1)=ч~1ет(1-е-т) ^ 1 —~ а(т) (1—e-1r) j е~*ф°—

—(1 —V“(r>) (1—«-т)«<ф°] - (б2>

Полученные нами результаты позволяют найти коэффициенты погло­щения, отражения и прохождения колебаний[39]. Общие выражения громозд­ки, и поэтому мы рассмотрим простейшие предельные случаи. При

В область —I проникает экспоненциально малая часть энергии ~е~у. Игнорируя величины такого порядка малости, получаем, что падающая энергия частично поглощается с коэффициентом поглощения:

(63)

Остальная энергия отражается

(64)

Эти результаты справедливы, если выполняется условие | Ф0—2пп

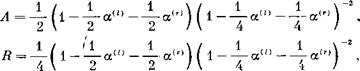В обратном случае Ф0~2:гт в ловушке устанавливаются колебания, напо­минающие собственные (см. рис. 4). Для иллюстрации пространственной зависимости таких колебаний удобно использовать аналогию волнового уравнения (53) с уравнением Шредингера [16 ]. В области прозрачности, где «энергия» Е0=((о/с)2 превышает «потенциал» С/0=—соре2со/с2(сое(2)—со), колебания имеют вид бегущих волн. Во внутренней области прозрачности имеются две волны, бегущие навстречу друг другу, причем амплитуда ко­лебаний, бегущих направо, превышает амплитуду колебаний, распростра­няющихся в обратном направлении (см. (59)). Внешняя область прозрач­ности отделена от внутренней плохо проницаемыми барьерами. В обла­стях непрозрачности амплитуда колебаний спадает экспоненциально, и по­этому наружу просачивается немного энергии. Соответственно немного энергии требуется и для поддержания стационарного уровня колебаний внутри ловушки. Все это приводит к^тому, что амплитуда колебаний при |г| >1 оказывается в е*/2 раз меньше, чем амплитуда колебаний внутри ловушки. Коэффициенты поглощения, отражения и прохождения в этом случае равны,

(65)

(65) (67)

Наконец, при ^<1 плазма оказывает малое влияние на распростране­ние колебаний. В этом случае почти вся энергия проходит через ловушку. Доля поглощаемой энергии имеет порядок 'у, отраженной у2.

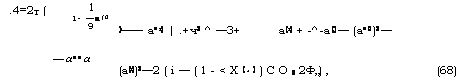Д=Тг(1-уа'Ч+1-(а<‘))г-а‘'>(1—^а^)с°з2ф.), (69)

Г=1+2к (—1 + -^-а<0+-^-а<г|) +к2 (2-~а(па(г> +

^ ш 9 & &

+ -|-(ч<,)),+о"'а(г,+ -|-(а(г,),+2(1-у«10) (1-у а'^созгФ.) .

(70)

Наша дальнейшая задача состоит в том, чтобы связать величины а(,) и а(г) с интенсивностью случайных воздействий, характеризуемой величи­ной р..Это будет сделано в следующем разделе.

Б) Вычисление коэффициентов а(1), а(г)

Будем отмечать индексом п число колебаний электрона по ловушке. Моменту прохождения левой резонансной точки при движении справа налево поставим в соответствие время после отражения от пробки электрон пройдет через эту точку слева направо в момент времени *пг. Правую резонансную точку электрон пройдет последовательно в момен­ты времени £*з, tn4. После прохождения через левую резонансную точку 1= —I дисперсия в значениях возрастает на величину

/)«>=0, =-^-< ш„)2- (ш„.4-ш») *>.

Здесь

Я

Ю»д—ШО=2Д<0ШоА V* (со. ч (а*,0 + соч (а»,2)) +

П

+2Д {г)и>? У^| (соз (аА, з) + соз(а*,4)); и>я+1Д—і0ов2Д(І)іі;оЛ (сое (ая+і, і) +

І

Е

.+ соз(а«+і,2)) +и? я,4—м;0; Д(,)(г)= —(Д£)Я (=РІ);

Т,

Д£ — время резонансного взаимодействия (см. раздел 1а)),

*-1

А»,і=ао+2(Дг—1)А(цр+Аі(ц?) + V (оі. і+Ш/.г+сйі. з+со/^+сОк. і;

І—і

2=а*, і+й2(м?) +©». г; а*. 3=а*. гКЗіМ+о*, Ф0; а*. 4=а*. з+^2(^)+сі)к, 4; фаза Ф0 была определена в предыдущем разделе; £2і(м>) набег фазы «

А (0 = | Л'(©,(*') — о) на траектории электрона между различными резо­нансными точками; &2(ш) — набег фазы между двумя последовательными прохождениями через одну и ту же точку; о*, і — набег фазы,

Вызванный случайными воздействиями, за интервал времени £*, 4—**-і, 4*,

Ю*. 2 за Ік, г—ІК 1 и т. д.

Усредняя (71) по статистическому ансамблю и производя суммирова­ние, получаем

/)(')=2и>(1—2p2cos 2Q+р4) [ (Д(,))2(1—(54- + (Рг—р4р2“4) cos Q.+ p2^*“1-^) cos (2Q—Q2)) +

(72)

+Д(0Д(г)(2рcos (Q—Фо)—2p3cos (Q+O0)+Picos (Qt—Ф0) —

—p4pi-1cos (Qt-f Ф0)+p2pi_1 cos (2Q—Qt—Ф0) + р2р1 cos (2Q—Qt—Ф0))]

Здесь pi=<cos (со* 1,з)>=е“0'*; p2=<cos cDfc; 2.4)>=e~0**; p=ptp2; a2=at2+a22; D{T) отличается от DU) заменами Ф0-»-—Фо, Д(г)->-Д(0, Д(,)->-Д(г).

Полученное нами выражение для коэффициента диффузии трудно обозримо. Мы продемонстрируем* общий ход рассуждений в пределе сла­бой корреляции р<1. Дополнительные упрощения связаны с ограниче­ниями, накладываемыми на величину у. Рассмотрим те же простейшие предельные случаи, что и в предыдущем разделе. Если |Фо—2яи|>

>е“7, то Е(—1)& — 2i^”1ev(l—^ а(О)зтФ0. Так как то в (72)

Мы можем опустить слагаемое, пропорциональное малому отношению

Д(г)/Д(0^е-7_

При этих предположениях выражение для коэффициента диффузии приобретает следующий вид:

D=Z)(,)+D<r>«2u;(A(,))2(l-2p*cos 2Q+^)-l(l-p+

(73)

+p2cosQ2+p2p2”1 cos (2Q—Q2)).

Это выражение содержит быстроосциллирующую составляющую. Про­изводя усреднение, аналогично тому, как это было сделано в разделе 2, получаем

Д»г=2ш(Д(0)2(1—р4), (74)

Fa.= ^-D„=2(A<")4i-p). (75)

Dw

Сила динамического трения (75) определяет среднее количество энер­гии, поглощаемой одной частицей в левой резонансной точке. Множитель два учитывает то обстоятельство, что за один период колебаний по ло­вушке частица дважды проходит через резонанс. Чтобы найти полное количество энергии, поглощаемое в точке z= —1Ч следует Fav помножить на число частиц, проходящих через эту точку в единицу времени г>ц/о(*>ц), и проинтегрировать по dvn. Поскольку (Д(,))а—^|Г* (см. раздел 1а)), то подынтегральное выражение не зависит от vh и мы приходим к (57) с заменой а(,) на р Такую же замену следует сделать и в выражениях для коэффициентов поглощения и отражения (63), (64). Из (63) следует естественный результат: коэффициент поглощения возрастает с уменьше­нием a(I)*=p4, т. е. с увеличением интенсивности случайных воздействий. Предельное значение А=1 (напомним, что вычисление ведутся с экспо­ненциальной точностью по параметру •у) достигается при р=0, когда при описании процесса резонансного взаимодействия можно использовать приближение хаотических фаз (см. раздел 2). В этом случае правило про­должения решения через резонансную точку совпадает с правилом обхода Ландау (см. (56)).

В другом простейшем предельном случае ^>1, |Ф0—2ял|<е~т анало­гичные вычисления дают

D*»4A2u?(14-p1 cos Qi+p*cos Q*), (76)

TOC o "1-5" h z Я..=4Дгш(1------- |(Я.*+fc*)), (77)

А, г)«а<'>*у(^+^). (78)

Наконец, при ^<1

/)«2Д2м> (2+2Я cos Qz+Яt cos (Qi—Ф0) +Яi cos (Qt+O0)), ‘(79)

£„»4Дгш (1—^-(Я,1 cos* Фо+рг2)) , (80)

Ew*a',>--i-(Я,1Coe,®.+Я,,). (81)

В двух последних предельных случаях Е(1) (см. (61), (62)), по­

Этому в (76), (77), (79), (80) Д(Г)«Д(,> = Д.

Найденные нами величины а(г), а(0, которые характеризуют правило продолжения решения через резонансные точки Z— ±/, следует подста­вить в выражения для коэффициентов отражения, поглощения и прохож­дения колебаний, полученные в предыдущем разделе.

Заключение

Таким образом, мы показали, что для нагрева плазмы в слабом элек­трическом поле ее необходимо подвергнуть случайным воздействиям. По лучены выражения для количества поглощаемой энергии в функции oi интенсивности случайных воздействий, характеризуемой величиной Я. При резонансе*фдали от минимума магнитного поля рассмотрено самосогласо­ванное волновое уравнение, описывающее распространение электромаг­нитных колебаний. Найдена связь между правилом продолжения решения через резонансную точку и величиной Я. Показано, что правило обхода Ландау предполагает полное отсутствие фазовой корреляции в моменты последовательного прохождения частицы через резонансную точку. Вы­числены коэффициенты отражения, поглощения и прохождения электро­магнитных колебаний, падающих извне на адиабатическую ловушку.

Автор благодарен С. В. Путвинскому за обсуясдение работы.

Институт атомной энергии