Постановка задачи. Основные уравнения
Допустим, что пространство между двумя коаксиальными цилиндрами радиуса и /?-*-</(</<^/?) заполнено слабононизованной плазмой. Предположим, что внутренний металлический цилиндр нагрет до такой температуры, что на его поверхности происходит термическая ионизация газа (например, паров цезия). Ионы и электроны, образованные на поверхности внутреннего цилиндра, амбиполярно диффундируют через нейтральный газ до внешнего цилиндра, где и происходит рекомбинация. Внешний цилиндр мы будем считать диэлектрическим, т. е. примем, что потоки электронов и ионов на него равны в каждой точке его поверхности.
Пусть в пространстве между цилиндрами имеется азимутальное магнитное поле, спадающее по радиусу, как. Это поле может быть
Создано, например, током, текущим по внутреннему цилиндру.
Учитывая, что плотность заряженных частиц значительно меньше, чем плотность нейтралов, считаем нейтральную компоненту неподвижной. Поведение заряженной компоненты описываем уравнениями непрерывности для электронов и ионов совместно с уравнениями движения.
Мы рассматриваем медленные колебания с частотой, много меньшей ленгмюровской. В этом случае плазму можно считать квазинейтральной, т. е. плотности электронов и ионов равными. Тогда уравнения непрерывности имеют следующий вид
Мы рассматриваем лишь азимутально симметричные движения. Из уравнения движения электронов
При условии, что. 1, получаем следующее выражение для попе
Речной по отношению к Н скорости
Аналогично для ионов имеем
^=71 {[Ь*е]-~£ [Ь Ц-]—^ V^"(Е)7 '^)• И)
Здесь ср — потенциал электрического поля; п — концентрация заряженных частиц; Н—величина магнитного поля; Л — единичный вектор,
Т х
Направленный вдоль магнитного поля; Ов = —*~*------- коэффициент диффу
Зии электронов; 6, = -^- — электронная подвижность; Тв — температура
О еИ
Электронов; тв — масса электрона; = — циклотронная частота
Электронов; — время между двумя последовательными соударениями электрона с нейтралами, аналогичные величины для ионов будем отмечать значком
Подставляя (3) и (4) в (1), получаем следующую систему из двух уравнений для определения п и <р
TOC o "1-5" h z Н дп ду дп__ дп_ ду _ 7 _1_ дп_ 1 Г_д_ / д<?
С дt ~дг дх дг дх е /? дг (2х)# |_ дх дх)~*
Д ( д<?- Т. 1 'Гд*п л
|
(5) |
![]() Дг П дг )] е (2т). |_ дх* дгг '
Дг П дг )] е (2т). |_ дх* дгг '
Н д<? дп дп ду 2 7*» 1 дп
С дt дг дх дг дх е /? дг (2т
В (5), пользуясь малой кривизной устройства, мы ввели локальную прямоугольную систему координат, направив ось £ вдоль оси цилиндров, ось У параллельно азимутальному магнитному полю и ось X от внешней поверхности к внутренней и взяв за начало координат произвольную точку на поверхности внешнего цилиндра. Эффекты, связанные с кривизной, давали малые поправки, и мы их не учитывали за исключением
Члена сИу, который в случае однородного поля равен нулю.
Если аксиальное поле меняется по радиусу как — , то он равен
0 1 дп /сч
~Н 7Г ~дг и пРеДставлен в уравнениях (5) третьим слагаемым.
Граничные условия находим из следующих соображений: поскольку плазма образуется на поверхности металлического цилиндра, плотность заряженной компоненты на внутренней границе считаем заданной и равной л0(</), на внешней, где происходит рекомбинация, полагаем ее равной нулю. Потенциал на поверхности металлического цилиндра также естественно положить равным нулю. В качестве четвертого граничного условия потребуем равенство электронного и ионного потоков на внешнюю диэлектрическую стенку.
В стационарном состоянии все величины зависят только от дг. Решая в этом предположении систему уравнений (5), получаем
|
П0(х) = п0{(1)^-, (•*•)__ 1 1 £ А - (3*0,- — (Зх), С1х X Ь, Ь{ (£2-:), ч-(Ст^ Для величины амбиполярного потока частиц нетрудно найти 1 с1по |
|
6,-»-6* с1х |
|
|||
|
|
||
|
Устойчивость плазмы исследуем, как обычно, с помощью линеаризованных уравнений для малых возмущений, причем возмущения плотности Лх и потенциала срх выбираем в виде /(х)ехр{—Ш-ь-Нег). Здесь и> — частота рассматриваемых колебаний; к — компонента волнового вектора вдоль оси Z. Для дальнейшего удобно взять линейные комбинации уравнений системы (5). В результате получаем следующую систему
С1щ) с1<ро дп
|
С1х дг с1х 1 (Т. Т{Гд*П1 (2т)# е е ) [_ дг1 дх1 J * . ( Т<___ Т±Ь.Г ^2. ^ "] Дt е е Ьв ) [_ с1х дг с/х дг J |
|
Для нахождения границы области устойчивости необходимо рассмотрение первой гармоники, так как при этом завибимость пг от координат наиболее плавная, и затухание, вызванное диффузией, будет наименьшим. Поскольку точное решение уравнений (7) затруднительно, естественно воспользоваться приближенным решением, аппроксимируя зависимость п1 от х какой-нибудь простой функцией. Примем приближенно, что лх = = />8тххехр {—/ш/-I-/£г}, где х = -^-. При этом из первого уравнения Системы (8) получаем Т Т Ь • т т • _______ (</по -11 ш Н п е ~ е Ь, 1 *!+»! < + ( 1 *1~ПА <1х ) | </х к с |
|
<* |
|
1 дпх Я дг |
|
X |
|
?г[- |
|
Я |
|
1_н Ьь. |
|
Ах |
|
(2х)# |
|
Очевидно, что при таком выборе зависимости от х граничные условия удовлетворяются. Действительно, П1 (0) = пх (</) = 0; ?!(</) = 0, |
|
|
|
|
 |
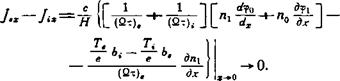
Дисперсионное уравнение получаем, подставляя выражение для <Рх во второе уравнение системы (8), умножая его на лх и интегрируя по х от 0 до cl. Для нахождения границы области устойчивости считаем действительной. Тогда, приравнивая по отдельности действительную и мнимую части дисперсионного уравнения, находим значение критического магнитного поля
Н2 = °2- 7t2 — (Q
6,6, d •
А также частоту раскачивающихся колебаний ш = 2k-jj '+у!" "
Интересно отметить, что соотношение (9) не содержит зависимости от температуры.
Условие (9) определяет Нс для первой гармоники с наибольшей длиной волной, для нее £ = х=-^-. Не для второй гармоники в два раза
Больше. При таких значениях //, когда неустойчива только первая гармоника, разовьется ламинарная конвекция в ячейках размером d. Более плотные участки плазмы будут выноситься наружу и гибнуть на стенке, внутрь будут идти участки с меньшей плотностью, в результате поток на внешнюю стенку возрастет.
Как и в случае обычной конвективной неустойчивости, это движение
Имеет дрейфовый характер и происходит со скоростью v = -^[hVcp].
Однако из-за соударений с нейтралами конвекционные движения будут связаны с диссипативными процессами.