ОБ ОДНОЙ СХЕМЕ ПРЯМОГО ПРЕОБРАЗОВАНИЯ ТЕПЛОВОЙ ЭНЕРГИИ ПЛАЗМЫ В ЭЛЕКТРИЧЕСКУЮ
А. В. ТИМОФЕЕВ
Ближайшей целью термоядерных исследований является демонстрация принципиальной возможности осуществления управляемой термоядерной реакции. Вопросам отвода энергии, вырабатываемой термоядерным реактором, уделяется пока еще мало внимания. Однако эти вопросы неизбежно приобретут актуальность, когда начнется практическое использование таких реакторов. Энергия, выделяющаяся при термоядерных реакциях, вообще говоря, распределяется между заряженными частицами и нейтронами. Ввиду высокой температуры плазмы практически вся тепловая энергия заряженных частиц может быть преобразована в электрическую. Разумеется, этого можно достигнуть лишь методами прямого преобразования без использования теплового цикла. Учитывая значение, которое начинают приобретать экологические вопросы, следует ожидать, что в будущем по мере развития физики и техники плазмы проявится тенденция к переходу на термоядерные реакции, протекающие без участия нейтронов. В этом случае удалось бы свести к минимуму как радиационное, так и тепловое загрязнение среды.
В любой схеме прямого преобразования заряженные частицы должны отдавать свою энергию, работая против внешнего электрического поля. При этом неизбежно встает вопрос, как обеспечить проникновение внешних электрических полей в плазму, преодолев стремление плазмы к их экранировке. В известной схеме прямого преобразования, предложенной Постом (см., например, [*]), предлагается снабдить термоядерный реактор вспомогательным устройством — экспандером (расширителем). В нем плазма, вытекающая из термоядерного реактора, расширяется настолько, что ее дебаевский радиус становится сравнимым с характерным размером устройства, осуществляющего отбор энергии. Расчеты показывают, что экспандер термоядерных реакторов должен иметь довольно большие размеры порядка 10* м (см., например, [*• *]).
В [3] была предложена иная схема прямого преобразования, по которой отбор энергии должен проводиться в скрещенных электрическом и магнитном полях. Присутствие магнитного поля, перпендикулярного электрическому, не позволяет зарядам перетекать вдоль электрического поля, что могло бы привести к уничтожению последнего. Чтобы создать в плазме электрическое поле, предполагается «закоротить» различные силовые линии магнитного поля на отдельные электроды достаточно малого размера, поддерживаемые при различных значениях электрического потенциала. Подробное описание устройства для прямого преобразования энергии (рекуператора), предложенного в [*], будет дано ниже. Такое описание и является целью настоящей работы.
В рассматриваемом рекуператоре не нужно предварительно расширять плазму, что позволяет избавиться от экспандера. Его устранение приводит к существенному (примерно на порядок величины) сокращению размеров всего рекуператора.
Первоначально проблема прямого преобразования (рекуперации) энергии рассматривалась лишь в связи с проектами термоядерных реакторов на основе открытых магнитных ловушек. Из-за больших потерь частиц через пробки открытых ловушек такие реакторы могут дать положительный выход лишь при условии рекуперации энергии. Вместе с тем в настоящее время обсуждается возможность подключения рекуператоров через дивер - торы к тороидальным системам (см., например, [4]).
1. Принцип действия
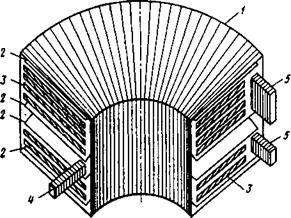
А. Преобразование энергии. В рассматриваемой схеме рекуперации тепловая энергия плазмы преобразуется в электрическую при дрейфе заряженных частиц в скрещенных полях: йеоднородном магнитном поле и перпендикулярном к нему электрическом. Проблема ввода плазмы в рекуператор будет обсуждаться ниже, пока же предположим, что плазма помещена в азимутальное магнитное поле, величина которого спадает по радиусу, и вертикальное электрическое поле. Такую комбинацию полей можно создать, например, с помощью плоской катушки, изображенной на рис. 1, внутри которой следует поместить обкладки конденсатора. Для определенности предположим, что верхняя обкладка заряжена положительно. Если направление магнитного поля таково, что заряженные частицы дрейфуют в скрещенных полях от центра системы, то они одновременно будут сдвигаться по вертикали, причем ионы — вверх, электроны — вниз. Этот вывод следует из уравнения дрейфового движения, которое удобно представить в виде (см., например, [5])
У-т[т (£)*]• <*>
Здесь ец=е—е<р(г) — ц#(г), ф(г) — потенциал электрического поля, Н(г) — магнитное поле, 1=г±/Н — магнитный момент, е — полная энергия частицы, значки «поперечно» и «продольно» отмечают направление относительно магнитного поля, которое считается безвихревым. Мы используем естественную цилиндрическую систему координат. Из (1) следует, что величина т^*=еи/Я2 при дрейфовом движении частицы должна оставаться постоянной. Из этого условия получаем
Е=е<р (г) +[1#(г) +т]Я2(г). (2)
Ти±ьг Н(г)
Здесь второе слагаемое дает энергию поперечного движения —----- ———,
2 Н (г0)
Ту,,» / Я (г) *
Третье — продольного-------- I -777—г-) . Поскольку полная энергия частицы
2 Н(га) /
Сохраняется, то дрейфовое движение в область меньшего магнитного поля должно сопровождаться переработкой тепловой энергии частицы в энергию электрического поля, причем продольная энергия перерабатывается эффективнее поперечной. Доля переработанной энергии (коэффициент рекуперации) р определяется отношением а (г) =* ■ ^ ^ и равна
Л (г0)
TOC o "1-5" h z р(г)=1-тха(г)-т„а!(г). (3)
Здесь обозначено —, тив----------- ——*
8Хо'"бцо вХо ' ®П0
б. Съем энергии. Выше мы считали магнитное поле в продольном направлении, т. е. по азимуту, однородным. Однако для того чтобы запереть заряженные частицы внутри катушки, следует на ее торцах увеличить магнитное поле, т. е. создать магнитные пробки. Этого легко добиться, увеличив плотность намотки вблизи торцов.
Магнитные пробки предполагается использовать для съема энергии. Не останавливаясь на деталях, которые будут подробно обсуждаться в дальнейшем, рассмотрим принцип съема энергии. Предполагается, что на небольшом расстоянии от магнитной пробки расположены секционированные по ОЯ и изолированные друг от друга электроды (см. рис. 1). Они должны занимать все сечение пробки плоскостью ЪОК. Предположим также, что электроны осуществляют хороший электрический контакт между плазмой и электродами. Явление электрического контакта плазмы, удерживаемой в
|
|
|
Рис. 1. Принципиальная схема устройства. 1 — катушка, создающая основное магнитное поле (обмотка показана тонкими линиями); 2 — Пластины конденсаторов; 3 - секционированные запробочные электроды (заштрихованы); 4 - система ввода плазмы; 5 - система вывода плазмы |
Адиабатической ловушке, с запробочными электродами принято называть «line-tying».Оно рассматривалось ранее главным образом в связи с проблемой стабилизации желобковой неустойчивости (см. [®], а также ниже). Если бы электроды были бесконечно тонкими по 02, а контакт идеальным, то потенциал каждого электрода совпадал бы с потенциалом опирающейся на него магнитной силовой линии.
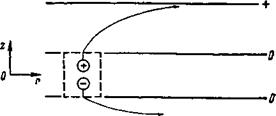
Принцип съема энергии иллюстрируется рис. 2 На нем изображено сечение рекуператора вертикальной плоскостью, проходящей через ось катушки. Заряженные частицы, поступающие из термоядерного реактора, дрейфуют в скрещенных полях слева направо. В положении 1 мы имеем нейтральную плазму. Из-за неоднородности магнитного поля ионы при дрейфе смещаются вверх, электроны — вниз (см. положение 2). Скорость дрейфа в неоднородном магнитном поле пропорциональна энергии заряженных частиц. При иллюстрации принципа действия рекуператора удобно считать энергию одной из компонент плазмы, например, электронов, пренебрежимо малой и соответственно пренебречь смещением электронов по вертикали. В положении 3 мы опять имеем нейтральную плазму, так как электроны перебросились посредством внешней цепи снизу вверх. Для этого необходимо, чтобы лишние электроны стекли через магнитную пробку на торцы в нижней части рекуператора, а затем были инжектированы в верхнюю. Поскольку при этом электроны будут перетекать от меньшего потенциала к большему, они могут совершать полезную работу. В результате всех этих процессов энергия электрического поля не меняется, энергия теплового движения ионов уменьшается на некоторую величину (см. (2)) и ровно столько же энергии отдается электронами во внешней цепи.
Практически для съема энергии следует каждый из электродов соединить через сопротивление с землей. Величппа сопротивления должна быть подобрапа таким образом, чтобы протекающий по нему ток создавал падение напряжения, равпое потенциалу электрического поля конденсатора
в месте нахождения электрода. Контакт между плазмой и электродами приводит к тому, что в плазме не может существовать нескомпенсирован - ный заряд. Поэтому плазма не будет влиять на распределение электрического поля внутри конденсатора. Следует отметить, что некоторые искажения потенциала, вообще говоря, допустимы. Важно лишь, чтобы не менял <2<р
Знака его градиент — , а вместе с ним и скорость дрейфа в скрещенных dz
Полях.
Обсудим влияние магнитных пробок на движение заряженных частиц. Неоднородность магнитного поля в области пробок вызывает дополнительный дрейф частиц по радиусу. Оценки показывают, что его скорость
|
! |
![]()
|
©©- |
![]() 0 г
0 г
' 2 3
Рис. 2. Принцип рекуперации энергии
Мала по сравнению со скоростью дрейфа в скрещенных полях, если вы-
Полняется услови* еФ>(е_1_еи) /* (~ ) (60)где Ф — полная разность потенциалов между обкладками конденсатора, к — расстояние между ними, 60 — угловой размер пробки.
Рассмотрим теперь вкратце системы, в которых в той или иной степени действуют те же физические процессы, что и в предлагаемом рекуператоре. Наиболее знакомы автору открытые магнитные ловушки. В таких ловушках совместное воздействие неоднородности магнитного поля и плотности плазмы приводит к раскачке желобковых колебаний, причем, как и в обсуждаемом рекуператоре,‘энергия плазмы передается колебаниям посредством дрейфа заряженных частиц в скрещенных полях (постоянном неод - нородном магнитном поле и перпепдикулярном к нему электрическом поле колебаний). При желобковой неустойчивости электрические поля создаются зарядами, выделяющимися на различных силовых линиях. Они могут быть нейтрализованы, а тем самым и стабилизирована желобковая неустойчивость, с помощью явления «Ипе-1у1^» (см., например, [“]).
Таким образом, в желобковых колебаниях проявляются физические процессы, которые лежат в основе как преобразования, так и съема энергии в рассматриваемом рекуператоре.
Для снятия зарядов, самопроизвольно возникающих в плазме, внешняя цепь использовалась также в экспериментах на токамаке [7] и плазменных ускорителях [•]. В [7] эксперименты проводились в условиях, когда вращательное преобразование было недостаточным для нейтрализации тороидального дрейфа. При этом тороидальный дрейф приводил к разделению зарядов, вызывавших электрическое поле, перпендикулярное магнитному. Для снятия поляризации плазменный шнур ограничивался металлическими пластинами, расположенными перпендикулярно оси токамака по обе стороны от шнура. Пластины соединялись проводником, расположенным вне камеры, по которому могли перетекать электрические заряды. Энергии тока было достаточно для того, чтобы поддерживать свечение небольшой электрической лампочки. Как и в рассматриваемом рекуператоре, энергия отбиралась из плазмы в результате дрейфа в скрещенных электрическом и неоднородном магнитных полях.
2. Некоторые проблемы
А. Устойчивость плазмы. В рассматриваемой системе при дрейфе плазмы по радиусу энергия продольного движения убывает быстрее поперечной е„/е_1=Я(г)/Я(го) (см. (2)). Тем самым создаются условия для раскачки так называемой анизотропной циклотронной неустойчивости (см., например, [®]). Основным результатом воздействия флуктуирующих электрических полей на плазму будет диффузия частиц в пространстве скоростей, которая должна уменьшать анизотропию функции распределения. При этом некоторые частицы могут выйти через пробки, унеся с собой нереку - перированную часть энергии. Однако возрастание продольной энергии частиц под действием циклотронных колебаний может иметь и положительный эффект. Действительно, энергия продольного движения частиц перерабатывается в электрическую быстрее поперечной, и поэтому при тех же размерах рекуператора эффективность рекуперации возрастет. Для этого параметры рекуператора следует подобрать таким образом, чтобы уменьшение анизотропии под действием циклотронных колебаний компенсировало ее увеличение в процессе рекуперации. К сожалению, современная теория циклотронных неустойчивостей не может дать вполне убедительных оценок величины коэффициентов турбулентной диффузии, поэтому вопрос о циклотронной неустойчивости, по-видимому, придется решать, основываясь на экспериментальных данных.
Что касается так называемой конусной неустойчивости, то она, по-видимому, не опасна для рассматриваемой системы. Действительно, эта неустойчивость будет развиваться лишь при выполнении условия (Ор^оц (см., например, [•]), в то время как оценки показывают (см. ниже), что плазма в рекуператоре характеризуется скорее обратным неравенством.
Обсудим теперь вопрос о желобковой неустойчивости. В рассматриваемой геометрии желобковая неустойчивость должна развиваться, если плотность плазмы спадает по радиусу быстрее чем 1/г[56]. Между тем из уравнения непрерывности для невозмущенной плазмы получаем и0(г)~1/г. Отсюда следует, что плазма в рекуператоре будет нечувствительной к же - лобковым возмущениям.
Б. Контакт плазмы с торцевыми электродами. Контакт плазмы с торцевыми электродами можно осуществлять двумя способами. Во-первых, для нейтрализации зарядов, выступающих в плазме, можно через пробки вдоль магнитного поля инжектировать заряды противоположного знака. Нейтрализация плазмы приводит к выравниванию потенциала вдоль силовой линии. При работе в стационарном режиме мы, вообще говоря, можем рассчитывать, какой ток следует инжектировать с каждого электрода. Если в качестве электродов взять подогревные катоды, то необходимая сила тока будет подбираться автоматически. Во-вторых, к горячей плазме можно добавить холодную. Так же как и горячая, она будет сноситься с дрейфовой скоростью по радиусу. Однако если заряженные частицы с большой энергией могут хорошо удерживаться пробками, то малоэнергичные частицы легко вытекают из ловушки под действием небольшого^ электрического потенциала. Поэтому когда горячие частицы смещаются по 02, то они вытесняют холодные вдоль магнитного поля на торцевые электроды. В этом методе «лишние» заряженные частицы отбираются из празмы. Разумеется, возможны и комбинации обоих методов. Так, например, можно отбирать электроны из той части системы, где выступают отрицательные заряды, и перебрасывать их туда, где выступают положительные.
«Закорачивание» зарядов, возникающих в плазме, через внешнюю цепь неизбежно ведет к потерям энергии. При инжекции энергия тратится на преодоление электрического поля пространственного заряда инжектируемых частиц. Минимальная разность потенциалов между электродом и плазмой определяется известным законом «трех вторых»:
Здесь I — расстояние между плазмой (пробками) и торцами, / — плотность инжектируемого тока.
Если для контакта с торцами использовать холодную плазму, то электрическое поле вытекающих зарядов компенсируется зарядами другого знака.
Оценим потери энергии при инжекции зарядов с торцевых электродов. Плотность тока, проходящего через магнитную пробку, дается приближенным выражением
|
(5) |
![]() ]&еп — Уи.
]&еп — Уи.
|
Здесь Ь — расстояние по азимуту между пробками рекуператора,
|
Мощность, затрачиваемая на инжекцию, равна И^/ср,/?&. Отношение к энергии частиц, поступающих в рекуператор в единицу времени.
|
|
|
Дается простой формулой |
(6)
Здесь, как и выше, Ф »Ек — полная разность потенциалов между обкладками конденсатора. Если по порядку величины еФ равно е0, то из (6) следует, что полный ток на торцевые электроды должен быть примерно равен эквивалентному току частиц, поступающих в рекуператор. Иными словами, каждый заряд должен примерно один раз проциркулировать по внешней цепи.
Потери энергии неизбежны также ввпду конечных размеров электродов по 02. Нетрудно сообразить, что если размер электрода бг, то доля теряемой энергии по порядку величины равна 6г/Я.
В. Ввод плазмы в рекуператор. Проблема ввода плазмы в рекуператор, по-видимому, будет решаться по-разному в зависимости от вида плазменной ловушки, используемой в термоядерном реакторе. Предположим, что для удержания плазмы используется открытая магнитная ловушка. Из открытой магнитной ловушки плазма вытекает по пучку магнитных силовых линий, проходящему через пробку. Этот пучок необходимо сопрячь с силовыми линиями магнитного поля рекуператора. Для сопряжения можно использовать дополнительную катушку, приставив ее к одному из торцов рекуператора (см. рис. 1). В конденсатор следует ввести две дополнительные обкладки, поддерживаемые при нулевом потенциале, расположив их таким образом, чтобы катушка ввода помещалась между ними. На рис. 3 изображено сечение рекуператора вертикальной плоскостью, проходящей через ось основной катушки. Поперечное сечение пучка магнитных силовых линий, по которому плазма входит в рекуператор, обозначено пунктиром. Внутрь конденсаторов заряженные частицы попадают через вырезы, сделанные в пластинах, прилегающих к пучку.
Частицы, вышедшие из открытой магнитной ловушки, движутся по отрезку магнитной силовой линии, заключенному между правой пробкой рекуператора и левой пробкой магнитной ловушки. Магнитное поле в этих
Пробках должно быть несколько большим магнитного поля в двух остальных пробках системы открытая ловушка — рекуператор. Неоднородность магнитного поля рекуператора приводит к дрейфу заряженных частиц в вертикальном направлении, причем ионы дрейфуют вверх, электроны — вниз. Предположим, что все частицы, покидающие открытую ловушку, попадают в рекуператор. Из условия равенства потоков электронов и ионов и выражения для скорости дрейфа в неоднородном магнитном поле следует Nlгi=n^г„ где Щ — плотность частиц сорта ;(е, г) в рекуператоре, е> — их средняя энергия. Поскольку обычно в открытой магнитной ловушке «10е„ то и.» Юл*. Для нейтрализации избыточного электронного заряда
|
Рио. 3. Движение заряженных частиц в рекуператоре |
В рекуператор должны быть добавлены низкоэнергичные ионы с плотностью Д*е«10Яі. Они не будут проникать в ловушку, так как должны отражаться положительным амбиполярным потенциалом, самопроизвольно устанавливающимся в таких системах.
До тех пор пока заряженные частицы не попали в область, занятую электрическим полем, они могут свободно перемещаться вдоль силовых линий магнитного поля из ловушки в рекуператор и обратно. За это время частицы успеют рассеяться на угол б^, по порядку величины равный б1Ь«(л^),А (здесь У І - частота соударений, И?*кі/Уві — Время дрейфа по области, свободной от электрического поля, Л| — высота этой области). Попав в пространство между пластинами конденсатора, частицы начинают уменьшать продольную энергию быстрее поперечной (см. выше). В результате угол т|> между скоростью частицы и магнитным полем возрастает
Гг *
По закону т|>—— и через некоторое время частицы захватываются в
Г0
Рекуператор, «отсекаясь» от открытой ловушки. Для эффективной работы рекуператора необходимо, чтобы время захвата не было слишком большим.
В области между пластинами конденсаторов преобразование энергии происходит способом, описанным выше. Отметим лишь, что в нижний конденсатор, в который поступают горячие электроны, должна быть добавлена холодная плазма. Низкоэнергичные электроны будут вытесняться на торцы при смещении горячих электронов по вертикали. Отметим, также, что холодная плазма будет дрейфовать только в радиальном направлении.
3. Сопоставление с рекуператором Поста
А. Рекуператор Поста. Довольно давно ведутся расчеты термоядерного реактора на основе открытой магнитной ловушки, дополненной рекуператором Поста. По-видимому, наиболее детально такой проект был разработан в [*]. В настоящем разделе мы вкратце опишем рекуператор Поста, при этом численные значения параметров будут браться из работы [2]. В следующем разделе рассчитаем, какими должны быть параметры предлагаемого рекуператора, если его использовать в проекте [*] вместо рекуператора Поста. Следует отметить, что в [*] была произведена совместная оптимизация системы ловушка — рекуператор. Поэтому использование рекуператора, предлагаемого нами, при других параметрах ловушки может оказаться более выгодным.
Рекуператор Поста состоит из двух основных частей: экспандера и коллектора. По форме экспандер близок к рекуператору, предлагаемому нами. Его горизонтальное сечение представляет собой сектор окружности
4
С углом раствора—л и радиусом 76 М. Высота экспандера равна 2 М.
О
Однако в отличие от нашего рекуператора в экспандере магнитное поле направлено не по азимуту, а по радиусу. В [2] рассчнтано, что из ловушки в рекуператор будет поступать поток плазмы интенсивностью «5-1021 частиц в Сек со средней энергией ионов «5-105 Эв. Энергия электронов не указывается, но, по-видимому, она должна быть примерно на порядок величины меньше. Максимальное магнитное поле в пробке ловушки равно
15 Т. При переходе от ловушки к рекуператору оно уменьшается вдвое до 7,5 Т. Частицы поступают в экспандер по пучку силовых линий магнитного поля прямоугольного сечения с размерами 1X4 М. В экспандере плазма, вытекающая из ловушки, попадает в плоский расширяющийся «веер» магнитных силовых линий. Двигаясь вдоль силовых линий магнитного поля, плазма расширяется, и ее плотность падает. Одновременно с этим энергия ларморовского вращения заряженных частиц переходит в энергию направленного движения вдоль магнитного поля. На выходе из рекуператора в поперечной степени свободы остается «1% первоначальной энергии. При максимальном значении радиуса магнитные силовые линии резким поворотом уводятся в сторону. По ним из плазмы удаляются электроны, отдавшие свою энергию амбиполярному электрическому полю. Оказавшиеся вне магнитного поля ионы попадают в электрическое поле, создаваемое рядом конденсаторов с последовательно повышающимся потенциалом (коллектор). Отдельный ион движется между пластин конденсаторов до тех пор, пока не отдаст большую часть своей энергии на работу против сил электрического поля. После этого он нейтрализуется на пластине конденсатора. Суммарные потери энергии в процессе рекуперации равны *30%. Они составляются из 5% потерь при вводе плазмы в рекуператор; 3,2% теряются на внутренних стойках, поддерживающих оболочку экспандера, 4,4% — на перезарядку и ионизацию; 1% на входе в коллектор и, наконец, 17% в самом коллекторе.
Б. Параметры предлагаемого рекуператора. Плазма в рекуператор поступает по пучку силовых линий магнитного поля, поперечные размеры которого равны 1X4 М. Со вторым из этих размеров связан начальный радиус г0, т. е. радиус, на который вводятся заряженные частицы. Примем, что средний радиус ввода г0=4 М, при этом Г0гшп=2 М, Г0тах=6 М. Если предположить, что потери при вводе в рекуператор и на торцах не превышают 10% (см. ниже), то на выходе из рекуператора допустимы потери в 20%. (При этом, как и в рекуператоре Поста, рассмотренном в предыдущем разделе, общие потери составят 30%.) У частиц, которые покидают открытую магнитную ловушку, в момент прохождения пробки почти вся энергия приходится на поперечную степень свободы. Предположим, что магнитное поле рекуператора при г=г0 т1„ близко к магнитному полю в пробке открытой ловушки и что поток плазмы распределен равномерно по пучку магнитных силовых линий, которым ловушка соединяется с рекуператором. При этом, принимая р=0,8 и используя (3), получаем, что максимальный радиус рекуператора должен быть равен «13 М. Ввиду малых размеров рекуператора он может поместиться внутри отдельного вакуумного модуля, конструкция которых разработана в [*]. В результате внутренние стойки оказываются не нужными. Потери на перезарядку и ионизацию пропорциональны объему плазмы. Поскольку объем предлагаемого рекуператора почти на два порядка меньше, чем объем рекуператора Поста, то соответствующие потери будут пренебрежимо малы.
V*, ни напряженность электрического поля равна 10е В/м и что расстояние между пластинами верхнего конденсатора равно 2 М. Если распределение ионов по энергиям является максвелловским, то при движении до максимального радиуса на верхней пластине погибнет менее 1% ионов, которые унесут с собой примерно такую же долю энергии. Расстояние между пластинами нижнего конденсатора, в который поступают электроны, может быть взято на порядок величины меньше, чем у верхнего. При выбранных значениях электрического и магнитного полей скорость дрей - СЕ
Фа VK=— На входе в рекуператор равна »104 М/Cert. При этом плотность
H.
Плазмы не превысит 1015 л-3, а безразмерное отношение будет удов-
Летворять условию—— <0,1. Следует отметить, что поскольку скорость
Дрейфа пропорциональна #-1~г, то при постоянном угле раствора рекуператора (мы принимаем его равным л) отношение не должно зависеть от радиуса. Энергия дрейфового движения на выходе из рекуператора составляет величину, меньшую 1% начальной энергии частиц.
Используя соотношение, полученное в конце раздела 2 в, можно показать, что ионы захватятся в рекуператор уже за один пролет по силовой линии, проходящей между пластинами верхнего конденсатора. Для захвата электронов потребуется большее число (порядка 10) пролетов.
Оценим теперь потери энергии на торцах. Энергетические затраты на инжекцию определяются выражениями (4) —(6). Из (5) находим плотность тока /«10"® А/мг. Если Z«10”Z Ж, то из (4) следует <ptД100 В, при этом в соответствии с (6) затраты на инжекцию будут пренебрежимо малы.
Выше отмечалось, что некоторые потери энергии будут связаны с секционированием электродов. Принимая, что размер электродов по OZ Равен »10-2 М, для соответствующих потерь получаем величину порядка 1%.
|
Рекуператоре. В [*] потери |
![]() Если в качестве электродов использовать подогревные катоды, то их функционирование будет сопряжено с расходом энергии на излучение. Нетрудно оценить, что при температуре электродов 1000° С (оксидированные катоды) на нагрев пойдет примерно 1% энергии, вырабатываемой в
Если в качестве электродов использовать подогревные катоды, то их функционирование будет сопряжено с расходом энергии на излучение. Нетрудно оценить, что при температуре электродов 1000° С (оксидированные катоды) на нагрев пойдет примерно 1% энергии, вырабатываемой в
На входе в рекуператор принимались равными 5%. Будем считать, что и в нашем случае мы имеем близкую величину.
Проведенное рассмотрение показывает, что оценка суммарных. потерь в 30% вполне реальна и, по-видимому, даже завышена. Таким образом, при радиусе в 13 л предлагаемый рекуператор будет работать с такой же эффективностью, как и стометровый рекуператор Поста.
За обсуждение работы автор благодарен И. Н. Головину и А. П. Поп - рядухину.
Институт атомной энергии Поступила в редакцию
Им. И. В. Курчатова 2 января 1978 г.
Литература
1. R. W. Moir, W. L. Barr, R. P. Freis, R. F. Post. Plasma Phys. and Contr. Nucl. Fusion
Research, v. 3, p. 315, IAEA, Vienna, 1971.
2. R. W. Werner, G. A. Carlson, J. Hovingh, J. D. Lee, M. A. Peterson. Preprint UCRL -
75054-2, 1973.
3. А. В. Тимофеев. Авт. свядет. № 2324515/25, от. 5.3.1976 г.
4. R. W. Moir, W. L. Barr. Nucl. Fusion, 13, 35, 1973.
5. Б. A. Трубников. Введение в теорию плазмы, ч. 1. М., МИФИ, 1969.
6. R. W. Moir, D. Е. Baldwin, G. A. Carlson, Т. К. Fowler, В. G. Logan, М. A. Lieber -
Man, L. D. Pearlstein, Т. C. Simonen. Preprint UCID-16736, 1975.
7. В. C. Муховатов. Plasma Phys. and Contr. Nucl. Fusion Research, v. 2, p. 577, IAEA,
Vienna, 1966.
8. В. Г. Падалка. В сб.: Физика и применение плазменных ускорптелей, под ред.
А. И. Морозова. Минск, «Наука и техника», 1974, стр. 199.
9. А. В. Тимофеев, В. И. Пистувович. В сб.: Вопросы теории плазмы, под ред. акад.
М. А. Леонтовпча, т. 5. М., Атомиздат, 1967, стр. 351.