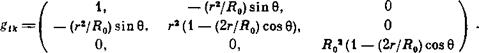ОБ АЛЬФВЕНОВСКОМ НАГРЕВЕ ПЛАЗМЫ В ОТКРЫТЫХ ЛОВУШКАХ
ТИМОФЕЕВ А. В.
1. В неоднородной плазме, помещенной в магнитное поле, альфвеновские колебания испытывают резонанс — поперечная по отношению к магнитному полю компонента показателя преломления (7УХ) обращается в бесконечность. Положение резонансной точки определяется условием лУцг=е, где — продольная компонента показателя преломления, е= = 1+й)р»2/(а),*—ю2), й)Р» — ионная ленгмюровская частота, ю» — ионная циклотронная частота. К выводу о бесконечных значениях N± приводит описание альфвеновских колебаний в приближении одножидкостной гидродинамики. Более детализированное рассмотрение показывает, что в окрестности резонансной точки альфвеновские колебания трансформируются в коротковолновые потенциальные, которые затем поглощаются электронами. На этом принципе основан так называемый альфвеновский нагрев плазмы (см., например, [1, 2]).
Анализируя пригодность альфвеновского нагрева для открытых ловушек, мы сталкиваемся с трудностью, обусловленной ограниченностью открытых ловушек в направлении вдоль магнитного поля. Дело в том, что возрастание при подходе волнового пакета к резонансной поверхности сопровождается резким уменьшением поперечной компоненты групповой скорости. В результате траектория волнового пакета как бы выстилается вдоль резонансной поверхности*. Если система ограничена вдоль силовых линий магнитного поля, то альфвеновские колебания, смещаясь вдоль резонансной поверхности, могут выйти из нее, не испытав резонанса (не трансформировавшись в коротковолновые потенциальные). Следует также отметить, что при движении по двумерно-неоднородной плаяме, какой является плазма открытых ловушек, не остается постоянной и Вместе с последней величиной меняется положение резонансной поверхности. Заранее не ясно, останется ли она в пределах досягаемости пакета.
В настоящей работе показано, что для альфвеновского нагрева предпочтительны открытые ловушки, в достаточной степени вытянутые вдоль магнитного поля. В коротких ловушках ВЧ энергия может быть затрачена на нагрев разреженной периферийной плазмы. Такие трудности не возникают в замкнутых ловушках, не имеющих торцов. Характерные особенности распространения альфвеновских колебаний в замкнутой ловушке (токамаке) иллюстрируются в настоящей работе отдельным примером.
2. Для нагрева плазмы оптимально использовать колебания с поперечной длиной волны, сравнимой с размером плазмы, которые достаточно эффективно связаны с ВЧ антеннами. Такие колебания находятся на границе области применимости квазиклассического приближения. Однако, поскольку квазиклассика «хорошо работает» и в этом случае, будем использовать ее в настоящей работе.
Рассмотрим сначала вопрос приближенно — аналитически. Квазиклас - сическое дисперсионное уравнение альфвеновских колебаний, как известно (см., например, [1,2]), имеет вид
0-ЛГх*(Лу-е)+(ЛГ,*-е)*- (в—1)*(—)*— 0. (1)
' А); •
1 Аналогичный вид могут иметь траектории волновых пакетов вблизи поверх* пости плазменного резонанса [3].
Проанализируем распространение альфвеновских колебаний в малой области пространства, где зависимость плотности от координат можно считать линейной: По(г)=По(0) (i—xlL±—Z/L„). Здесь Х — координата поперек магнитного поля, Z — вдоль. Магнитное поле будем для простоты считать однородным. Предположим, что поперечная компонента показателя преломления достаточно велика: iV±*»iV„2~e. В этом случае из (1) получаем следующую систему уравнений, задающих траекторию волнового пакета в параметрической форме:
|
(2) |
![]() Б*-2^№—е), T*-2ад,
Б*-2^№—е), T*-2ад,
Tfx»JVx! e (0 )IL± (0 )/£„'.
Здесь для упрощения анализа время г заменено безразмерным параметром т, осуществляющим параметризацию траектории (с^т=с2£/д/)/да)(г(г)г N(0)- Можно показать, что с ростом времени параметр т уменьшается. В (2) введены безразмерные величины |=(ох/с, ^—юг/с, Ь±=ыЬх1с,
L\ —ы)Lj|/c.
Из третьего уравнения системы (2) находим, что N±<0 и возрастает по модулю —Ь±'1(е (0)т). Поэтому, как следует из (1), по мере распространения пакета разность ^ц2—е должна уменьшаться. Последнее уравнение системы (2) показывает, что уменьшается и продольная составляющая показателя преломления А^1( (х) =Л^ц (то) + (£а'2/£ц'е(0))Х Х(1/то—1/т), поэтому пакет должен смещаться вдоль магнитного поля к границе плазмы. В соответствии с первым уравнением системы (2) его смещение поперек силовых линий магнитного поля оказывается существенно меньшим.
Из выражения для ^ц(т) можно оценить значение тт<п, при котором существенно падает по величине, и поэтому в соответствии со сказанным выше пакет подходит к границе плазмы Ттхп~Ь±гЩ'еЛ^10. За это время N± достигает значения М±тах~(Ц'/Ь±')Мц{То).
Обсудим теперь вопрос о реализации альфвеновского резонанса в открытых ловушках. Как отмечено выше, при резонансе альфвеновские колебания трансформируются в колебания с существенно меньшим пространственным масштабом, которые затем поглощаются электронами. В процессе трансформации поперечный показатель преломления альфвеновских колебаний достигает значений (вц/агде 8ц — продольная компонента диэлектрической проницаемости, сс= 1—р» (377г1-/2/7ге) Зсо»2/
/(4а)г2—а)2), р*=8лРг/В2, Р{ — давление ионов [1,2,4]. Естественно считать, что процесс трансформации действительно имеет место, если Тах Окажется сравнимым с (ен/а//)7* или большим этой величины. Данное условие можно представить в виде
Здесь использована оценка (то)'^7’.
Условие (3) показывает, что альфвеновский резонанс реализуется лишь в системах, в достаточной степени вытянутых вдоль магнитного поля. При о)~а), и параметрах плазмы, характерных для современных открытых ловушек, из условия (3) получаем 10. Если параметры
Плазмы не удовлетворяют условию (3), то ВЧ энергия затрачивается на нагрев разреженной плазмы в районе пробок или в запробочной области. Отметим, что обычно в промежутке от пробок до стенок камеры магнитное поле существенно падает. Поэтому, если частота колебаний, используемых для нагрева, не слишком мала, возникает конфигурация «магнитного берега», в которой альфвеновские колебания поглощаются с высокой эффективностью. (Разумеется, если до точки циклотронного резонанса они не трансформируются в потенциальные электронные.)
3. Изложим теперь результаты численного анализа распространения альфвеновских колебаний в открытых ловушках. Магнитное поле ловушки
X(r)-V(*)-(rV4)V"(*), где F=(V2) ((Я-f l)z—(У31„/я) (/?—1) sin (nz/y3L|,)), R — пробочное от
Ношение. Это представление справедливо для приосевой области. В расчетах принималось R=2. Предполагалось, что плотность плазмы распределена по закону Па(т)=по(0) exp (— (R/L±)2— (г/£ц)2), где L„=aL±. Параметр А определяет степень вытянутостп плазмы вдоль оси ловушки. Плазма современных открытых ловушек характеризуется соотношением a)pi> >o)t. В этом случае, нормируя N на a)Pi(0)/a)<(0), можно исключить из дисперсионного соотношения (1) абсолютные значения плотности плазмы и магнитного поля. В расчетах принималось (со/сог(0))2=0,5.
Интегрировались уравнения движения волнового пакета
Г—(с/ю) (DD№)/{dD/d(o), Ti=(clu)(dDldT)l(dDlda).
Счет прекращался, когда на траектории пакета плотность плазмы становилась равной 0,1 от плотности в центре ловушки.
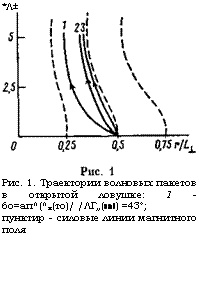
Характерные особенности траектории волновых пакетов можно видеть на рис. 1. Результаты расчетов подтверждают представления, сформулированные в предыдущем пункте. Так, подтверждается вывод о монотонном возрастании NСтепень близости к альфвеновскому резонансу естественно характеризовать величиной N На траектории пакетов она меняется весьма значительно. По мере ее роста траектории вытягиваются вдоль силовых линий магнитного поля. Если велико начальное значение УУ±, то практически вся траектория близка к силовой линии магнитного поля.
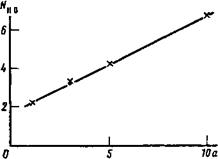
Расчеты траекторий при различных значениях параметра А=Ц]/Ь± позволили построить зависимость Л^±твае от А (рис. 2). В соответствии с предыдущим пунктом она близка к линейной, хотя коэффициент пропорциональности оказывается в ~2 раза меньшим:
Dlda{N±mJNt(T.))*>0№.
4. Нагрев плазмы с помощью альфвеновских колебаний предпочтительно осуществлять в замкнутых ловушках. Действительно, в системах с замкнутыми силовыми линиями магнитного поля ничто не мешает процессу приближения пакета альфвеновских колебаний к состоянию резонанса. Его траектория, вытягиваясь вдоль силовой линии магнитного поля, должна вместе с ней заполнить магнитную поверхность. (Разумеется, если прежде альфвеновские колебания не трансформируются в потенциальные) . Этот вывод соответствует результатам работ [5, 6], где утверждалось, что в токамаках альфвеновские колебания испытывают резонанс на магнитной поверхности.
Распространение альфвеновских колебаний в тороидальной плазме рассматривалось с помощью уравнений
І‘=-(с/to) (dD/dNi)l(dD/da), (dDldx^KdD/dv).
|
Здесь Х* — контравариантные координаты радиус-вектора, — малый Радиус, х2=0 — полоидалБный угол, х3=ф — тороидальный угол, N^ — ко - вариантные компоненты показателя преломления. Метрический тензор был взят из [7]:
|
Принималось, что проекции магнитных поверхностей на плоскость Ф=сопз1 имеют вид концентрических окружностей: ^=*0, В9=(Во*/г)Х X (1 + (2г//?0) соз 0), (2?0ф/Яо) (1+ (2г//?0) соз 0), 2?0Ф—32?<Л Распреде -
|
|
|
*Л± Рис. 1. Траектории волновых пакетов в открытой ловушке: 1 - 6о=ап^(^х(то)/ /ЛГ„(то)) =43°; 2 - 00=57°; 3 - 0О=72°; Пунктир - силовые линии магнитного поля |
|
Рис. 2 |
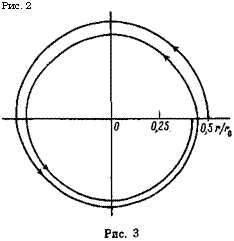 Рис. 2. Зависимость тах№(То) ОТ длины ловушки (по результатам расчета траекторий волновых пакетов, стартовавших в медианной плоскости ловушки при Г/£±=0,5, 00=57°)
Рис. 2. Зависимость тах№(То) ОТ длины ловушки (по результатам расчета траекторий волновых пакетов, стартовавших в медианной плоскости ловушки при Г/£±=0,5, 00=57°)
Рис. 3. Траектория волнового пакета в то - камаке, стартовавшего в точке г=г0, 0=0 при ЛГгШ^ОІ/Шріф) =*0,19, ЛГв=0, ЛГфсй{(0)/ /й)р,(0) =1,43
Ление плотности плазмы выбиралось в виде По(т)=по(0) ехр (— (г/г0)[84]), где г0=/?о/3. Одна из характерных траекторий альфвеновских колебании с о)=а),(0)/У2 изображена на рис. 3. В соответствии с высказанными выше соображениями она имеет вид спирали, накручивающейся на окружность r=const.
В заключение отметим, что в настоящей работе рассматривался только нагрев с помощью альфвеновских колебаний. В другом варианте альфвеновского нагрева антенна возбуждает магнитозвуковые колебания, которые просачиваются через область непрозрачности к точке альфвеновского резонанса, где трансформируются в коротковолновые потенциальные. Такую схему нагрева разумно использовать при малых значениях волнового числа альфвеновских колебаний (приближение, обратное ква - зиклассическому), и она, по-видимому, может быть осуществлена в более коротких открытых ловушках.
За обсуждение работы автор благодарен В. JI. Вдовину и А. В. Звонкову.
|
Поступила в редакцию 17.XI.1987 |
![]()
|
Институт атомной энергии им. И. В. Курчатова |
![]() Литература
Литература
|
Том 14 |
![]()
|
Вып. 10 |
![]()
|
ФИЗИКА ПЛАЗМЫ 1988 |
![]() УДК 533.951.8
УДК 533.951.8